1.3 Linear Functions
In Section 1.1.2, we concerned ourselves with the finite line segment between two points [latex]P[/latex] and [latex]Q.[/latex] Specifically, we found its length (the distance between [latex]P[/latex] and [latex]Q[/latex]) and its midpoint. In this section, our focus will be on the entire line, and ways to describe it algebraically. Consider the generic situation below.
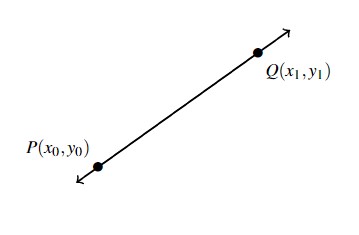
To give a sense of the steepness of the line, we recall that we can compute the slope of the line as follows. (Read the character [latex]\Delta[/latex] as change in.)
A couple of notes about Equation 1.3 are in order. First, don’t ask why we use the letter [latex]m[/latex] to represent slope. There are many explanations out there, but apparently no one really knows for sure.[1] Secondly, the stipulation [latex]x_{1} \neq x_{0}[/latex] (or [latex]\Delta x \neq 0[/latex]) ensures that we aren’t trying to divide by zero. The reader is invited to pause to think about what is happening geometrically when the change in [latex]x[/latex] is 0; the anxious reader can skip along to the next example.
Example 1.3.1
Example 1.3.1.1
Compute the slope of the line containing the following pairs of points, if it exists. Plot each pair of points and the line containing them.
[latex]P(0,0), \; Q(2,4)[/latex]
Solution:
In each of these examples, we apply the slope formula, Equation 1.3.
Compute the slope of the line containing the points [latex]P(0,0)[/latex] and [latex]Q(2,4),[/latex] if it exists.
\[ \begin{array}{rcl} m &=& \dfrac{4 – 0}{2 – 0}\\ & & \\ &=& \dfrac{4}{2} \\ & & \\ &=& 2 \\ \end{array} \]
Plot the pair of points and the line containing them.
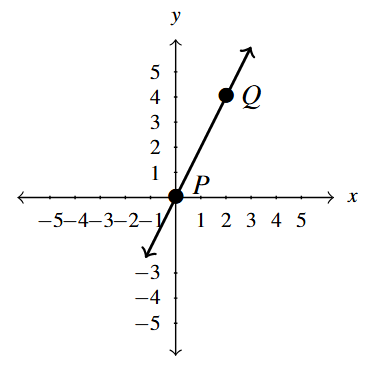
Example 1.3.1.2
Compute the slope of the line containing the following pairs of points, if it exists. Plot each pair of points and the line containing them.
[latex]P(-1,2), \; Q(3,4)[/latex]
Solution:
In each of these examples, we apply the slope formula, Equation 1.3.
Compute the slope of the line containing the points [latex]P(-1,2)[/latex] and [latex]Q(3,4),[/latex] if it exists.
\[ \begin{array}{rcl} m &=& \dfrac{4 – 2}{3 – (-1)} \\ & & \\ &=& \dfrac{2}{4} \\ & & \\ &=& \dfrac{1}{2} \\ \end{array} \]
Plot the pair of points and the line containing them.
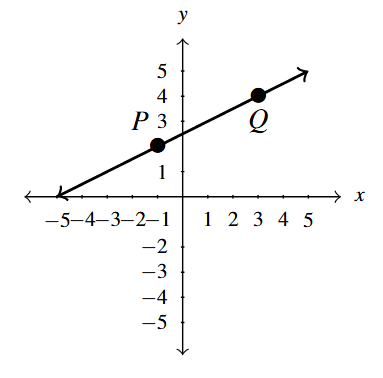
Example 1.3.1.3
Compute the slope of the line containing the following pairs of points, if it exists. Plot each pair of points and the line containing them.
[latex]P(-2,3), \; Q(2,-3)[/latex]
Solution:
In each of these examples, we apply the slope formula, Equation 1.3.
Compute the slope of the line containing the points [latex]P(-2,3)[/latex] and [latex]Q(2,-3)[/latex], if it exists.
\[ \begin{array}{rcl} m &=& \dfrac{-3 – 3}{2 – (-2)} \\ & & \\ &=& \dfrac{-6}{4} \\ & & \\ &=& -\dfrac{3}{2} \\ \end{array} \]
Plot the pair of points and the line containing them.
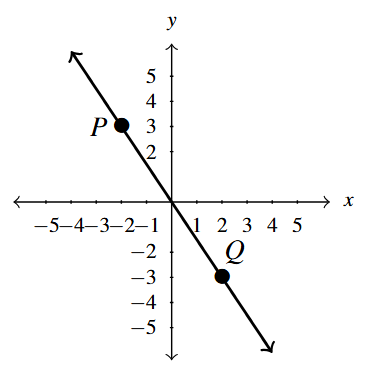
Example 1.3.1.4
Compute the slope of the line containing the following pairs of points, if it exists. Plot each pair of points and the line containing them.
[latex]P(-3,2), \; Q(4,2)[/latex]
Solution:
In each of these examples, we apply the slope formula, Equation 1.3.
Compute the slope of the line containing the points [latex]P(-3,2)[/latex] and [latex]Q(4,2)[/latex], if it exists.
\[ \begin{array}{rcl} m &=& \dfrac{2 – 2}{4 – (-3)} \\ & & \\ &=& \dfrac{0}{7} \\ & & \\ &=& 0 \\ \end{array} \]
Plot the pair of points and the line containing them.
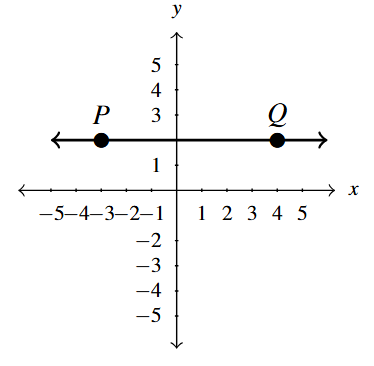
Example 1.3.1.5
Compute the slope of the line containing the following pairs of points, if it exists. Plot each pair of points and the line containing them.
[latex]P(2,3), \; Q(2,-1)[/latex]
Solution:
In each of these examples, we apply the slope formula, Equation 1.3.
Compute the slope of the line containing the points [latex]P(2,3)[/latex] and [latex]Q(2,-1),[/latex] if it exists.
\[ \begin{array}{rcl} m &=& \dfrac{-1 – 3}{2 – 2} \\& & \\ &=& \dfrac{-4}{0}, \text{ which is undefined} \\ & & \\ & \; & \; \\ \end{array} \]
Plot the pair of points and the line containing them.
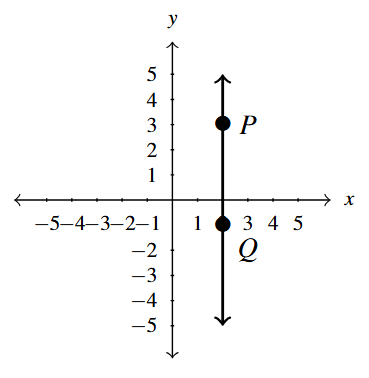
Example 1.3.1.6
Compute the slope of the line containing the following pairs of points, if it exists. Plot each pair of points and the line containing them.
[latex]P(2,3), \; Q(2.1, -1)[/latex]
Solution:
In each of these examples, we apply the slope formula, Equation 1.3.
Compute the slope of the line containing the points [latex]P(2,3)[/latex] and [latex]Q(2.1, -1)[/latex], if it exists.
\[ \begin{array}{rcl} m &=& \dfrac{-1 – 3}{2.1 – 2} \\ & & \\ &=& \dfrac{-4}{0.1} \\ & & \\ &=& -40 \\ \end{array} \]
Plot the pair of points and the line containing them.
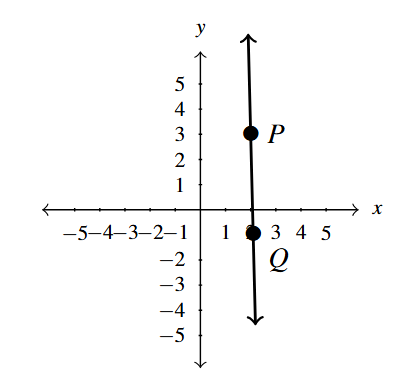
A few comments about Example 1.3.1 are in order. First, if the slope is positive then the resulting line is said to be increasing, meaning as we move from left to right,[2] the [latex]y[/latex]-values are getting larger. Similarly, if the slope is negative, we say the line is decreasing, for as we move from left to right, the [latex]y[/latex]-values are getting smaller. A slope of 0 results in a horizontal line which we say is constant, as the [latex]y[/latex]-values here remain unchanged when we move from left to right, and an undefined slope results in a vertical line.[3]
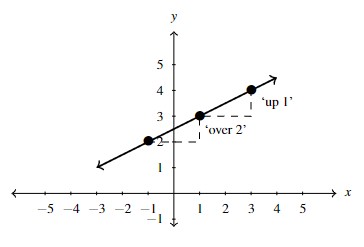
Second, the larger the slope is in absolute value, the steeper the line. You may recall from Algebra that slope can be described as the ratio [latex]\dfrac{rise}{run}.[/latex] For example, if the slope works out to be [latex]\dfrac{1}{2},[/latex] we can interpret this as a rise of 1 unit upward for every run of 2 units to the right:
In this way, we may view the slope as the rate of change of [latex]y[/latex] with respect to [latex]x.[/latex] From the expression
\[ m = \dfrac{\Delta y}{\Delta x}\]
we get [latex]\Delta y = m \cdot \Delta x[/latex] so that the [latex]y[/latex]-values change [latex]m[/latex] times as fast as the [latex]x[/latex]-values. We’ll have more to say about this concept when we explore applications of linear functions; presently, we will keep our attention focused on the analytic geometry of lines. To that end, our next task is to find algebraic equations that describe lines and we start with a discussion of vertical and horizontal lines.
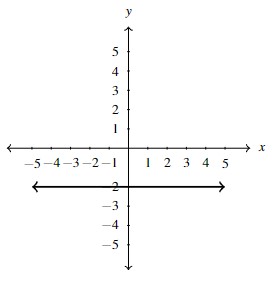
Consider the two lines shown below: [latex]V[/latex] (for Vertical Line) and [latex]H[/latex] (for Horizontal Line).
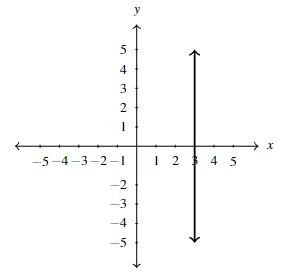
All of the points on the line [latex]V[/latex] have an [latex]x[/latex]-coordinate of 3. Conversely, any point with an [latex]x[/latex]-coordinate of 3 lies on the line [latex]V[/latex]. Said differently, the point [latex](x,y)[/latex] lies on [latex]V[/latex] if and only if [latex]x = 3.[/latex] Because of this, we say the equation [latex]x=3[/latex] describes the line [latex]V,[/latex] or, said differently, the graph of the equation [latex]x=3[/latex] is the line [latex]V.[/latex]
Turning our attention to [latex]H,[/latex] we note that every point on [latex]H[/latex] has a [latex]y[/latex]-coordinate of [latex]-2,[/latex] and vice-versa. Hence the equation [latex]y = -2[/latex] describes the line [latex]H,[/latex] or the graph of the equation [latex]y=-2[/latex] is [latex]H.[/latex] In general:
Equation 1.4 Equations of Vertical and Horizontal Lines
- The graph of the equation [latex]x = a[/latex] in the [latex]xy[/latex]-plane is a vertical line through [latex](a, 0).[/latex]
- The graph of the equation [latex]y = b[/latex] in the[latex]xy[/latex]-plane is a horizontal line through [latex](0, b).[/latex]
Of course, we may be working on axes which aren’t labeled with the usual [latex]x[/latex]‘s and [latex]y[/latex]‘s. In this case, we understand Equation 1.4 to say horizontal axis label [latex]= a[/latex] describes a vertical line through [latex](a,0)[/latex] and vertical axis label [latex]= b[/latex] describes a horizontal line through [latex](0,b).[/latex]
Example 1.3.2
Example 1.3.2.1a
Graph the following equations in the [latex]xy[/latex]-plane:
[latex]y = 3[/latex]
Solution:
Graph [latex]y=3[/latex] on the [latex]xy[/latex]-plane.
By now we’re familiar with the [latex]xy[/latex]-plane, the graph of [latex]y=3[/latex] is a horizontal line through [latex](0,3),[/latex] shown below.
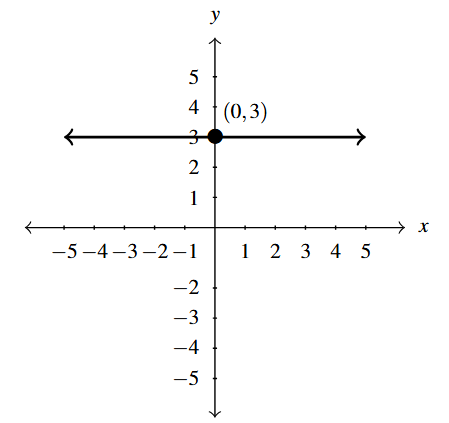
Example 1.3.2.1b
Graph the following equations in the [latex]xy[/latex]-plane:
[latex]x=-117[/latex]
Solution:
Graph [latex]x=117[/latex] on the [latex]xy[/latex]-plane.
By now we’re familiar with the [latex]xy[/latex]-plane, the graph of [latex]x = -117[/latex] is a vertical line through (-117, 0). We scale the [latex]x[/latex]-axis differently than the [latex]y[/latex]-axis to produce the graph below.
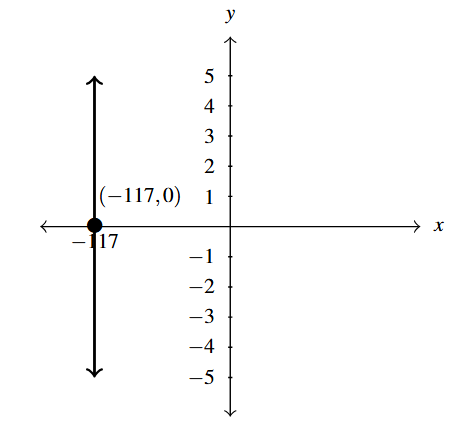
Example 1.3.2.2
Write the equation of each of the given lines.
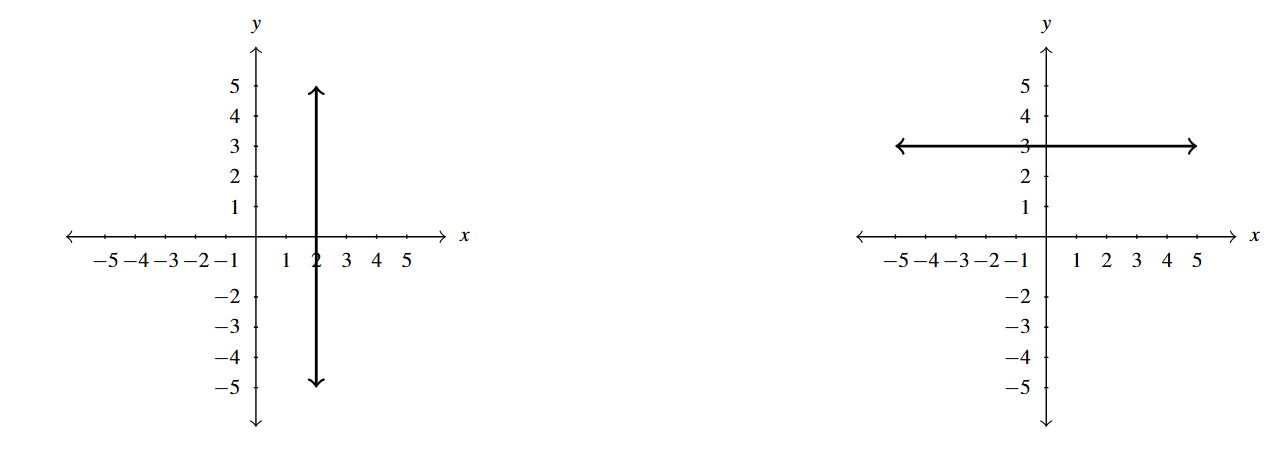
Solution:
[latex]L_{1}[/latex] is a vertical line through [latex](2,0),[/latex] and the horizontal axis is labeled with [latex]x,[/latex] thus the equation of [latex]L_{1}[/latex] is [latex]x = 2.[/latex]
[latex]L_{2}[/latex] is a horizontal line through [latex](0,3)[/latex] and the vertical axis is labeled as [latex]y,[/latex] therefore the equation of this line is [latex]y= 3.[/latex]
Using the concept of slope, we can develop equations for the other varieties of lines. Suppose a line has a slope of [latex]m[/latex] and contains the point [latex]\left(x_{0}, y_{0}\right).[/latex] Suppose [latex](x,y)[/latex] is another point on the line, as indicated below.
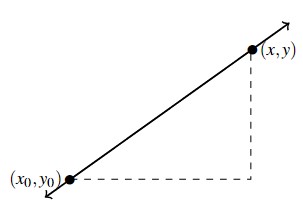
Equation 1.3 then yields
\[ \begin{array}{rclr}
m & = & \dfrac{y – y_{0}}{x-x_{0}} & \\
m\left(x – x_{0}\right) & = & y – y_{0} & \\
y – y_{0} & = & m\left(x – x_{0}\right) & \\
\end{array} \]
which is known as the point-slope form of a line.
Equation 1.5
The point-slope form of the line with slope [latex]m[/latex] containing the point [latex]\left(x_{0}, y_{0}\right)[/latex] is the equation
\[y – y_{0} = m\left(x – x_{0}\right)\]
A few remarks about Equation 1.5 are in order. First, note that if the slope [latex]m = 0,[/latex] then the line is horizontal and Equation 1.5 reduces to [latex]y - y_{0} = 0[/latex] or [latex]y = y_{0},[/latex] as prescribed by Equation 1.4.[4] Second, we may need to change the letters in Equation 1.5 from [latex]x[/latex] and [latex]y[/latex] depending on the context, so while Equation 1.5 should be committed to memory, it should be understood that [latex]x[/latex] refers to whichever variable is used to label the horizontal axis, and [latex]y[/latex] refers to whichever variable is used to label the vertical axis. Lastly, while Equation 1.5 is, by far, the easiest way to construct the equation of a line given a point and a slope, more often than not, the equation is solved for [latex]y[/latex] and simplified into the form below.
The slope-intercept form of the line with slope [latex]m[/latex] and [latex]y[/latex]-intercept [latex](0,b)[/latex] is the equation \[y = mx + b\]
Equation 1.6 is probably[5] a familiar sight from High School Algebra. You may recall that the intercept in slope-intercept comes from the fact that this line intercepts or crosses the [latex]y[/latex]-axis at the point [latex](0,b)[/latex].[6] If we set the slope, [latex]m = 0[latex], we obtain [latex]y=b[latex], the formula for Horizontal Lines first introduced in Equation 1.4. Hence, any line which has a defined slope [latex]m[latex] can be represented in both point-slope and slope-intercept forms. The only exceptions are vertical lines which do not have a defined slope. There is one equation - the aptly named general form - which describes every type of line, including vertical lines, and it is presented below.
Note the indefinite article a in Equation 1.7. The line [latex]y = 5[/latex] is a general form for the horizontal line through [latex](0,5)[/latex], but so are [latex]3y = 15[/latex] and [latex]0.5 y = 2.5[/latex]. The reader is left to ponder the use of the definite article the in Equations 1.5 and 1.6. Regardless of which form the equation of a line takes, note that the variables involved are all raised to the first power.[7] For instance, there are no [latex]\sqrt{x}[/latex] terms, no [latex]y^2[/latex] terms or any variables appearing in denominators. Let's look at a few examples.
Example 1.3.3
Example 1.3.3.1a
Graph the following equations in the [latex]xy[/latex]-plane:
[latex]y = 3x - 1[/latex]
Solution:
To graph a line, we need just two points on that line. There are several ways to do this, and we showcase two of them here.
Graph [latex]y=3x-1[/latex] on the [latex]xy[/latex]-plane.
We recognize that [latex]y = 3x-1[/latex] is in slope-intercept form, [latex]y = mx+b,[/latex] with [latex]m = 3[/latex] and [latex]b = -1.[/latex] This immediately gives us one point on the graph -- the [latex]y[/latex]-intercept [latex](0,-1).[/latex]
From here, we use the slope [latex]m = 3 = \dfrac{3}{1}[/latex] and move one unit to the right and three units up, to obtain a second point on the line, [latex](1,2).[/latex] Connecting these points gives us the next graph.
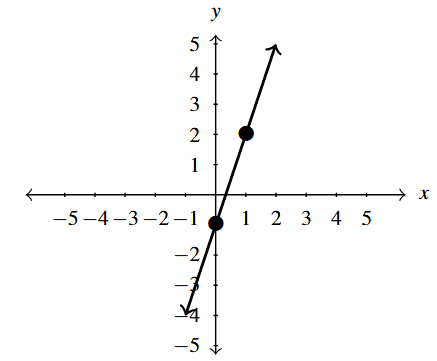
Example 1.3.3.1b
Graph the following equations in the [latex]xy[/latex]-plane:
[latex]2x + 4y = 3[/latex]
Solution:
To graph a line, we need just two points on that line. There are several ways to do this, and we showcase two of them here.
Graph [latex]2x+4y=3[/latex] on the [latex]xy[/latex]-plane.
The equation [latex]2x+4y = 3[/latex] is a general form of a line. To get two points here, we choose convenient values for one of the variables, and solve for the other variable.
Choosing [latex]x=0,[/latex] for example, reduces [latex]2x+4y = 3[/latex] to [latex]4y = 3[/latex], or [latex]y = \dfrac{3}{4}.[/latex]
This means the point [latex]\left(0, \dfrac{3}{4} \right)[/latex] is on the graph.
Choosing [latex]y = 0[/latex] gives [latex]2x = 3[/latex], or [latex]x = \dfrac{3}{2}.[/latex]
This gives is a second point on the line, [latex]\left(\dfrac{3}{2}, 0 \right)[/latex].[8] Our graph of [latex]2x+4y = 3[/latex] is next.
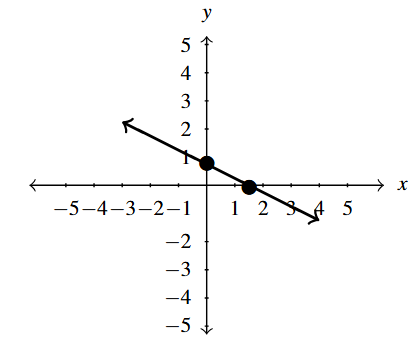
Example 1.3.3.2
Write the slope-intercept form of the line containing the points [latex](-1,3)[/latex] and [latex](2,1).[/latex]
Solution:
Write the slope-intercept form of the line containing the points [latex](-1,3)[/latex] and [latex](2,1).[/latex]
We'll assume we're using the familiar [latex](x,y)[/latex] axis labels and begin by finding the slope of the line using Equation 1.3: [latex]m = \dfrac{\Delta y}{\Delta x} = \dfrac{1 - 3}{2 - (-1)} = -\dfrac{2}{3}.[/latex]
Next, we substitute this result, along with one of the given points, into the point-slope equation of the line, Equation 1.5. We have two options for the point [latex]\left(x_{0}, y_{0}\right).[/latex] We'll use [latex](-1,3)[/latex] and leave it to the reader to check that using [latex](2,1)[/latex] results in the same equation. Substituting into the point-slope form of the line, we get
\[\begin{array}{rclr}
y - y_{0} & = & m\left(x - x_{0}\right) & \\
y - 3 & = & -\dfrac{2}{3} \left(x - (-1)\right) & \\ & & & \\
y - 3 & = & -\dfrac{2}{3} \left(x +1 \right) & \\ & & & \\
y - 3& = & -\dfrac{2}{3}x - \dfrac{2}{3}\\ & & & \\
y& = & -\dfrac{2}{3}x - \dfrac{2}{3} + 3\\ & & & \\
y & = & -\dfrac{2}{3} x + \dfrac{7}{3}. \\ & & & \\
\end{array} \]
We can check our answer by showing that both [latex](-1,3)[/latex] and [latex](2,1)[/latex] are on the graph of [latex]y = -\dfrac{2}{3} x + \dfrac{7}{3}[/latex] algebraically by showing that the equation holds true when we substitute [latex]x = -1[/latex] and [latex]y=3[/latex] and when [latex]x = 2[/latex] and [latex]y = 1.[/latex]
Example 1.3.3.3
Write the slope-intercept form of the equation of the line below:
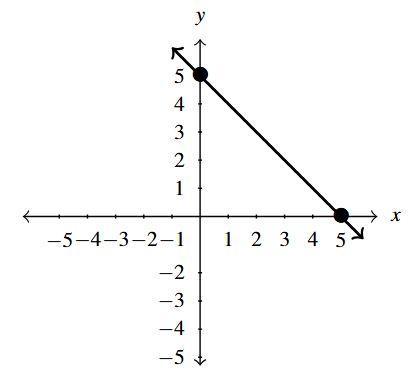
Solution:
Write the slope-intercept form of the equation of the line graphed above.
From the graph, we see that the points [latex](0,5)[/latex] and [latex](5,0)[/latex] are on the line, so we may proceed as we did in the previous problem.
We compute the slope [latex]m = \dfrac{\Delta y}{\Delta x} = \dfrac{0 - 5}{5 - 0} = -1.[/latex]
As before, we have two points to choose from to substitute into the point-slope formula, and, as before, we'll select one of them, [latex](0,5)[/latex] and leave the computations with [latex](5,0)[/latex] to the reader.
\[\begin{array}{rclr}
y - y_{0} & = & m\left(x - x_{0}\right) & \\
y - 5 & = & (-1) \left(x -0 \right) & \\
y- 5 & = &-x & \\
y& = & -x + 5.\\
\end{array} \]
As before we can check this line contains both points [latex](x,y) = (0,5)[/latex] and [latex](x,y) = (5,0)[/latex] algebraically.
While every point on a line holds value and meaning,[9] we've reminded you of certain points, called intercepts, which hold special enough significance to be singled out. Formally, we define these as follows.
Given a graph of an equation in the [latex]xy[/latex]-plane:
- A point on a graph which is also on the [latex]x[/latex]-axis is called an [latex]x[/latex]-intercept of the graph. To determine the [latex]x[/latex]-intercept(s) of a graph, set [latex]y = 0[/latex] in the equation and solve for [latex]x.[/latex]
NOTE: [latex]x[/latex]-intercepts always have the form: [latex](x_{0},0).[/latex] - A point on a graph which is also on the [latex]y[/latex]-axis is called an [latex]y[/latex]-intercept of the graph. To determine the [latex]y[/latex]-intercept(s) of a graph, set [latex]x = 0[/latex] in the equation and solve for [latex]y.[/latex]
NOTE: [latex]y[/latex]-intercepts always have the form: [latex](0,y_{0}).[/latex]
As usual, the labels of the axes in the problem will dictate the labels on the intercepts. If we're working in the [latex]vw[/latex]-plane, for instance, there would be [latex]v[/latex]- and [latex]w[/latex]-intercepts.
The last little bit of analytic geometry we need to review about lines are the concepts of parallel and perpendicular lines. Parallel lines do not intersect,[10] and hence, parallel lines necessarily have the same slope. Perpendicular lines intersect at a right ([latex]90^{\circ}[/latex]) angle. The relationship between these slopes is somewhat more complicated, and is summarized below.
Suppose line [latex]L_{1}[/latex] has slope [latex]m_{1}[/latex] and line [latex]L_{2}[/latex] has slope [latex]m_{2}:[/latex]
- [latex]L_{1}[/latex] and [latex]L_{2}[/latex] are parallel (written [latex]L_{1} \parallel L_{2}[/latex]) if and only if [latex]m_{1} = m_{2}.[/latex]
- If [latex]m_{1} \neq 0[/latex] and [latex]m_{2} \neq 0[/latex] then [latex]L_{1}[/latex] and [latex]L_{2}[/latex] are perpendicular (written [latex]L_{1} \perp L_{2}[/latex]) if and only if [latex]m_{1} m_{2} = -1.[/latex]
NOTE: [latex]m_{1} m_{2} = -1[/latex] is equivalent to [latex]m_{2} = -\dfrac{1}{m_{1}}[/latex], so that perpendicular lines have slopes which are opposite reciprocals of one another.
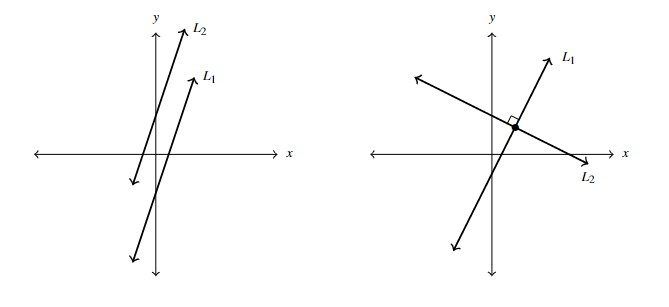
A few remarks about Theorem 1.3 are in order. First off, the theorem assumes that the slopes of the lines exist. The reader is encouraged to think about the case when one (or both) of the slopes don't exist. Along those same lines, the reader is encouraged to think about why the stipulations [latex]m_{1} \neq 0[/latex] and [latex]m_{2} \neq 0[/latex] appear in the statement regarding slopes of perpendicular lines, and what happens in this case as well. (Think geometrically!) In Exercise 41, you'll prove the assertion about the slopes of perpendicular lines. For now, we accept it as true and use it in the following example.
Example 1.3.4
Example 1.3.4.1
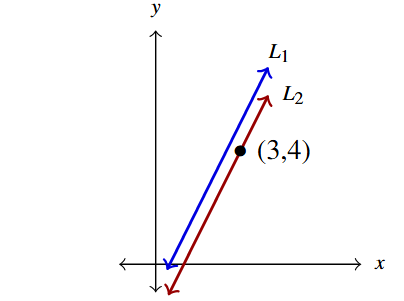
For line [latex]y = 2x-1[/latex] and the point [latex](3,4),[/latex] write the equation of the line parallel to the given line which contains the given point. Check your answers by graphing them, along with the original line.
Solution:
For line [latex]y = 2x-1[/latex] and the point [latex](3,4),[/latex] write the equation of the line parallel to the given line which contains the given point. Check your answers by graphing them, along with the original line.
Seeing as [latex]y = 2x-1[/latex] is already in slope-intercept form, we have the slope [latex]m = 2.[/latex] To find the line parallel to this line containing [latex](3,4),[/latex] we use the point-slope form with [latex]m = 2[/latex] to get:
\[\begin{array}{rclr}
y - y_{0} & = & m\left(x - x_{0}\right) & \\
y - 4 & = & 2 \left(x - 3\right) & \\
y - 4 & = & 2x - 6 & \\
y& = & 2x-2\\
\end{array} \]
Algebraically, we can verify that the slope is indeed 2 and that when [latex]x =3[/latex] we get [latex]y = 4.[/latex] Using a graph centered at the point [latex](3, 4),[/latex] we graph both [latex]y = 2x-1[/latex] (in blue) and [latex]y = 2x-2[/latex] (in red) and observe that they appear to be parallel.
Example 1.3.4.2
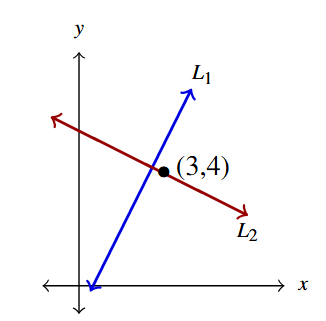
For line [latex]y = 2x-1[/latex] and the point [latex](3,4),[/latex] write the equation of the line perpendicular to the given line which contains the given point. Check your answers by graphing them, along with the original line.
Solution:
For line [latex]y = 2x-1[/latex] and the point [latex](3,4),[/latex] write the equation of the line perpendicular to the given line which contains the given point. Check your answers by graphing them, along with the original line.
To find the line perpendicular to [latex]y = 2x-1[/latex] containing [latex](3,4),[/latex] we use the slope [latex]m = -\dfrac{1}{2}[/latex] in the point-slope formula:
\[\begin{array}{rclr}
y - y_{0} & = & m\left(x - x_{0}\right) & \\ & & & \\
y - 4 & = & -\dfrac{1}{2} \left(x - 3\right) & \\ & & & \\
y - 4 & = & -\dfrac{1}{2} x + \dfrac{3}{2} & \\ & & & \\
y& = & -\dfrac{1}{2} x + \dfrac{11}{2}\\
\end{array} \]
Algebraically, we check that the slope is [latex]m = -\dfrac{1}{2}[/latex] and when [latex]x = 3[/latex] we get [latex]y = 4[/latex] as required. When checking using a graph of [latex]y=2x-1[/latex] (in blue) and [latex]y = -\dfrac{1}{2}x + \dfrac{11}{2}[/latex] (in red), we center the picture at [latex](3, 4)[/latex] and had to square up the graph, to truly observe the perpendicular nature of the lines.
Our next example with lines sets up a fourth kind of symmetry which will be revisited in Section 5.1.
Example 1.3.5
Example 1.3.5
Show that the points [latex](a,b)[/latex] and [latex](b,a)[/latex] in the [latex]xy[/latex]-plane are symmetric about the line [latex]y = x.[/latex]
Solution:
If [latex]a = b[/latex] then [latex](a, b) = (a, a) = (b, a)[/latex] and this point lies on the line [latex]y = x.[/latex][11] To prove the claim for the case when [latex]a \neq b,[/latex] we will show that the line [latex]y = x[/latex] is a perpendicular bisector of the line segment with endpoints [latex](a,b)[/latex] and [latex](b,a),[/latex] as illustrated below.
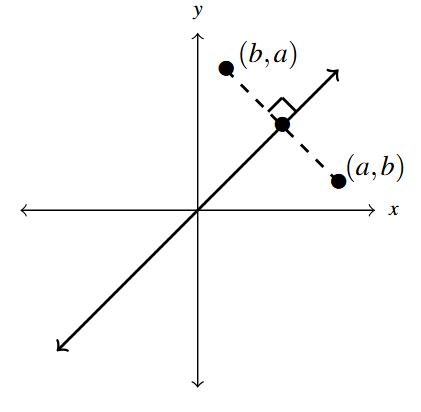
To show the perpendicular part, we first note the slope of the line containing [latex](a,b)[/latex] and [latex](b,a)[/latex] is
\[ m= \dfrac{a-b}{b-a} = \dfrac{\cancel{(a-b)}}{-\cancel{(a-b)}} = -1\]
Due to the fact that the slope of [latex]y = x = 1x + 0[/latex] is [latex]m = 1,[/latex] we see that the slopes of these two lines are negative reciprocals. Hence, [latex]y=x[/latex] and the line segment with endpoints [latex](a,b)[/latex] and [latex](b,a)[/latex] are perpendicular. For the bisector part, we use Equation 1.2 to compute the midpoint of the line segment with endpoints [latex](a,b)[/latex] and [latex](b,a):[/latex]
\[ \begin{array}{rcl}
M & = & \left( \dfrac{a+b}{2}, \dfrac{b+a}{2} \right) \\[10pt]
& = & \left( \dfrac{a+b}{2}, \dfrac{a+b}{2} \right) \\ \end{array} \]
As the [latex]x[/latex] and [latex]y[/latex] coordinates of this point are the same, we determine that the midpoint lies on the line [latex]y=x.[/latex]
1.3.2 Constant Functions
Now that we have defined the concept of a function, we'll spend the rest of Chapter 1 revisiting families of curves from prior courses in Algebra by viewing them through a function lens. We start with lines and refer the reader to the previous subsection for a review of the basic properties of lines. The simplest lines are vertical and horizontal lines. We leave it to the reader (see Exercise 94) to think about why we eschew vertical lines in our discussion here, and begin with a functional description of horizontal lines.
Consider the horizontal lines graphed in the [latex]xy[/latex]-plane as shown below. The Vertical Line Test, Theorem 1.2, tells us that each describes [latex]y[/latex] as a function of [latex]x[/latex] so the question becomes how to represent these functions algebraically. The key here is to remember that the equation relating the independent variable [latex]x,[/latex] the dependent variable [latex]y,[/latex] and the function [latex]f[/latex] is given by [latex]y = f(x).[/latex]

In the graph on the left, [latex]y[/latex] always equals 3 so we have [latex]f(x) = 3.[/latex] Procedurally, [latex]f(x) = 3[/latex] says that the rule [latex]f[/latex] takes the input [latex]x,[/latex] and, regardless of that input, gives the output 3. This is an example of what is called a constant function - a function which returns the same value regardless of the input. Likewise, the function represented by the graph in the middle is [latex]f(x) = -2,[/latex] and the graph on the right (the [latex]x[/latex]-axis) is the graph of [latex]f(x) = 0.[/latex] In general, we have the following definition:
A constant function is a function of the form \[ f(x) = b\] where [latex]b[/latex] is real number. The domain of a constant function is [latex](-\infty, \infty).[/latex]
Some remarks about Definition 1.9 are in order. First, note that we are using [latex]x[/latex] as the independent variable, [latex]f[/latex] as the function name, and the letter [latex]b[/latex] as a parameter. In this context, a parameter is a fixed, but arbitrary, constant used to describe a family of functions. Different values of [latex]b[/latex] determine different constant functions. For example, [latex]b = 3[/latex] gives [latex]f(x) = 3[/latex], [latex]b = -2[/latex] gives [latex]f(x) = -2,[/latex] and so on. Once [latex]b[/latex] is chosen, however, it does not change as the independent variable, [latex]x,[/latex] changes.
Also note that we are using the generic defaults for function names and independent variables, namely [latex]f[/latex] and [latex]x[/latex], respectively. The functions [latex]G(t) = \sqrt{\pi}[/latex] and [latex]Z(\rho) = 0[/latex] are also fine examples of constant functions. Recall that inherent in the definition of a function is the notion of domain, so we record (as part of the definition) that a constant function has domain [latex](-\infty, \infty)[/latex]. The range of a constant function is the set [latex]\{b \}[/latex]. The value [latex]b[/latex] in this case is both the maximum and minimum of [latex]f[/latex], attained at each value in its domain.[12]
The next example showcases an application of constant functions and introduces the notion of a piecewise-defined function.
Example 1.3.6
Example 1.3.6.1
The price of admission to see a matinee showing at a local movie theater is a function of the age of the ticket holder. If a person is aged [latex]A[/latex] years, the price per ticket is [latex]p(A)[/latex] dollars and is given by:
\[ p(A) = \begin{array}{rc}
5.75 & \text{if } 0 \leq A < 6 \\
7.25 & \text{if } 6 \leq A < 50 \\
5.75 & \text{if }A \geq 50 \\
\end{array}
\]
Compute and interpret [latex]p(3)[/latex], [latex]p(6)[/latex] and [latex]p(62).[/latex]
Solution:
The function [latex]p(A)[/latex] described above is an example of a piecewise-defined function because the rule to determine outputs, not just the value of the output, changes depending on the inputs.
Compute and interpret [latex]p(3)[/latex], [latex]p(6)[/latex] and [latex]p(62)[/latex].
To find [latex]p(3)[/latex], we note that the value [latex]A = 3[/latex] satisfies the inequality [latex]0 \leq A[/latex] < 6 so we use the rule [latex]p(A) = 5.75.[/latex] Hence, [latex]p(3) = 5.75[/latex] which means a ticket for a 3 year old is $5.75.
The next age, [latex]A = 6[/latex], just barely satisfies the inequality [latex]6 \leq A[/latex] < 50 so we use the rule [latex]p(A) = 7.25,[/latex] This yields [latex]p(6) = 7.25[/latex] which means a ticket for a 6 year old is $7.25.
Lastly, [latex]A = 62[/latex] satisfies the inequality [latex]A \geq 50,[/latex] so we are back to the rule [latex]p(A) = 5.75.[/latex] Thus [latex]p(62) = 5.75[/latex] which means someone 62 years young gets in for $5.75.
Example 1.3.6.2
The price of admission to see a matinee showing at a local movie theater is a function of the age of the ticket holder. If a person is aged [latex]A[/latex] years, the price per ticket is [latex]p(A)[/latex] dollars and is given by:
\[ p(A) = \begin{array}{rc}
5.75 & \text{if } 0 \leq A < 6 \\
7.25 & \text{if } 6 \leq A < 50 \\
5.75 & \text{if }A \geq 50 \\
\end{array}
\]
Explain the pricing structure verbally.
Solution:
The function [latex]p(A)[/latex] described above is an example of a piecewise-defined function because the rule to determine outputs, not just the value of the output, changes depending on the inputs.
Explain the pricing structure verbally.
Now that we've had some practice interpreting function values, we can begin to verbalize what the function is really saying. In the first piece of the function, the inequality [latex]0 \leq A[/latex] < 6 describes ticket holders under the age of 6 years and the inequality [latex]A \geq 50[/latex] describes ticket holders fifty years old or or older.
For folks in these two age demographics, [latex]p(A) = 5.75[/latex] so the price per ticket is $5.75 For everyone else, that is for folks at least 6 but younger than 50, the price is $7.25 per ticket.
Example 1.3.6.3
The price of admission to see a matinee showing at a local movie theater is a function of the age of the ticket holder. If a person is aged [latex]A[/latex] years, the price per ticket is [latex]p(A)[/latex] dollars and is given by:
\[ p(A) = \begin{array}{rc}
5.75 & \text{if } 0 \leq A < 6 \\
7.25 & \text{if } 6 \leq A < 50 \\
5.75 & \text{if }A \geq 50 \\
\end{array}
\]
Graph [latex]p(A).[/latex]
Solution:
The function [latex]p(A)[/latex] described above is an example of a piecewise-defined function because the rule to determine outputs, not just the value of the output, changes depending on the inputs.
Graph [latex]p(A).[/latex]
The independent variable here is specified as [latex]A[/latex], so we'll label our horizontal axis that way. The dependent variable remains unspecified so we can use the default [latex]y.[/latex]
The graph of [latex]y = p(A)[/latex] consists of three horizontal line pieces: the first is [latex]y = 5.75[/latex] for [latex]0 \leq A[/latex] < 6, the second piece is [latex]y = 7.25[/latex] for [latex]6 \leq A[/latex] < 50, and the last piece is [latex]y = 5.75[/latex] for [latex]A \geq 50.[/latex]
For the first piece, note that [latex]A = 0[/latex] is included in the inequality [latex]0 \leq A[/latex] < 6 but [latex]A = 6[/latex] is not. For this reason, we have a point indicated at [latex](0, 5.75)[/latex] but leave a hole[13] at [latex](6, 5.75).[/latex]
Similarly, to graph the second piece, we begin with a point at [latex](6, 7.25)[/latex] and continue the horizontal line to a hole at [latex](50, 7.25).[/latex]
Lastly, we finish the graph with a point at [latex](50, 5.75)[/latex] and continue to the right indefinitely.[14] Note the scaling on the horizontal axis compared to the vertical axis.
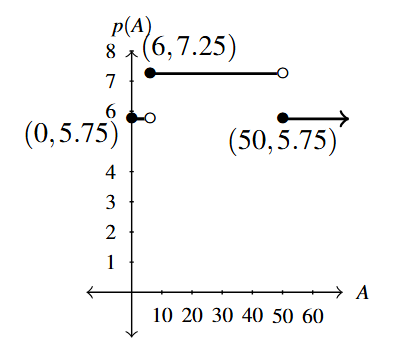
One of the favorite piecewise-defined functions in mathematical circles is the greatest integer of [latex]x[/latex], denoted by [latex]\lfloor x \rfloor[/latex]. In Section 0.1.1 we defined the set of integers as [latex]\mathbb{Z} = \{ \ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}[/latex].[15] The value [latex]\lfloor x \rfloor[/latex] is defined to be the largest integer [latex]k[/latex] with [latex]k \leq x.[/latex] That is, [latex]\lfloor x \rfloor[/latex] is the unique integer [latex]k[/latex] such that [latex]k \leq x[/latex] < [latex]k+1.[/latex] Said differently, given any real number [latex]x,[/latex] if [latex]x[/latex] is an integer, then [latex]\lfloor x \rfloor = x.[/latex] If not, then [latex]x[/latex] lies in an interval between two integers, [latex]k[/latex] and [latex]k+1[/latex] and we choose [latex]\lfloor x \rfloor = k,[/latex] the left endpoint.
Example 1.3.7
Example 1.3.7a
Let [latex]\lfloor x \rfloor[/latex] denote the greatest integer function. Compute [latex]\lfloor 0.785 \rfloor[/latex], [latex]\lfloor 117 \rfloor[/latex], [latex]\lfloor -2.001 \rfloor[/latex] and [latex]\lfloor \pi + 6 \rfloor.[/latex]
Solution:
Compute [latex]\lfloor 0.785 \rfloor, \; \lfloor 117 \rfloor, \; \lfloor -2.001 \rfloor[/latex] and [latex]\lfloor \pi + 6 \rfloor.[/latex]
To find [latex]\lfloor 0.785 \rfloor,[/latex] we note that [latex]0 \leq 0.785[/latex] < 1 so [latex]\lfloor 0.785 \rfloor = 0.[/latex]
Given that 117 is an integer, we have [latex]\lfloor 117 \rfloor = 117.[/latex]
To find [latex]\lfloor -2.001 \rfloor,[/latex] we note that [latex]-3 \leq -2.001[/latex] < [latex]-2,[/latex] so [latex]\lfloor -2.001 \rfloor = -3.[/latex]
Finally, with [latex]\pi \approx 3.14,[/latex] we get [latex]\pi + 6 \approx 9.14[/latex] and [latex]9 \leq \pi+6[/latex] < 10 so [latex]\lfloor \pi + 6 \rfloor = 9.[/latex]
Example 1.3.7b
Let [latex]\lfloor x \rfloor[/latex] denote the greatest integer function. Explain how we can view [latex]\lfloor x \rfloor[/latex] as a piecewise-defined function and use this to graph [latex]y = \lfloor x \rfloor.[/latex]
Solution:
Explain how we can view [latex]\lfloor x \rfloor[/latex] as a piecewise-defined function and use this to graph [latex]y = \lfloor x \rfloor.[/latex]
The first step in evaluating [latex]\lfloor x \rfloor[/latex] is to determine the interval [latex][k, k+1)[/latex] containing [latex]x[/latex] so it seems reasonable that these are the intervals which produce the pieces. In this case, there happen to be infinitely many pieces. The inequality [latex]k \leq x[/latex] < [latex]k+1[/latex] includes the left endpoint but excludes the right endpoint, so we have points at the left endpoints of our horizontal line segments while we have holes at the right endpoints.
A partial description of [latex]\lfloor x \rfloor[/latex] is given alongside a partial graph. (A full description or a complete graph would require infinitely large paper!) We use the vertical dots [latex]\, \smash{\vdots} \,[/latex] to indicate that both the rule and the graph continue indefinitely following the established pattern.
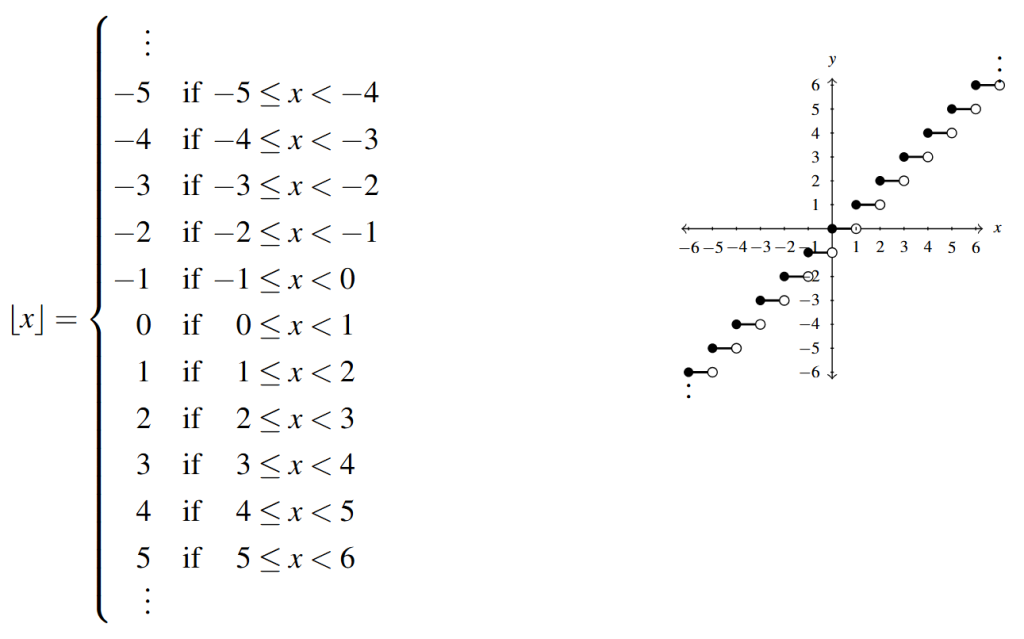
1.3.3 Linear Functions
Now that we've discussed the functions which correspond to horizontal lines, [latex]y = b,[/latex] we move to discussing the functions which can be represented by lines of the form [latex]y = mx + b[/latex] where [latex]m \neq 0.[/latex] These functions are called linear functions and are described below.
A linear function is a function of the form \[ f(x) = mx + b,\] where [latex]m[/latex] and [latex]b[/latex] are real numbers with [latex]m \neq 0.[/latex] The domain of a linear function is [latex](-\infty, \infty).[/latex]
As with Definition 1.9, in Definition 1.10, [latex]x[/latex] is the
independent variable, [latex]f[/latex] is the function name, and both [latex]m[/latex] and [latex]b[/latex] are parameters. Notice that [latex]m[/latex] is restricted by [latex]m \neq 0[/latex] for if [latex]m = 0[/latex] then the function [latex]f(x) = mx + b[/latex] would reduce to the constant function [latex]f(x) = b[/latex]. The domain of linear functions, like that of constant functions, is specified as [latex](-\infty, \infty)[/latex].
Recall that the form of the line [latex]y = mx + b[/latex] is called the slope-intercept form of the line and the slope, [latex]m[/latex], and the [latex]y[/latex]-intercept [latex](0, b)[/latex], are easily determined when the line is written this way. Likewise, the form of the function in Definition 1.10, [latex]f(x) = mx + b[/latex], is often called the slope-intercept form of a linear function.
The graph of a linear function is the graph of the line [latex]y = mx + b[/latex]. Lines are uniquely determined by two points, and two points of geometric interest are the axis intercepts. We've already reminded you of the [latex]y[/latex]-intercept, [latex](0,b)[/latex], which is obtained by setting [latex]x = 0[/latex]. Similarly, to find the [latex]x[/latex]-intercept, we set [latex]y = 0[/latex] and solve [latex]mx + b = 0[/latex] for [latex]x[/latex]. We leave this to the reader in Exercise 79. In addition to having special graphical significance, axis intercepts quite often play important roles in applications involving both linear and non-linear functions. For that reason, we take the time to remind you of the definitions of intercepts (1.8) here using function notation.
Suppose [latex]f[/latex] is a function represented by the graph of [latex]y = f(x).[/latex]
- If 0 is in the domain of [latex]f[/latex] then the point [latex](0, f(0))[/latex] is the [latex]y[/latex]-intercept of the graph of [latex]y = f(x).[/latex]
That is, [latex](0,f(0))[/latex] is where the graph meets the [latex]y[/latex]-axis. - If 0 is in the range of [latex]f[/latex] then the solutions to [latex]f(x) = 0[/latex] are called the zeros of [latex]f.[/latex] If [latex]c[/latex] is a zero of [latex]f[/latex] then the point [latex](c,0)[/latex] is an [latex]x[/latex]-intercept of the graph of [latex]y = f(x).[/latex]
That is, [latex](c,0)[/latex] is where the graph meets the [latex]x[/latex]-axis.
As is customary in this text, the above definition uses the default independent variable [latex]x[/latex], function name [latex]f[/latex], and dependent variable [latex]y[/latex], so these letters will change depending on the context. Also note that the zeros of a function are the solutions to [latex]f(x) = 0[/latex] - so they are real numbers. The [latex]x[/latex]-intercepts are, on the other hand, points on the graph. As a quick example, consider [latex]f(x) = x-3[/latex]. The zeros of [latex]f[/latex] are found by solving [latex]f(x) = 0[/latex], or [latex]x-3=0[/latex]. We get one solution, [latex]x = 3[/latex]. Therefore, [latex]x=3[/latex] is the zero of [latex]f[/latex] that corresponds graphically to the [latex]x[/latex]-intercept [latex](3,0)[/latex].
We now turn our attention to slope. The role of slope, or more generally a rate of change, in Science and Mathematics cannot be overstated.[16] As you may recall, the slope of a line that has been graphed in the [latex]xy[/latex]-plane is defined geometrically as follows:
\[m = \dfrac{\text{rise}}{\text{run}} = \dfrac{\Delta y}{\Delta x} ,\]
where the capital Greek letter [latex]\Delta[/latex] denotes change in.[17] In this course, it is vital that we regard the slope of a linear function as a rate of change of function outputs to function inputs. That is, given the graph of a linear function [latex]y = f(x) = mx + b[/latex]:
\[ m = \dfrac{\text{rise}}{\text{run}} = \dfrac{\Delta y}{\Delta x} = \dfrac{\Delta [f(x)]}{\Delta x} = \dfrac{\Delta \text{outputs}}{\Delta \text{inputs}}. \]
What is important to note here is that for linear functions, the rate of change [latex]m[/latex] is constant for all values in the domain. We'll see the importance of this statement in the upcoming examples.
Geometrically, the sign of the slope has a profound impact on the graph of the line. Recall that if the slope [latex]m > 0[/latex], the line rises as we read from left to right; if [latex]m[/latex] < 0, the line falls as we read from left to right; if [latex]m=0[/latex], we have a horizontal line and the graph plateaus.
Example 1.3.8
Example 1.3.8.1
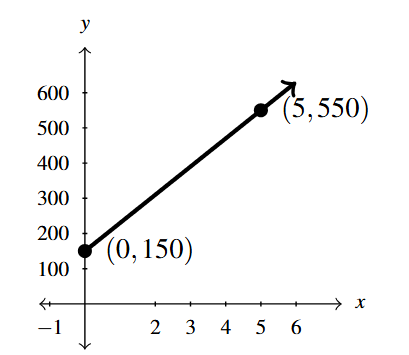
The cost, in dollars, to produce [latex]x[/latex] PortaBoy game systems for a local retailer is given by [latex]C(x) = 80x + 150[/latex] for [latex]x \geq 0.[/latex] Compute and interpret [latex]C(0)[/latex] and [latex]C(5)[/latex] and use these to graph [latex]y = C(x).[/latex]
Solution:
Compute and interpret [latex]C(0)[/latex] and [latex]C(5)[/latex] and use these to graph [latex]y = C(x).[/latex]
To find [latex]C(0)[/latex], we substitute 0 for [latex]x[/latex] in the formula [latex]C(x)[/latex] and obtain: [latex]C(0) = 80(0) + 150 = 150[/latex]. Given that [latex]x[latex] represents the number of PortaBoys produced and [latex]C(x)[/latex] represents the cost to produce said PortaBoys, [latex]C(0) = 150[/latex] means it costs $150 even if we don't produce any PortaBoys at all. At first, this may not seem realistic, but that $150 is often called the fixed or start-up cost of the venture. Things like re-tooling equipment, leasing space, or any other up front costs get lumped into the fixed cost.
To find [latex]C(5)[/latex], we substitute 5 for [latex]x[/latex] in the formula [latex]C(x)[/latex]: [latex]C(5) = 80(5)+150 = 550[/latex]. This means it costs $550 to produce 5 PortaBoys for the local retailer.
These two computations give us two points on the graph: [latex](0, C(0))[/latex] and [latex](5, C(5)).[/latex] Along with the domain restriction [latex]x \geq 0,[/latex] we get:
Example 1.3.8.2
The cost, in dollars, to produce [latex]x[/latex] PortaBoy game systems for a local retailer is given by [latex]C(x) = 80x + 150[/latex] for [latex]x \geq 0.[/latex] Explain the significance of the restriction on the domain, [latex]x \geq 0.[/latex]
Solution:
Explain the significance of the restriction on the domain, [latex]x \geq 0.[/latex]
In this context, [latex]x[/latex] represents the number of PortaBoys produced. It makes no sense to produce a negative quantity of game systems,[18] so [latex]x \geq 0[/latex].
Example 1.3.8.3
The cost, in dollars, to produce [latex]x[/latex] PortaBoy game systems for a local retailer is given by [latex]C(x) = 80x + 150[/latex] for [latex]x \geq 0.[/latex] Interpret the slope of [latex]y = C(x)[/latex] geometrically and as a rate of change.
Solution:
Interpret the slope of [latex]y = C(x)[/latex] geometrically and as a rate of change.
The cost function [latex]C(x)= 80x + 150[/latex] is in slope-intercept form so we recognize the slope as the coefficient of [latex]x[/latex], [latex]m = 80[/latex]. With [latex]m > 0[/latex], the function [latex]C[/latex] is always increasing. This means that it costs more money to make more game systems. To interpret the slope as a rate of change, we note that the output, [latex]C(x)[/latex], is the cost in dollars, while the input, [latex]x[/latex], is the number of PortaBoys produced:
\[ \begin{array}{rcl} m &=& 80 \\ &=& \dfrac{80}{1} \\ & & \\ &=& \dfrac{\Delta [C(x)]}{\Delta x} \\ & & \\ &=& \dfrac{80 \text{ dollars}}{1 \, \text{PortaBoy produced}}. \end{array}\]
Hence, the cost to produce PortaBoys is increasing at a rate of $80 per PortaBoy produced. This is often called the variable cost for the venture.
Example 1.3.8.4
The cost, in dollars, to produce [latex]x[/latex] PortaBoy game systems for a local retailer is given by [latex]C(x) = 80x + 150[/latex] for [latex]x \geq 0.[/latex] How many PortaBoys can be produced for $15,000?
Solution:
How many PortaBoys can be produced for $15,000?
To find how many PortaBoys can be produced for $15,000, we solve [latex]C(x) = 15000,[/latex] which means [latex]80x+150 = 15000.[/latex] This yields [latex]x = 185.625.[/latex] We can produce only a whole number amount of PortaBoys so we are left with two options: produce 185 or 186 PortaBoys. Given that [latex]C(185) = 14950[/latex] and [latex]C(186) = 15030.[/latex] We would be over budget if we produced 186 PortaBoys, hence, we can produce 185 PortaBoys for $15,000 (with $50 to spare).
A couple of remarks about Example 1.3.8 are in order. First, if [latex]x[/latex] represents the number of PortaBoy game systems being produced, then [latex]x[/latex] can really only take on whole number values. We will revisit this scenario in Section 2.1 where we will see how the approach presented here allows us to use more elegant techniques when analyzing the situation than a discrete data set would allow.[[19]
Second, once we know that the variable cost is $80 per PortaBoy, we can revisit a computation we did earlier in the example. We computed [latex]C(185) = 14950[/latex] and needed to compute [latex]C(186)[/latex]. With [latex]186[/latex] being just one more PortaBoy than [latex]185[/latex], we can use the variable cost to get \[ \begin{array}{rcl} C(186) &=& C(185) + 80(1) \\ &=& 14950 + 80 \\ &=& 15030, \\ \end{array} \] which agrees with our earlier computation.[20] If we wanted to find [latex]C(300)[/latex], we could do something similar. Using [latex]300 - 185 = 115[/latex], we can find [latex]C(300)[/latex] as follows: \[ \begin{array}{rcl} C(300) &=& C(185) + 80(115) \\ &=& 14950 + 9200 \\ &=& 24150. \\\end{array}\] In general, we could rewrite [latex]C(x) = C(185) + 80(x - 185)[/latex]. This same reasoning shows that for any [latex]x_{0}[/latex] in the domain of [latex]C[/latex], we have [latex]C(x) = C(x_{0}) + 80(x - x_{0})[/latex] - a fact we invite the reader to verify.[21]
Indeed, the computations above are at the heart of what it means to be a linear function: linear functions change at a constant rate known as the slope. To better see this algebraically, recall that given a point [latex](x_{0}, y_{0})[/latex] on a line along with the slope, [latex]m[/latex], the point-slope form of the line is: [latex]y - y_{0} = m(x - x_{0})[/latex]. Rewriting, we get [latex]y = y_{0} + m (x - x_{0})[/latex] and setting [latex]y = f(x)[/latex] and [latex]y_{0} = f(x_{0})[/latex] yields:
A few remarks are in order. First note that if the point [latex](x_{0}, f(x_{0}))[/latex] is the [latex]y[/latex]-intercept [latex](0, b),[/latex] Equation 1.8 immediately reduces to the slope-intercept form of the line: \[ \begin{array}{rcl} f(x) &=& f(x_{0}) + m (x - x_{0}) \\ &=& b + m(x - 0) \\ &=& mx + b,\\ \end{array} \] so you can use Equation 1.8 exclusively from this point forward.[22]
Second, if we write [latex]\Delta x = x - x_{0},[/latex] then [latex]x = x_{0} + \Delta x[/latex] so we can rewrite Equation 1.8 as follows:
\[ \begin{array}{ccccc}
f(x_{0} + \Delta x) & = & f(x_{0}) & + & m \Delta x \\
(\text{new output}) & = & (\text{known output}) & +& (\text{change in outputs}) \\ \end{array} \]
In other words, changing the input by [latex]\Delta x[/latex] results in changing the output by [latex]m \Delta x.[/latex] This tracks because \[ m \Delta x = \dfrac{\Delta [f(x)]}{\Delta x} \Delta x = \Delta[f(x)] = \Delta \text{outputs}. \]
The fact that we can write [latex]\Delta \text{outputs} = m \Delta x[/latex] for any choice of [latex]x_{0}[/latex] is another way to see that for linear functions, the rate of change is constant. That is, the rate of change, [latex]m[/latex], is the same for all values [latex]x_{0}[/latex] in the domain. We'll put Equation 1.8 to good use in the next example.
Example 1.3.9
Example 1.3.9.1
The local retailer in Example 1.3.8 is trying to mathematically model the relationship between the number of PortaBoy systems sold and the price per system. Suppose 20 systems were sold when the price was $220 per system, but when the systems went on sale for $190 each, sales doubled.
Find a formula for a linear function [latex]p[/latex] which represents the price [latex]p(x)[/latex] as a function of the number of systems sold, [latex]x[/latex]. Graph [latex]y = p(x)[/latex], find and interpret the intercepts, and determine a reasonable domain for [latex]p[/latex].
Solution:
Find a formula for a linear function [latex]p[/latex] which represents the price [latex]p(x)[/latex] as a function of the number of systems sold, [latex]x[/latex]. Graph [latex]y = p(x)[/latex], find and interpret the intercepts, and determine a reasonable domain for [latex]p[/latex].
We are asked to find a linear function [latex]p(x)[/latex] ostensibly because the retailer has only two data points and two points are all that is needed to determine a unique line. We know that 20 PortaBoys were sold when the price was $220 and double that, so 40 units, were sold when the price was $190. Using the language of function notation, these statements translate to [latex]p(20)=220[/latex] and [latex]p(40)=190[/latex], respectively. We first find the slope
\[ \begin{array}{rcl} m &=& \dfrac{\Delta [p(x)]}{\Delta x} \\[10pt] &=& \dfrac{190 - 220}{40 - 20} \\[10pt] &=& \dfrac{-30}{20} = -1.5 \\ \end{array} \]
and then substitute it and a pair [latex](x_{0}, p(x_{0}))[/latex] into the point-slope formula. We have two choices: [latex]x_{0} = 20[/latex] and [latex]p(x_{0}) = 220[/latex] or [latex]x_{0} = 40[/latex] and [latex]p(x_{0}) = 190[/latex]. We'll choose the former and invite the reader to use the latter - both will result in the same simplified expression. The point-slope formula yields
\[ \begin{array}{rcl} p(x) &=& p(x_{0}) + m (x - x_{0}) \\ &=& 220 + (-1.5)(x - 40) \\ \end{array} \]
which simplifies to [latex]p(x) = -1.5x + 250[/latex]. (To check this algebraically, we can verify that [latex]p(20) = 220[/latex] and [latex]p(40) = 190[/latex].)
To find the [latex]y[/latex]-intercept of the graph, we substitute [latex]x = 0[/latex] and find [latex]p(0) = 250[/latex]. Hence our [latex]y[/latex]-intercept is [latex](0, 250).[/latex]
To find the [latex]x[/latex]-intercept, we set [latex]p(x) = 0[/latex]. Solving [latex]-1.5x + 250 = 0[/latex] gives [latex]x = \dfrac{500}{3} = 166.\overline{6}[/latex], so our [latex]x[/latex]-intercept is [latex](166.\overline{6}, 0)[/latex].[23] The graph on the left is that of the line [latex]y = -1.5x + 250[/latex].

To determine a reasonable domain for [latex]p[/latex], we certainly require [latex]x \geq 0[/latex], because we can't sell a negative number of game systems.[24] Next, we require [latex]p(x) \geq 0[/latex], otherwise we'd be paying customers to buy PortaBoys.Solving [latex]-1.5 x + 250 \geq 0[/latex] results in [latex]x \leq 166.\overline{6}[/latex]. This shouldn't be too surprising as our graph passes through the [latex]x[/latex]-axis at [latex](166.\overline{6}, 0)[/latex], going from positive [latex]y[/latex]-values (hence, positive [latex]p(x)[/latex] values) to negative [latex]y[/latex] (hence negative [latex]p(x)[/latex] values).[25]Given that [latex]x[/latex] represents the number of PortaBoys sold, we need to choose to end the domain at either [latex]x = 166[/latex] or [latex]x = 167[/latex]. We have that [latex]p(166) = 1 > 0[/latex] but [latex]p(167) = -0.5[/latex] < 0 so we settle on the domain [latex][0,166][/latex].Our final answer is [latex]p(x) = -1.5x + 250[/latex] restricted to [latex]0 \leq x \leq 166[/latex] which is graphed above on the right.
Example 1.3.9.2
The local retailer in Example 1.3.8 is trying to mathematically model the relationship between the number of PortaBoy systems sold and the price per system. Suppose 20 systems were sold when the price was $220 per system, but when the systems went on sale for $190 each, sales doubled.
Interpret the slope of [latex]p(x)[/latex] in terms of price and game system sales.
Solution:
Interpret the slope of [latex]p(x)[/latex] in terms of price and game system sales.
The slope [latex]m = -1.5[/latex] represents the rate of change of the price of a system with respect to sales of PortaBoys. The slope is negative so we have that the price is decreasing at a rate of $1.50 per PortaBoy sold. (Said differently, you can sell one more PortaBoy for every $1.50 drop in price.)
Example 1.3.9.3
The local retailer in Example 1.3.8 is trying to mathematically model the relationship between the number of PortaBoy systems sold and the price per system. Suppose 20 systems were sold when the price was $220 per system, but when the systems went on sale for $190 each, sales doubled.
If the retailer wants to sell 150 PortaBoys next week, what should the price be?
Solution:
If the retailer wants to sell 150 PortaBoys next week, what should the price be?
To determine the price which will move 150 PortaBoys, we compute \[ \begin{array}{rcl} p(150) &=& -1.5(150) + 250 \\ &=& 25. \\ \end{array} \] That is, the price would have to be $25 per system.
Example 1.3.9.4
The local retailer in Example 1.3.8 is trying to mathematically model the relationship between the number of PortaBoy systems sold and the price per system. Suppose 20 systems were sold when the price was $220 per system, but when the systems went on sale for $190 each, sales doubled.
How many systems would sell if the price per system were set at $150?
Solution:
How many systems would sell if the price per system were set at $150?
If the price of a PortaBoy were set at $150, we'd have [latex]p(x) = 150[/latex], or [latex]-1.5x + 250 = 150.[/latex] This yields [latex]-1.5x = -100[/latex] or [latex]x = 66.\overline{6}.[/latex]
Again our algebraic solution lies between two whole numbers, so we find [latex]p(66) = 151[/latex] and [latex]p(67) = 149.5.[/latex]
If the price were set at $150, we'd sell 66 systems, because to sell 67 systems, we'd have to drop the price just under $150.
The function [latex]p[/latex] in Example 1.3.9 is called the price-demand function (or, sometimes called more simply a demand function) because it returns the price [latex]p(x)[/latex] associated with a certain demand [latex]x[/latex] - that is, how many products will sell.[26] These functions, along with cost functions like the one in Example 1.3.8, will be revisited in Example 2.1.3.
Our next two examples focus on writing formulas for piecewise-defined functions, the second of which models a real-world situation.
Example 1.3.10
Example 1.3.10
Determine a formula for the function [latex]L[/latex] graphed below.
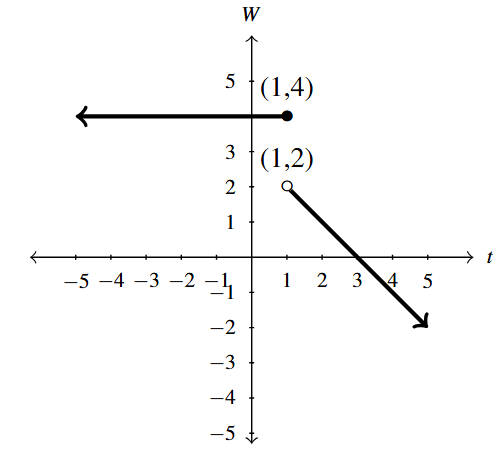
Solution:
From the graph of [latex]W = L(t)[/latex] we see that there are two distinct pieces.
Taking note of the point at [latex](1, 4)[/latex], we get [latex]L(t) = 4[/latex] for [latex]t \leq 1[/latex]. To represent [latex]L[/latex] for [latex]t>1[/latex], we use the point-slope form of a linear function:
\[L(t) = L(t_{0}) + m(t - t_{0}).\]
The only point labeled with this part of the graph is the hole at [latex](1, 2)[/latex] and it isn't technically part of the graph, so we will avoid using it.[27] Instead, we infer from the graph two other points: [latex](2, 1)[/latex] and [latex](3, 0)[/latex]. We get the slope to be
\[ \begin{array}{rcl} m &=& \dfrac{\Delta W}{\Delta t} \\ & & \\ &=& \dfrac{\Delta [L(t)]}{\Delta t} \\ & & \\ &=& \dfrac{3 - 2}{0 - 1}
\\ & & \\ &=& -1. \end{array} \]
Next, we choose a point to plug into [latex]L(t) = L(t_{0}) + m(t - t_{0})[/latex]. We have two options: [latex]t_{0} = 2[/latex] and [latex]L(t_{0}) = 1[/latex] or [latex]t_{0} = 3[/latex] and [latex]L(t_{0}) = 0[/latex]. Using the latter, we get [latex]L(t) = 0 + (-1)(t - 3)[/latex], or [latex]L(t) = -t + 3[/latex]. Putting this together with the first part, we get:
\[ L(t) = \left\{ \begin{array}{rc}
4 & \text{if } t \leq 1 \\
-t+3 & \text{if } t>1 \\
\end{array} \right.
\]
Note that when [latex]t = 1[/latex] is substituted into the expression [latex]-t + 3,[/latex]we get 2, so the hole at [latex](1, 2)[/latex] checks.[28]
Example 1.3.11
Example 1.3.11
A popular Fon-i smartphone carrier offers the following smartphone data plan: use any amount of data up to and including 4 gigabytes for $60 per month with an overage charge of $5 per gigabyte. Determine a formula that computes the cost in dollars as a function of using [latex]g[/latex] gigabytes of data per month. Graph your answer.
Solution:
It is clear from context that we are to use the variable [latex]g[/latex] (for gigabytes) as the independent variable. We are asked to compute the cost so it seems natural to name the function [latex]C[/latex]. Hence, we are after a formula for [latex]C(g)[/latex]. Knowing that [latex]g[/latex] represents the amount of data used each month, we must have [latex]g \geq 0[/latex].
In order to get a feel for the formula for [latex]C(g)[/latex], we can choose some specific values for [latex]g[/latex] and determine the cost, [latex]C(g)[/latex]. For example, if we use no data at all, 1 gigabyte of data, or 3.796 gigabytes of data, the cost is the same: $60. Indeed, per the plan, for any amount of data up to and including 4 gigabytes, the cost is $60.
Translating this to function notation means [latex]C(0) = 60[/latex], [latex]C(1) = 60[/latex], [latex]C(3.796) = 60[/latex], and, in general, [latex]C(g) = 60[/latex] for [latex]0 \leq g \leq 4[/latex].
What happens if we use more than 4 gigabytes? Let's say we use 6 gigabytes. Per the plan, we are charged $60 for the first 4 and then $5 for each gigabyte over 4. Using 6 gigabytes means that we are 2 gigabytes over and our overage charge is ($5)(2) = $10. The total cost is the base plus the overages or $60 + $10 = $70. In general, if [latex]g>4[/latex], the expression [latex](g-4)[/latex] computes the amount of data used over 4 gigabytes. Our base plus overage then comes to: [latex]60 + 5(g-4) = 5g+40[/latex].
Putting this together with our previous work, we get
\[ C(g) = \left\{ \begin{array}{rc}
60 & \text{if } 0 \leq g \leq 4 \\
5g+40 & \text{if } g > 4 \\
\end{array} \right.
\]
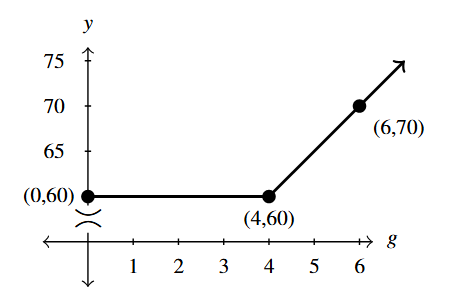
To graph [latex]C[/latex], we graph [latex]y = C(g)[/latex]. For [latex]0 \leq g \leq 4[/latex], we have the horizontal line [latex]y = 60[/latex] from [latex](0,60)[/latex] to [latex](4,60)[/latex].
For [latex]g>4[/latex], we have the line [latex]y = 5g+ 40[/latex]. Even though the inequality [latex]g > 4[/latex] is strict, we nevertheless substitute [latex]g = 4[/latex] into the formula [latex]y = 5g + 40[/latex] and get [latex]y = 60[/latex]. Normally, this would produce a hole at [latex](4, 60)[/latex], but in this case, the point [latex](4, 60)[/latex] is already on the graph from the first piece of the function. Essentially, the point [latex](4,60)[/latex] from [latex]C(g) = 60[/latex] for [latex]0 \leq g \leq 4[/latex] plugs the hole from [latex]C(g) = 5g + 40[/latex] when [latex]g> 4[/latex].
We are graphing a line so we need to plot just one more point to determine the graph. From our work above, we know [latex]C(6) = 70[/latex], so we use [latex](6,70)[/latex] as our second point. Our graph is below. As with the graphs shown from Example 1.2.1, we use [latex]\asymp[/latex] to denote a break in the vertical axis in order to better display the graph.
1.3.4 The Average Rate of Change Of A Function
As mentioned earlier in the section, the concepts of slope and the more general rates of change are important concepts not just in Mathematics, but also in other fields. Many important phenomena are modeled using non-linear functions, and while the rates of change of these functions are not constant, we can sample the function at two points and compute what is known as an average rate of change between them to give some sense as to the function's behavior over that interval.[29]
Let [latex]f[/latex] be a function defined on the interval [latex][a,b].[/latex] The average rate of change of [latex]f[/latex] over [latex][a,b][/latex] is defined as:
\[ \dfrac{\Delta [f(x)]}{\Delta x} = \dfrac{f(b) - f(a)}{b-a} \]
Geometrically, the average rate of change is the slope of the line[30] containing [latex](a, f(a))[/latex] and [latex](b, f(b)).[/latex]
As with Definitions 1.5 and 1.6, the wording in Definition 1.11, while referring to the function [latex]f[/latex], is really making a statement about its outputs [latex]f(x).[/latex]
If [latex]f[/latex] is increasing over [latex](a,b]),[/latex] then the average rate of change will be positive. Likewise, if [latex]f[/latex] is decreasing or constant, the average rate of change will be negative or 0, respectively. (Think about this for a moment.) However, as the next example demonstrates, the converses of these statements aren't always true.[31]
Example 1.3.12
Example 1.3.12.1
The formula [latex]s(t) = -5t^{\,2} + 100t[/latex] for [latex]0 \leq t \leq 20[/latex] gives the height, [latex]s(t)[/latex], measured in feet, of a model rocket above the Moon's surface as a function of the time [latex]t[/latex], in seconds after lift-off.
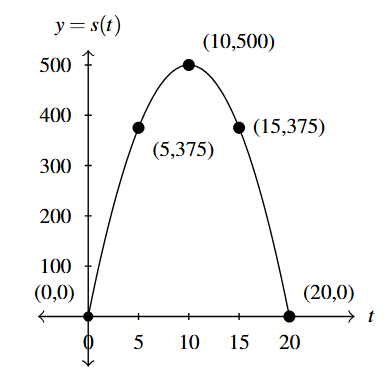
Compute [latex]s(0)[/latex], [latex]s(5)[/latex], [latex]s(10)[/latex], [latex]s(15)[/latex] and [latex]s(20)[/latex] and use these points to graph [latex]y = s(t)[/latex].
Solution:
Compute [latex]s(0)[/latex], [latex]s(5)[/latex], [latex]s(10)[/latex], [latex]s(15)[/latex] and [latex]s(20)[/latex] and use these points to graph [latex]y = s(t)=-5t^{\,2} + 100t.[/latex]
To find [latex]s(0)[/latex], we substitute [latex]t=0[/latex] into the formula for [latex]s(t)[/latex]: [latex]s(0) = -5(0)^2+100(0) = 0[/latex].
Similarly, [latex]s(5) = -5(5)^2+100(5) = -5(25)+500 = -125+500 = 375[/latex].
Continuing, we obtain: [latex]s(10) = 500[/latex], [latex]s(15) = 375[/latex] and [latex]s(20) = 0[/latex].
Using these, we construct a a graph to obtain:
Example 1.3.12.2
The formula [latex]s(t) = -5t^{\,2} + 100t[/latex] for [latex]0 \leq t \leq 20[/latex] gives the height, [latex]s(t)[/latex], measured in feet, of a model rocket above the Moon's surface as a function of the time [latex]t[/latex], in seconds after lift-off.
State the range of [latex]s[/latex] and interpret the extrema, if any exist.
Solution:
State the range of [latex]s[/latex] and interpret the extrema, if any exist.
Projecting the graph to the [latex]y[/latex]-axis, we see that the range of [latex]s[/latex] is [latex][0, 500][/latex] so the minimum of [latex]s[/latex] is 0 and the maximum is 500. This means that the rocket at some point is on the surface of the Moon and reaches its highest altitude of 500 feet above the lunar surface.
Example 1.3.12.3
The formula [latex]s(t) = -5t^{\,2} + 100t[/latex] for [latex]0 \leq t \leq 20[/latex] gives the height, [latex]s(t)[/latex], measured in feet, of a model rocket above the Moon's surface as a function of the time [latex]t[/latex], in seconds after lift-off.
Compute and interpret the [latex]t[/latex]- and [latex]y[/latex]-intercepts.
Solution:
Compute and interpret the [latex]t[/latex]- and [latex]y[/latex]-intercepts.
The first intercept we see is [latex](0, 0)[/latex] which is both a [latex]t[/latex]- and a [latex]y[/latex]-intercept.
Given that [latex]t[/latex] represents the time after lift-off and [latex]y = s(t)[/latex] represents the height above the Moon's surface, the point [latex](0, 0)[/latex] means that the model rocket was launched ([latex]t=0[/latex]) from the Moon's surface ([latex]s(t) = 0[/latex]).
The remaining intercept, [latex](20, 0)[/latex], is another [latex]t[/latex]-intercept. This means that 20 seconds after lift-off ([latex]t=20[/latex]), the model rocket returns to the Moon's surface ([latex]s(t) = 0[/latex]). Said differently, 20 seconds is the time of flight of the model rocket.
Example 1.3.12.4
The formula [latex]s(t) = -5t^{\,2} + 100t[/latex] for [latex]0 \leq t \leq 20[/latex] gives the height, [latex]s(t)[/latex], measured in feet, of a model rocket above the Moon's surface as a function of the time [latex]t[/latex], in seconds after lift-off.
Determine and interpret the interval(s) over which [latex]s[/latex] is increasing, decreasing or constant.
Solution:
Determine and interpret the interval(s) over which [latex]s[/latex] is increasing, decreasing or constant.
Referring to Definition 1.6, [latex]s[/latex] increases over the interval [latex](0, 10)[/latex], because for those values of [latex]t[/latex], as we read from left to right, the graph of the function is rising meaning the [latex]y[/latex] values (hence [latex]s(t)[/latex] values) are getting larger. Thus the model rocket is heading upwards for the first 10 seconds of its flight.
We find that [latex]s[/latex] decreases over the interval [latex](10, 20])[/latex], indicating once it has reached its highest altitude of 500 feet 10 seconds into the flight, the rocket begins to fall back to the surface of the Moon, landing 20 seconds after lift-off.
Example 1.3.12.5
The formula [latex]s(t) = -5t^{\,2} + 100t[/latex] for [latex]0 \leq t \leq 20[/latex] gives the height, [latex]s(t)[/latex], measured in feet, of a model rocket above the Moon's surface as a function of the time [latex]t[/latex], in seconds after lift-off.
Calculate and interpret the average rate of change of [latex]s[/latex] over the intervals [latex][0,5], \; [5,10], \; [10, 20][/latex] and [latex][5, 15].[/latex]
Solution:
Calculate and interpret the average rate of change of [latex]s[/latex] over the intervals [latex][0,5], \; [5,10], \; [10, 20][/latex] and [latex][5, 15].[/latex]
To find the average rate of change of [latex]s[/latex] over the interval [latex][0, 5][/latex] we compute
\[ \begin{array}{rcl} \dfrac{\Delta[s(t)]}{\Delta t} &=& \dfrac{s(5) - s(0)}{5 - 0} \\ & & \\ &=& \dfrac{\text{375 feet}}{\text{5 seconds}} \\& & \\ &=& 75 \text{ feet per second}.\end{array} \]
In other words, the height is increasing at an average rate of 75 feet per second during the first 5 seconds of flight. The rate here is called the average velocity of the rocket over this interval. Velocity differs from speed in that velocity comes with a direction. In this case, a positive velocity indicates that the rocket is traveling upwards, because when [latex]s[/latex] is increasing, the model rocket is climbing higher.
Similarly, the average rate of change of [latex]s[/latex] over the interval [latex][5, 10][/latex] works out to be 25. This means that the average velocity over the next 5 seconds of the flight has slowed to 25 feet per second. The model rocket is still, on average, traveling upwards, albeit more slowly than before.
Over the interval [latex][10, 20],[/latex] the average rate of change of [latex]s[/latex] works out to be[latex]-50.[/latex] This means that, on average, the rocket is falling at a rate of 50 feet per second. The rocket has managed to fall from its highest point 500 feet above the surface of the Moon back to the Moon's surface in 10 seconds so this makes sense.
Last, but not least, the average rate of change of [latex]s[/latex] over [latex][5, 15][/latex] turns out to be 0. This means that the model is the same height above the ground after 5 seconds (375 feet) as it is after 15 seconds.
Geometrically, the average rate of change of a function over an interval can be interpreted as the slope of a secant line. Below is a dotted line containing [latex](0, 0)[/latex] and [latex](5, 375)[/latex] (which has slope 75) along with a dotted line containing the points [latex](5, 375)[/latex] and [latex](10, 500)[/latex] (which has slope 25). Visually, the lines help demonstrate that, while [latex]s[/latex] is increasing over [latex](0, 10)[/latex], the rate of increase is slowing down as [latex]t[/latex] nears 10.
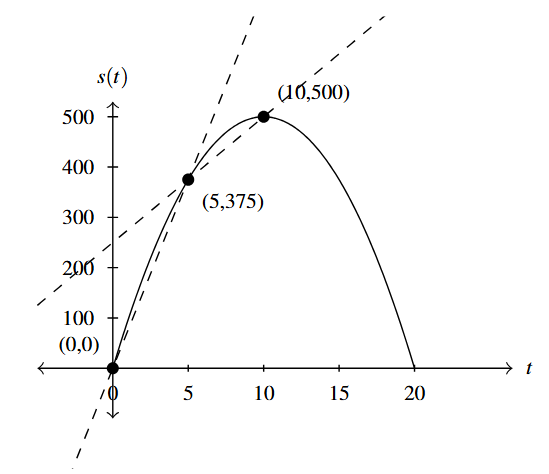
The graph below on the right depicts a dotted line through [latex](10, 500)[/latex] and [latex](20,0)[/latex] indicating a net decrease over that interval. We also have a horizontal line (0 slope) containing the points [latex](5, 375)[/latex] and [latex](15, 375)[/latex], which shows no net change between those two points, despite the fact that the rocket rose to its maximum height then began its descent during the interval [latex](5, 15)[/latex].
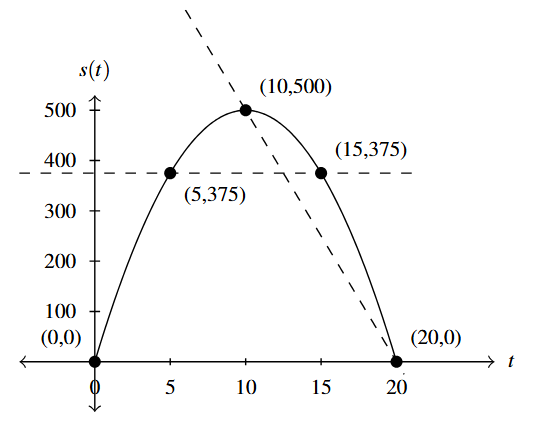
An important lesson from the last example is that average rates of change give us a snapshot of what is happening at the endpoints of an interval, but not necessarily what happens over the course of the interval. Calculus gives us tools to compute slopes at points which correspond to instantaneous rates of changes. While we don't quite have the machinery to properly express these ideas, we can hint at them in the Exercises. Speaking of exercises [latex]\ldots[/latex]
1.3.5 Section Exercises
In Exercises 1 - 10, write both the point-slope form and the slope-intercept form of the line with the given slope which passes through the given point.
- [latex]m = 3, \;\; P(3, -1)[/latex]
- [latex]m = -2, \;\; P(-5, 8)[/latex]
- [latex]m = -1, \;\; P(-7, -1)[/latex]
- [latex]m = \dfrac{2}{3}, \;\; P(-2, 1)[/latex]
- [latex]m = -\dfrac{1}{5}, \;\; P(10, 4)[/latex]
- [latex]m = \dfrac{1}{7}, \;\; P(-1, 4)[/latex]
- [latex]m = 0, \;\; P(3, 117)[/latex]
- [latex]m = -\sqrt{2}, \;\; P(0, -3)[/latex]
- [latex]m = -5, \;\; P(\sqrt{3}, 2\sqrt{3})[/latex]
- [latex]m = 678, \;\; P(-1, -12)[/latex]
In Exercises 11 - 20, write the slope-intercept form of the line which passes through the given points.
- [latex]P(0, 0), \; Q(-3, 5)[/latex]
- [latex]P(-1, -2), \; Q(3, -2)[/latex]
- [latex]P(5, 0), \; Q(0, -8)[/latex]
- [latex]P(3, -5), \; Q(7, 4)[/latex]
- [latex]P(-1,5), \; Q(7, 5)[/latex]
- [latex]P(4, -8), \; Q(5, -8)[/latex]
- [latex]P\left(\dfrac{1}{2}, \dfrac{3}{4} \right), \; Q\left(\dfrac{5}{2}, -\dfrac{7}{4} \right)[/latex]
- [latex]P\left(\dfrac{2}{3}, \dfrac{7}{2} \right), \; Q\left(-\dfrac{1}{3}, \dfrac{3}{2} \right)[/latex]
- [latex]P\left(\sqrt{2}, -\sqrt{2} \right), \; Q\left(-\sqrt{2}, \sqrt{2} \right)[/latex]
- [latex]P\left(-\sqrt{3}, -1 \right), \; Q\left(\sqrt{3}, 1 \right)[/latex]
In Exercises 21 - 26, graph the line. Determine the slope, [latex]y[/latex]-intercept and [latex]x[/latex]-intercept, if any exist.
- [latex]y = 2x - 1[/latex]
- [latex]y = 3 - x[/latex]
- [latex]y=3[/latex]
- [latex]y=0[/latex]
- [latex]y = \dfrac{2}{3} x + \dfrac{1}{3}[/latex]
- [latex]y = \dfrac{1-x}{2}[/latex]
- Graph [latex]3v + 2w = 6[/latex] on both the [latex]vw[/latex]- and [latex]wv[/latex]-axes. What characteristics to both graphs share? What's different?
- Find all of the points on the line [latex]y=2x+1[/latex] which are 4 units from the point [latex](-1,3).[/latex]
In Exercises 29 - 34, you are given a line and a point which is not on that line. Find the line parallel to the given line which passes through the given point.
- [latex]y = 3x + 2, \; P(0, 0)[/latex]
- [latex]y = -6x + 5, \; P(3, 2)[/latex]
- [latex]y = \dfrac{2}{3} x - 7, \; P(6, 0)[/latex]
- [latex]y = \dfrac{4-x}{3}, \; P(1, -1)[/latex]
- [latex]y = 6, \; P(3, -2)[/latex]
- [latex]x=1, \; P(-5,0)[/latex]
In Exercises 35 - 40, you are given a line and a point which is not on that line. Find the line perpendicular to the given line which passes through the given point.
- [latex]y = \dfrac{1}{3}x + 2, \; P(0, 0)[/latex]
- [latex]y = -6x + 5, \; P(3, 2)[/latex]
- [latex]y = \dfrac{2}{3} x - 7, \; P(6, 0)[/latex]
- [latex]y = \dfrac{4-x}{3}, \; P(1, -1)[/latex]
- [latex]y = 6, \; P(3, -2)[/latex]
- [latex]x=1, \; P(-5,0)[/latex]
- We shall now prove that [latex]y = m_{1}x + b_{1}[/latex] is perpendicular to [latex]y = m_{2}x + b_{2}[/latex] if and only if [latex]m_{1} \cdot m_{2} = -1.[/latex] To make our lives easier we shall assume that [latex]m_{1} > 0[/latex] and [latex]m_{2}[/latex] < 0. We can also "move'' the lines so that their point of intersection is the origin without messing things up, so we'll assume [latex]b_{1} = b_{2} = 0.[/latex] (Take a moment with your classmates to discuss why this is okay.) Graphing the lines and plotting the points [latex]O(0, 0)\;, \; P(1, m_{1})\;[/latex] and [latex]Q(1, m_{2})[/latex] gives us the following set up.
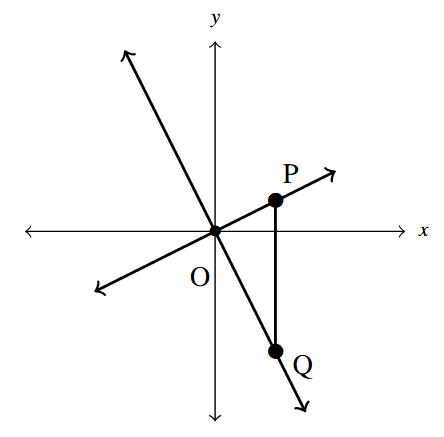
Graph for Exercise 41 The line [latex]y = m_{1}x[/latex] will be perpendicular to the line [latex]y = m_{2}x[/latex] if and only if [latex]\bigtriangleup OPQ[/latex] is a right triangle. Let [latex]d_{1}[/latex] be the distance from [latex]O[/latex] to [latex]P[/latex], let [latex]d_{2}[/latex] be the distance from [latex]O[/latex] to [latex]Q[/latex] and let [latex]d_{3}[/latex] be the distance from [latex]P[/latex] to [latex]Q[/latex]. Use the Pythagorean Theorem to show that [latex]\bigtriangleup OPQ[/latex] is a right triangle if and only if [latex]m_{1} \cdot m_{2} = -1[/latex] by showing [latex]d_{1}^{2} + d_{2}^{2} = d_{3}^2[/latex] if and only if [latex]m_{1} \cdot m_{2} = -1[/latex].
In Exercises 42 - 47, graph the function. Then determine the slope and axis intercepts, if any.
- [latex]f(x) = 2x - 1[/latex]
- [latex]g(t) = 3 - t[/latex]
- [latex]F(w) = 3[/latex]
- [latex]G(s) = 0[/latex]
- [latex]h(t) = \dfrac{2}{3} t + \dfrac{1}{3}[/latex]
- [latex]j(w) = \dfrac{1-w}{2}[/latex]
In Exercises 48 - 51, graph the function. Then determine the domain, range, and axis intercepts, if any.
- [latex]{\displaystyle f(x) = \left\{ \begin{array}{rcl} 4-x & \text{ if } & x \leq 3 \\ 2 & \text{ if } & x > 3\end{array} \right. }[/latex]
- [latex]{\displaystyle g(x) = \left\{ \begin{array}{rcl} 2-x & \text{ if } & x 2 \\x-2 & \text{ if } & x \geq 2\end{array} \right. }[/latex]
- [latex]{\displaystyle F(t) = \left\{ \begin{array}{rcl} -2t - 4 & \text{ if } & t 0 \\3t & \text{ if } & t \geq 0\end{array} \right. }[/latex]
- [latex]{\displaystyle G(t) = \left\{ \begin{array}{rcl} -3 & \text{ if } & t 0 \\2t-3 & \text{ if } & 0 t 3 \\3 & \text{ if } & t > 3\end{array} \right. }[/latex]
- The unit step function is defined as \[ U(t) =\left\{ \begin{array}{rc}
0 & \text{if } t<0 \\
1 & \text{if } t \geq 1 \\
\end{array} \right. \]- Graph [latex]y = U(t).[/latex]
- State the domain and range of [latex]U.[/latex]
- List the interval(s) over which [latex]U[/latex] is increasing, decreasing, and/or constant.
- Write [latex]U(t-2)[/latex] as a piecewise defined function and graph.
In Exercises 53 - 56, find a formula for the function.
-
Graph for Exercise 53 -
Graph for Exercise 54 -
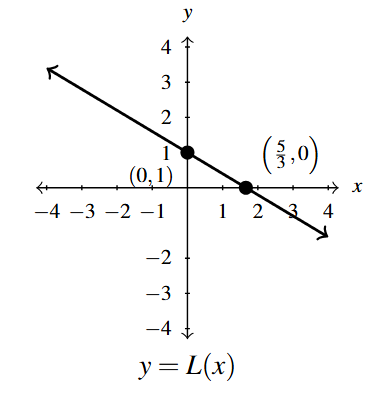
Graph for Exercise 55 -
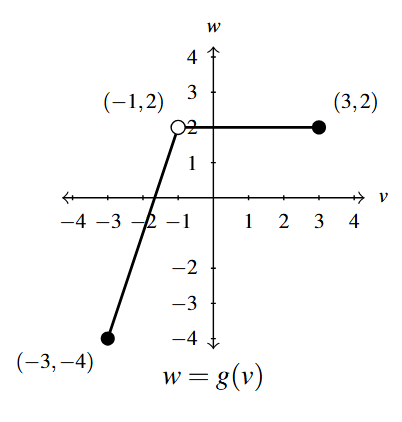
Graph for Exercise 56 - For [latex]n[/latex] copies of the book Me and my Sasquatch, a print on-demand company charges [latex]C(n)[/latex] dollars, where [latex]C(n)[/latex] is determined by the formula \[{\displaystyle C(n) = \left\{ \begin{array}{rcl} 15n & \text{ if } & 1 \leq n \leq 25 \\13.50n & \text{ if } & 25 < n \leq 50 \\12n & \text{ if } & n > 50 \\ \end{array} \right. }\]
- Find and interpret [latex]C(20).[/latex]
- How much does it cost to order 50 copies of the book? What about 51 copies?
- Your answer to 57b should get you thinking. Suppose a bookstore estimates it will sell 50 copies of the book. How many books can, in fact, be ordered for the same price as those 50 copies? (Round your answer to a whole number of books.
- An on-line comic book retailer charges shipping costs according to the following formula \[{\displaystyle S(n) = \left\{ \begin{array}{rcl} 1.5 n + 2.5 & \text{ if } & 1 \leq n \leq 14 \\0 & \text{ if } & n \geq 15
\end{array} \right. }\] where [latex]n[/latex] is the number of comic books purchased and [latex]S(n)[/latex] is the shipping cost in dollars.- What is the cost to ship 10 comic books?
- What is the significance of the formula [latex]S(n) = 0[/latex] for [latex]n \geq 15[/latex]?
- The cost in dollars [latex]C(m)[/latex] to talk [latex]m[/latex] minutes a month on a mobile phone plan is modeled by
\[{\displaystyle C(m) = \left\{ \begin{array}{rcl} 25 & \text{ if } & 0 \leq m \leq 1000 \\25+0.1(m-1000) & \text{ if } & m > 1000
\end{array} \right. }\]- How much does it cost to talk 750 minutes per month with this plan?
- How much does it cost to talk 20 hours a month with this plan?
- Explain the terms of the plan verbally.
- Jeff can walk comfortably at 3 miles per hour. Find an expression for a linear function [latex]d(t)[/latex] that represents the total distance Jeff can walk in [latex]t[/latex] hours, assuming he doesn't take any breaks.
- Carl can stuff 6 envelopes per minute. Find an expression for a linear function [latex]E(t)[/latex] that represents the total number of envelopes Carl can stuff after [latex]t[/latex] hours, assuming he doesn't take any breaks.
- A landscaping company charges $45 per cubic yard of mulch plus a delivery charge of $20. Find an expression for a linear function [latex]C(x)[/latex] which computes the total cost in dollars to deliver [latex]x[/latex] cubic yards of mulch.
- A plumber charges $50 for a service call plus $80 per hour. If she spends no longer than 8 hours a day at any one site, find an expression for a linear function [latex]C(t)[/latex] that computes her total daily charges in dollars as a function of the amount of time spent in hours, [latex]t[/latex] at any one given location.
- A salesperson is paid $200 per week plus 5% commission on her weekly sales of [latex]x[/latex] dollars. Find an expression for a linear function [latex]W(x)[/latex] which computes her total weekly pay in dollars as a function of [latex]x.[/latex] What must her weekly sales be in order for her to earn $475.00 for the week?
- An on-demand publisher charges $22.50 to print a 600 page book and $15.50 to print a 400 page book. Find an expression for a linear function which models the cost of a book in dollars [latex]C(p)[/latex] as a function of the number of pages [latex]p.[/latex] Find and interpret both the slope of the linear function and [latex]C(0)[/latex].
- The Topology Taxi Company charges $2.50 for the first fifth of a mile and 45 cents for each additional fifth of a mile. Find an expression for a linear function which models the taxi fare [latex]F(m)[/latex] as a function of the number of miles driven, [latex]m.[/latex] Find and interpret both the slope of the linear function and [latex]F(0).[/latex]
- Water freezes at [latex]0^{\circ}[/latex] Celsius and [latex]32^{\circ}[/latex] Fahrenheit and it boils at [latex]100^{\circ}[/latex]C and [latex]212^{\circ}[/latex]F.
- Find an expression for a linear function [latex]F(T)[/latex] that computes temperature in the Fahrenheit scale as a function of the temperature [latex]T[/latex] given in degrees Celsius. Use this function to convert [latex]20^{\circ}[/latex]C into Fahrenheit.
- Find an expression for a linear function [latex]C(T)[/latex] that computes temperature in the Celsius scale as a function of the temperature [latex]T[/latex] given in degrees Fahrenheit. Use this function to convert [latex]110^{\circ}[/latex]F into Celsius.
- Is there a temperature [latex]T[/latex] such that [latex]F(T) = C(T)[/latex]?
- Legend has it that a bull Sasquatch in rut will howl approximately 9 times per hour when it is [latex]40^{\circ}F[/latex] outside and only 5 times per hour if it's [latex]70^{\circ}F.[/latex] Assuming that the number of howls per hour, [latex]N[/latex], can be represented by a linear function of temperature Fahrenheit, find the number of howls per hour he'll make when it's only [latex]20^{\circ}F[/latex] outside. What troubles do you encounter when trying to determine a reasonable applied domain?
- Economic forces have changed the cost function for PortaBoys to [latex]C(x) = 105x + 175[/latex]. Rework Example 1.3.8 with this new cost function.
- In response to the economic forces in Exercise 69 above, the local retailer sets the selling price of a PortaBoy at $250. Remarkably, 30 units were sold each week. When the systems went on sale for $220, 40 units per week were sold. Rework Example 1.3.9 with this new data.
- A local pizza store offers medium two-topping pizzas delivered for $6.00 per pizza plus a $1.50 delivery charge per order. On weekends, the store runs a game day special: if six or more medium two-topping pizzas are ordered, they are $5.50 each with no delivery charge. Write a piecewise-defined linear function which calculates the cost in dollars [latex]C(p)[/latex] of [latex]p[/latex] medium two-topping pizzas delivered during a weekend.
- A restaurant offers a buffet which costs $15 per person. For parties of 10 or more people, a group discount applies, and the cost is $12.50 per person. Write a piecewise-defined linear function which calculates the total bill [latex]T(n)[/latex] of a party of [latex]n[/latex] people who all choose the buffet.
- A mobile plan charges a base monthly rate of $10 for the first 500 minutes of air time plus a charge of 15 cents for each additional minute. Write a piecewise-defined linear function which calculates the monthly cost in dollars [latex]C(m)[/latex] for using [latex]m[/latex] minutes of air time.
HINT: You may wish to refer to number 59 for inspiration. - The local pet shop charges 12 cents per cricket up to 100 crickets, and 10 cents per cricket thereafter. Write a piecewise-defined linear function which calculates the price in dollars [latex]P(c)[/latex] of purchasing [latex]c[/latex] crickets.
- The cross-section of a swimming pool is at the top of the next page. Write a piecewise-defined linear function which describes the depth of the pool, [latex]D[/latex] (in feet) as a function of:
- the distance (in feet) from the edge of the shallow end of the pool, [latex]d.[/latex]
- the distance (in feet) from the edge of the deep end of the pool, [latex]s.[/latex]
- Graph each of the functions in (a) and (b). Discuss with your classmates how to transform one into the other and how they relate to the diagram of the pool.
Diagram for Exercise 75
- The function defined by [latex]I(x) = x[/latex] is called the Identity Function. Thinking from a procedural perspective, explain a possible origin of this name.
- Why must the graph of a function [latex]y = f(x)[/latex] have at most one [latex]y[/latex]-intercept?
HINT: Consider what would happen graphically if there were more than one [latex]\ldots[/latex] - Why is a discussion of vertical lines omitted when discussing functions?
- Find a formula for the [latex]x[/latex]-intercept of the graph of [latex]f(x) = mx + b.[/latex] Assume [latex]m \neq 0[/latex].
- Suppose [latex](c,0)[/latex] is the [latex]x[/latex]-intercept of a linear function [latex]f.[/latex] Use the point-slope form of a liner function, Equation 1.8 to show [latex]f(x) = m(x-c).[/latex] This is the slope [latex]x[/latex]-intercept form of the linear function.
- Prove that for all linear functions [latex]L[/latex] with slope 3, [latex]L(120) = L(100) + 60.[/latex]
In Exercises 82 - 87, compute the average rate of change of the function over the specified interval.
- [latex]f(x) = x^{3}, \; [-1, 2][/latex]
- [latex]g(x) = \dfrac{1}{x}, \; [1, 5][/latex]
- [latex]f(t) = \sqrt{t}, \; [0, 16][/latex]
- [latex]g(t) = x^{2}, \; [-3, 3][/latex]
- [latex]F(s) = \dfrac{s + 4}{s - 3}, \; [5, 7][/latex]
- [latex]G(s) = 3s^{2} + 2s - 7, \; [-4, 2][/latex]
- The height of an object dropped from the roof of a building is modeled by: [latex]h(t) = -16t^2 + 64,[/latex] for [latex]0 \leq t \leq 2.[/latex] Here, [latex]h(t)[/latex] is the height of the object off the ground in feet [latex]t[/latex] seconds after the object is dropped. Find and interpret the average rate of change of [latex]h[/latex] over the interval [latex][0,2].[/latex]
- Using data from Bureau of Transportation Statistics, the average fuel economy [latex]F(t)[/latex] in miles per gallon for passenger cars in the US can be modeled by [latex]F(t) = -0.0076t^2+0.45t + 16[/latex], [latex]0 \leq t \leq 28[/latex], where [latex]t[/latex] is the number of years since 1980. Find and interpret the average rate of change of [latex]F[/latex] over the interval [latex][0,28][/latex].
- The temperature [latex]T(t)[/latex] in degrees Fahrenheit [latex]t[/latex] hours after 6 AM is given by: \[ T(t) = -\dfrac{1}{2} t^2 + 8t+32, \quad 0 \leq t \leq 12\]
- Find and interpret [latex]T(4)[/latex], [latex]T(8)[/latex] and [latex]T(12).[/latex]
- Find and interpret the average rate of change of [latex]T[/latex] over the interval [latex][4,8].[/latex]
- Find and interpret the average rate of change of [latex]T[/latex] from [latex]t=8[/latex] to [latex]t=12.[/latex]
- Find and interpret the average rate of temperature change between 10 AM and 6 PM.
- Suppose [latex]C(x) = x^2-10x+27[/latex] represents the costs, in hundreds, to produce [latex]x[/latex] thousand pens. Find and interpret the average rate of change as production is increased from making 3000 to 5000 pens.
- Recall from Example 1.3.12 the formula [latex]s(t) = -5t^2+100t[/latex] for [latex]0 \leq t \leq 20[/latex] gives the height, [latex]s(t)[/latex], measured in feet, of a model rocket above the Moon's surface as a function of the time after lift-off, [latex]t[/latex], in seconds.
- Find and interpret the average rate of change of [latex]s[/latex] over the following intervals:
- [latex][14.9, 15][/latex]
- [latex][15, 15.1][/latex]
- [latex][14.99, 15][/latex]
- [latex][15, 15.01][/latex]
- What value does the average rate of change appear to be approaching as the interval shrinks closer to the value [latex]t=15[/latex]?
- Find the equation of the line containing [latex](15, 375)[/latex] with slope [latex]m = -50[/latex] and graph it along with [latex]s[/latex] on the same set of axes using a graphing utility. What happens as you zoom in near [latex](15, 375)?[/latex]
- Find and interpret the average rate of change of [latex]s[/latex] over the following intervals:
- Show the average rate of change of a function of the form [latex]f(x) = mx+b[/latex] over any interval is [latex]m[/latex].
- Why doesn't the graph of the vertical line [latex]x = b[/latex] in the [latex]xy[/latex]-plane represent [latex]y[/latex] as a function of [latex]x[/latex]?
- With help from a graphing utility, graph the following pairs of functions on the same set of axes:[32]
- [latex]f(x) = 2-x[/latex] and [latex]g(x) = \lfloor 2-x \rfloor[/latex]
- [latex]f(x) = x^2-4[/latex] and [latex]g(x) = \lfloor x^2 -4\rfloor[/latex]
- [latex]f(x) = x^3[/latex] and [latex]g(x) = \lfloor x^3 \rfloor[/latex]
- [latex]f(x) = \sqrt{x}-4[/latex]and [latex]g(x) = \lfloor \sqrt{x} -4 \rfloor[/latex]
Choose more functions [latex]f(x)[/latex] and graph [latex]y = f(x)[/latex] alongside [latex]y = \lfloor f(x) \rfloor[/latex] until you can explain how, in general, one would obtain the graph of [latex]y = \lfloor f(x) \rfloor[/latex] given the graph of [latex]y = f(x).[/latex]
- The Lagrange Interpolate function [latex]L[/latex] for two points [latex](x_{0}, y_{0})[/latex] and [latex](x_{1}, y_{1})[/latex] where [latex]x_{0} \neq x_{1}[/latex] is given by: \[L(x) = y_{0} \dfrac{x - x_{1}}{x_{0} - x_{1}}+ y_{1}\dfrac{x - x_{0}}{x_{1} - x_{0}}\]
- For each of the following pairs of points, find [latex]L(x)[/latex] using the formula above and verify each of the points lies on the graph of [latex]y = L(x).[/latex]
- [latex](-1,3), \; (2,3)[/latex]
- [latex](-3,-2), \; (5,-2)[/latex]
- [latex](-3,-2), \; (0,1)[/latex]
- [latex](-1,5), \; (2,-1)[/latex]
- Verify that, in general, [latex]L(x_{0}) = y_{0}[/latex] and [latex]L(x_{1}) = y_{1}.[/latex]
- Show the point-slope form of a linear function, Equation 1.8 is equivalent to the formula given for [latex]L(x)[/latex] after making the identifications: [latex]f(x_{0}) = y_{0}[/latex] and [latex]m = \dfrac{y_{1} - y_{0}}{x_{1} - x_{0}}.[/latex]
- For each of the following pairs of points, find [latex]L(x)[/latex] using the formula above and verify each of the points lies on the graph of [latex]y = L(x).[/latex]
Section 1.3 Exercise Answers can be found in the Appendix.
- See www.mathforum.org or www.mathworld.wolfram.com for discussions on this topic. ↵
- That is, as we increase the [latex]x[/latex]-values [latex]\ldots[/latex] ↵
- Some authors use the unfortunate moniker no slope when a slope is undefined. It's easy to confuse the notions of no slope with slope of 0. For this reason, we will describe slopes of vertical lines as undefined. ↵
- Here we have [latex]y_{0}[/latex] as the constant whereas in the Equation 1.4 we used the letter [latex]b.[/latex] The form [latex]y =[/latex] constant is what matters. ↵
- Hopefully? ↵
- We can verify this algebraically by setting [latex]x=0[/latex] in the equation [latex]y=mx+b[/latex] and obtaining [latex]y = b[/latex]. ↵
- Recall, [latex]x = x^{1}[/latex], [latex]y = y^{1}[/latex], etc. ↵
- You may recall, that this is the [latex]x[/latex]-intercept of the line. ↵
- Lines missing points - even one - usually belie some algebraic pathology which we'll discuss in more detail in Chapter 3. ↵
- Well, at least in Euclidean Geometry \dots ↵
- Please ask your instructor if lying on the line counts as being symmetric about the line or not. ↵
- It gets much weirder than that as we explore other more complicated functions. The key is to pay attention to the precision in the definitions of the terms involved in the discussion. Stay tuned! ↵
- See our discussion about holes in graphs in Example 1.2.6 in Section 1.2. ↵
- The domain of [latex]p[/latex] is [latex][0, \infty)[/latex] by definition, even though few 327 year olds are out and about these days. ↵
- The use of the letter [latex]\mathbb{Z}[/latex] for the integers is ostensibly because the German word zahlen means to count. ↵
- The first half of any introductory Calculus course is about slope. ↵
- More specifically, if [latex](x_{0}, y_{0})[/latex] and [latex](x_{1}, y_{1})[/latex] are two distinct points in the plane, then [latex]\Delta x = x_{1} - x_{0}[/latex] and [latex]\Delta y = y_{1} - y_{0}[/latex]. ↵
- Actually, it makes no sense to produce a fractional part of a game system, either, which we'll discuss later in this example. ↵
- This is an example of using a continuous variable to model a discrete scenario. Contrast this with the discussion following Example 1.2.1 in Section 1.2. ↵
- The cost to produce just one more item is called the marginal cost. The difference between variable and marginal costs in this case are the units used: the variable cost is $80 per Portaboy whereas the marginal cost is simply $80. ↵
- In the case [latex]x_{0} = 0[/latex], this formula reduces to [latex]C(x) = C(0) + 80(x - 0) = 150 + 80x = 80x + 150[/latex]. To show the formula in general, consider [latex]C(x_{0}) = 80x_{0} + 150 \ldots [/latex] ↵
- In other words, the slope-intercept form of a line is just a special case of the point-slope form. ↵
- Recall that the bar over the 6 indicates that the decimal repeats. ↵
- ignoring returns, that is. ↵
- We'll discuss these sorts of connections in greater depth in Section 1.4. ↵
- It may seem counter-intuitive to express price as a function of demand. Shouldn't the price determine how many systems people will buy? We will address this issue later. ↵
- We actually could use the point [latex](1, 2)[/latex] to find the equation of the line containing [latex](1, 2)[/latex] and, say [latex](3, 0)[/latex], which is [latex]y = -t + 3[/latex]. It's just that the graph of [latex]L(t)[/latex] and the line [latex]y = -t + 3[/latex] only agree for [latex]t > 1[/latex], so it would be incorrect to write [latex]L(1) = 2[/latex]. ↵
- Alternatively, for [latex]t[/latex] values larger than 1 but getting closer and closer to 1, [latex]L(t) \approx 2.[/latex] ↵
- We are basically pretending that the function is linear on a short interval to see what we can say about its behavior. ↵
- This line is called a secant line. ↵
- For example, the average rate of change over an interval could be positive yet the function could decrease over part of that interval and then increase on a different part. ↵
- See Example 1.3.7 for the definition of [latex]\lfloor x \rfloor[/latex]. ↵
The equation for a line when given the slope and any point on the line.
A point on a graph which is also on the x-axis.
A point on a graph which is also on the y-axis.
A function which returns the same values regardless of the input.
A function where the rule to determine outputs, not just the value of the output, changes depending on the inputs.
A function of the form f(x)=mx+b, assuming m is not equal to zero.
The average rate of change of a function between two points is the change in the function values over the corresponding change in the independent variables.

