Section 5.1 Answers
- Answers May Vary
- Answers May Vary
- Answers May Vary
- Answers May Vary
- Answers May Vary
- Answers May Vary
- Answers May Vary
- Answers May Vary
- [latex]f^{-1}(x) = \dfrac{x + 2}{6}[/latex]
- [latex]f^{-1}(x) = 42-x[/latex]
- [latex]g^{-1}(t) = 3t-10[/latex]
- [latex]g^{-1}(t) = -\frac{5}{3} t + \frac{1}{3}[/latex]
- [latex]f^{-1}(x) = \frac{1}{3}(x-5)^2+\frac{1}{3}[/latex], [latex]x \geq 5[/latex]
- [latex]f^{-1}(x) = (x - 2)^{2} + 5, \; x \leq 2[/latex]
- [latex]g^{-1}(t) = \frac{1}{9}(t+4)^2+1[/latex], [latex]t \geq -4[/latex]
- [latex]g^{-1}(t) = \frac{1}{8}(t-1)^2-\frac{5}{2}[/latex], [latex]t \leq 1[/latex]
- [latex]f^{-1}(x) = \frac{1}{3} x^{5} + \frac{1}{3}[/latex]
- [latex]f^{-1}(x) = -(x-3)^3+2[/latex]
- [latex]g^{-1}(t) = 5 + \sqrt{t+25}[/latex]
- [latex]g^{-1}(t) = -\sqrt{\frac{t + 5}{3}} - 4[/latex]
- [latex]f^{-1}(x) = 3 - \sqrt{x+4}[/latex]
- [latex]f^{-1}(x) =-\frac{\sqrt{x}+1}{2}[/latex], [latex]x > 1[/latex]
- [latex]g^{-1}(t) = \dfrac{4t-3}{t}[/latex]
- [latex]g^{-1}(t) = \dfrac{t}{3t+1}[/latex]
- [latex]f^{-1}(x) = \dfrac{4x+1}{2-3x}[/latex]
- [latex]f^{-1}(x) = \dfrac{6x + 2}{3x - 4}[/latex]
- [latex]g^{-1}(t) = \dfrac{-3t - 2}{t + 3}[/latex]
- [latex]g^{-1}(t) = \dfrac{t-2}{2t-1}[/latex]
- .
- None of the first coordinates of the ordered pairs in [latex]F[/latex] are repeated, so [latex]F[/latex] is a function and none of the second coordinates of the ordered pairs of [latex]F[/latex] are repeated, so [latex]F[/latex] is one-to-one. [latex]F^{-1} = \{ (0,0), (1,1), (-1,2), (2,3), (-2,4), (3,5), (-3,6) \}[/latex]
- Because of the [latex]\ldots[/latex] it is helpful to determine a formula for the matching. For the even numbers [latex]n[/latex], [latex]n = 0, 2, 4, \ldots[/latex], the ordered pair [latex]\left(n, -\frac{n}{2} \right)[/latex] is in [latex]G[/latex]. For the odd numbers [latex]n = 1, 3, 5, \ldots[/latex], the ordered pair [latex]\left(n, \frac{n+1}{2} \right)[/latex] is in [latex]G[/latex]. Hence, given any input to [latex]G[/latex], [latex]n[/latex], whether it be even or odd, there is only one output from [latex]G[/latex], either [latex]-\frac{n}{2}[/latex] or [latex]\frac{n+1}{2}[/latex], both of which are functions of [latex]n[/latex]. To show [latex]G[/latex] is one to one, we note that if the output from [latex]G[/latex] is 0 or less, then it must be of the form [latex]-\frac{n}{2}[/latex] for an even number [latex]n[/latex]. Moreover, if [latex]-\frac{n}{2} = -\frac{m}{2}[/latex], then [latex]n = m[/latex]. In the case we are looking at outputs from [latex]G[/latex] which are greater than [latex]0[/latex], then it must be of the form [latex]\frac{n+1}{2}[/latex] for an odd number [latex]n[/latex]. In this, too, if [latex]\frac{n+1}{2} = \frac{m+1}{2}[/latex], then [latex]n = m[/latex]. Hence, in any case, if the outputs from [latex]G[/latex] are the same, then the inputs to [latex]G[/latex] had to be the same so [latex]G[/latex] is one-to-one and [latex]G^{-1} = \{ (0,0), (1,1), (-1,2), (2,3), (-2,4), (3,5), (-3,6), \ldots \}[/latex]
- To show [latex]P[/latex] is a function we note that if we have the same inputs to [latex]P[/latex], say [latex]2t^{5} = 2u^{5}[/latex], then [latex]t = u[/latex]. Hence the corresponding outputs, [latex]2t-1[/latex] and [latex]3u-1[/latex], are equal, too. To show [latex]P[/latex] is one-to-one, we note that if we have the same outputs from [latex]P[/latex], [latex]3t-1 = 3u-1[/latex], then [latex]t = u[/latex]. Hence, the corresponding inputs [latex]2t^5[/latex] and [latex]2u^5[/latex] are equal, too. Hence [latex]P[/latex] is one-to-one and [latex]P^{-1} = \{ (3t-1, 2t^5) \, | \, t \text{ is a real number.} \}[/latex]
- To show [latex]Q[/latex] is a function, we note that if we have the same inputs to [latex]Q[/latex], say [latex]n = m[/latex], then the outputs from [latex]Q[/latex], namely [latex]n^2[/latex] and [latex]m^2[/latex] are equal. To show [latex]Q[/latex] is one-to-one, we note that if we get the same output from [latex]Q[/latex], namely [latex]n^2 = m^2[/latex], then [latex]n = \pm m[/latex]. However because [latex]n[/latex] and [latex]m[/latex] are \textit{natural} numbers, both [latex]n[/latex] and [latex]m[/latex] are positive so [latex]n = m[/latex]. Hence [latex]Q[/latex] is one-to-one and [latex]Q^{-1} = \{ (n^2, n) \, | \, n \, \text{ is a \textit{natural} number.} \}[/latex].
- [latex]y = f^{-1}(x)[/latex]. Asymptote: [latex]x = 0[/latex]
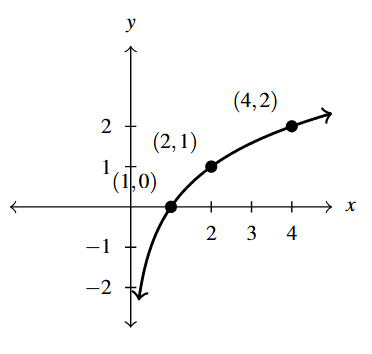
Answer to Exercise 30 - [latex]y = g^{-1}(t)[/latex]. Asymptote: [latex]y=2[/latex]
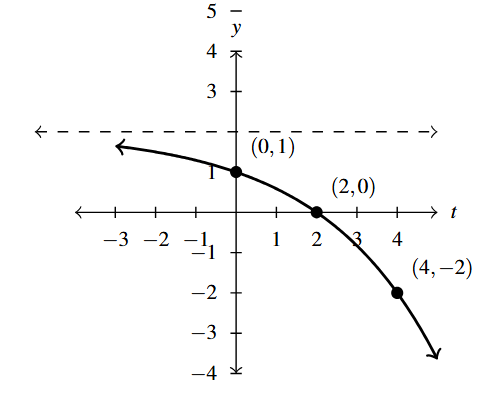
Answer to Exercise 31 - [latex]y = S^{-1}(t)[/latex]. Domain [latex][-3,3][/latex]
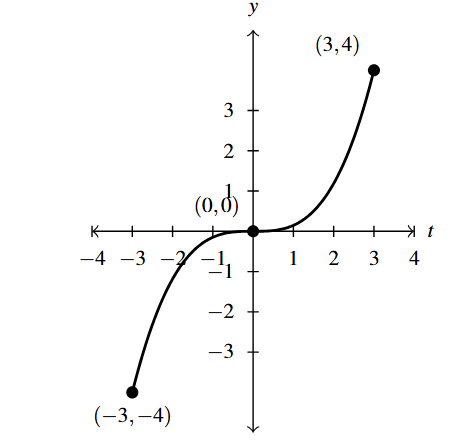
Answer to Exercise 32 - [latex]y = R^{-1}(s)[/latex]. Asymptotes: [latex]s = \pm 3[/latex]
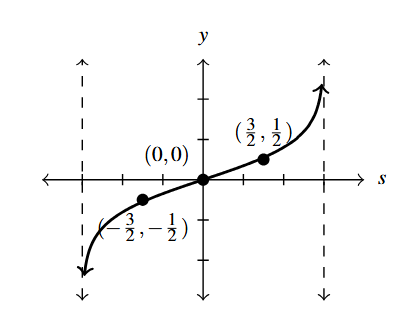
Answer to Exercise 33 - .
- [latex]p^{-1}(x) = \frac{450-x}{15}[/latex]. The domain of [latex]p^{-1}[/latex] is the range of [latex]p[/latex] which is [latex][0,450][/latex]
- [latex]p^{-1}(105) = 23[/latex]. This means that if the price is set to [latex]\$105[/latex] then [latex]23[/latex] dOpis will be sold.
- [latex]\left(P\circ p^{-1}\right)(x) = -\frac{1}{15} x^2 + \frac{110}{3} x - 5000[/latex], [latex]0 \leq x \leq 450[/latex]. The graph of [latex]y = \left(P\circ p^{-1}\right)(x)[/latex] is a parabola opening downwards with vertex [latex]\left(275, \frac{125}{3}\right) \approx (275, 41.67)[/latex]. This means that the maximum profit is a whopping [latex]\$41.67[/latex] when the price per dOpi is set to [latex]\$275[/latex]. At this price, we can produce and sell [latex]p^{-1}(275) = 11.\overline{6}[/latex] dOpis. We cannot sell part of a system, so we need to adjust the price to sell either [latex]11[/latex] dOpis or [latex]12[/latex] dOpis. We find [latex]p(11) = 285[/latex] and [latex]p(12) = 270[/latex], which means we set the price per dOpi at either [latex]\$285[/latex] or [latex]\$270[/latex], respectively. The profits at these prices are [latex]\left(P\circ p^{-1}\right)(285) = 35[/latex] and [latex]\left(P\circ p^{-1}\right)(270) = 40[/latex], so it looks as if the maximum profit is [latex]\$40[/latex] and it is made by producing and selling [latex]12[/latex] dOpis a week at a price of [latex]\$270[/latex] per dOpi.
- Answers May Vary
- Given that [latex]f(0) = 1[/latex], we have [latex]f^{-1}(1) = 0[/latex]. Similarly [latex]f^{-1}(5) = 1[/latex] and [latex]f^{-1}(-3) = -1[/latex]
- Answers May Vary
- b. If [latex]b =0[/latex], then [latex]m = \pm 1[/latex]. If [latex]b \neq 0[/latex], then [latex]m = -1[/latex] and [latex]b[/latex] can be any real number.
Section 5.2 Answers
-
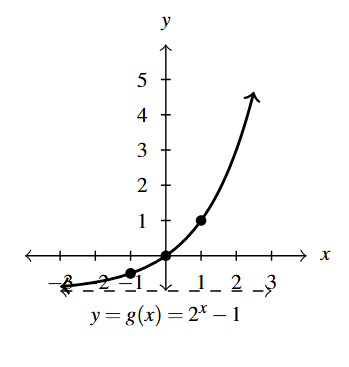
Answer to Exercise 1 - Domain of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-1, \infty)[/latex]
- Points: [latex]\left(-1, -\frac{1}{2} \right)[/latex], [latex](0,0)[/latex], [latex](1,1)[/latex]
- Asymptote: [latex]y = -1[/latex]
-
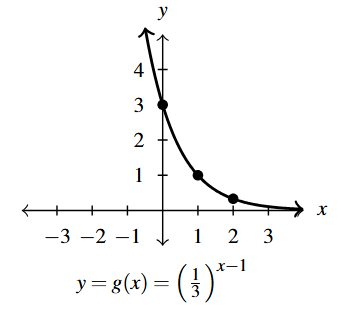
Answer to Exercise 2 - Domain of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](0, \infty)[/latex]
- Points: [latex](0,3)[/latex], [latex](1,1)[/latex], [latex]\left(2, \frac{1}{3} \right)[/latex]
- Asymptote: [latex]y = 0[/latex]
-
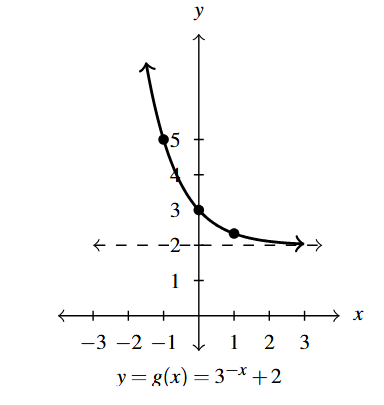
Answer to Exercise 3 - Domain of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](2, \infty)[/latex]
- Points: [latex]\left(1, \frac{7}{3} \right)[/latex], [latex](0,3)[/latex], [latex](-1,5)[/latex]
- Asymptote: [latex]y = 2[/latex]
-
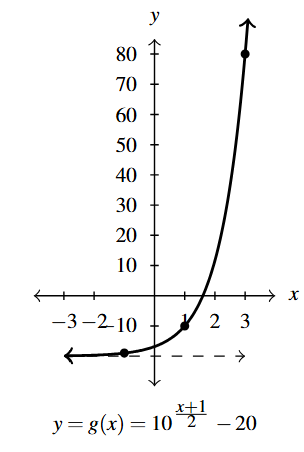
Answer to Exercise 4 - Domain of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-20, \infty)[/latex]
- Points: [latex]\left(-1,-19 \right)[/latex], [latex](1,-10)[/latex], [latex](3,80)[/latex]
- Asymptote: [latex]y = -20[/latex]
-
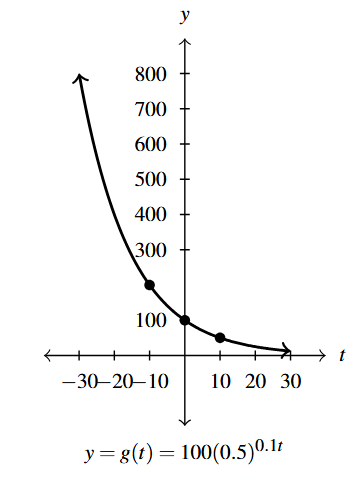
Answer to Exercise 5 - Domain of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](0, \infty)[/latex]
- Points: [latex](-10, 200)[/latex], [latex](0, 100)[/latex], [latex](10, 50)[/latex]
- Asymptote: [latex]y = 0[/latex]
-
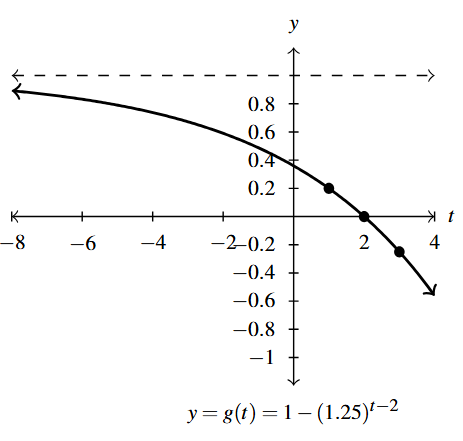
Answer to Exercise 6 - Domain of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-\infty, 1)[/latex]
- Points: [latex](1, 0.2)[/latex], [latex](2,0)[/latex], [latex](3,-0.25)[/latex]
- Asymptote: [latex]y = 1[/latex]
-
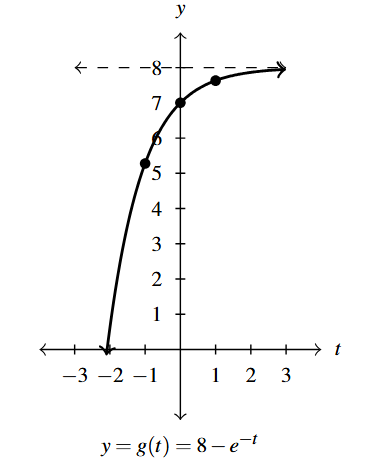
Answer to Exercise 7 - Domain of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-\infty, 8)[/latex]
- Points: [latex]\left(1, 8-e^{-1} \right) \approx (1, 7.63)[/latex],
- [latex](0,7)[/latex], [latex]\left(-1, 8-e \right) \approx (1,5.28)[/latex]
- Asymptote: [latex]y = 8[/latex]
-
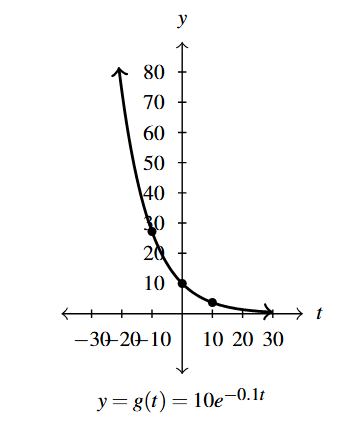
Answer to Exercise 8 - Domain of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](0, \infty)[/latex]
- Points: [latex]\left(10, 10e^{-1} \right) \approx (10, 3.68)[/latex]
- [latex](0,10)[/latex], [latex]\left(-10, 10e \right) \approx (-10, 27.18)[/latex]
- Asymptote: [latex]y = 0[/latex]
- [latex]F(x) = 2^{x+1}-3[/latex]
- [latex]F(x) = -2^{-x} + 3[/latex]
- [latex]F(x) = 2^{2x-6}[/latex]
- [latex]F(x) =3 \cdot 2^{-2x}[/latex]
- Knowing [latex]2 = 4^{\frac{1}{2}}[/latex], one way to obtain the formulas for [latex]G(x)[/latex] is to use properties of exponents. For example, [latex]F(x) = 2^{x+1}-3 = \left(4^{\frac{1}{2}}\right)^{x+1} -3 = 4^{\frac{1}{2}(x+1)} - 3 = 4^{\frac{1}{2} x + \frac{1}{2}} - 3[/latex]. In order, the formulas for [latex]G(x)[/latex] are:
- [latex]G(x) = 4^{\frac{1}{2}x+\frac{1}{2}}-3[/latex]
- [latex]G(x) = -4^{-\frac{1}{2} x} + 3[/latex]
- [latex]G(x) = 4^{x-3}[/latex]
- [latex]G(x) =3 \cdot 4^{-x}[/latex]
- Answers May Vary
- One solution is [latex]g(x) = e^{-x}[/latex] and [latex]h(x) = 1[/latex].
- One solution is [latex]g(x) = e^{2x}[/latex] and [latex]h(x) = x[/latex].
- One solution is [latex]g(t) = t^2[/latex] and [latex]h(t) = e^{-t}[/latex].
- One solution is [latex]f(x) = e^{x} - e^{-x}[/latex] and [latex]g(x) = e^{x}+e^{-x}[/latex].
- One solution is [latex]f(x) = -x^2[/latex] and [latex]g(x) = e^{x}[/latex].
- One solution is [latex]f(x) = e^{2x} -1[/latex] and [latex]g(x) = \sqrt{x}[/latex].
Section 5.3 Answers
- [latex]\log_{2}(8) = 3[/latex]
- [latex]\log_{5}\left(\frac{1}{125}\right) = -3[/latex]
- [latex]\log_{4}(32) = \frac{5}{2}[/latex]
- [latex]\log_{\frac{1}{3}}(9) = -2[/latex]
- [latex]\log_{\frac{4}{25}}\left(\frac{5}{2}\right) = -\frac{1}{2}[/latex]
- [latex]\log(0.001) = -3[/latex]
- [latex]\ln(1) = 0[/latex]
- [latex]5^{2} = 25[/latex]
- [latex](25)^{\frac{1}{2}} = 5[/latex]
- [latex]3^{-4} = \frac{1}{81}[/latex]
- [latex]\left(\frac{4}{3} \right)^{-1} = \frac{3}{4}[/latex]
- [latex]10^{2} = 100[/latex]
- [latex]10^{-1} = 0.1[/latex]
- [latex]e^{1} = e[/latex]
- [latex]e^{-\frac{1}{2}} = \frac{1}{\sqrt{e}}[/latex]
- [latex]\log_{3} (27) = 3[/latex]
- [latex]\log_{6} (216) = 3[/latex]
- [latex]\log_{2} (32) = 5[/latex]
- [latex]\log_{6} \left( \frac{1}{36} \right) = -2[/latex]
- [latex]\log_{8} (4) = \frac{2}{3}[/latex]
- [latex]\log_{36} (216) = \frac{3}{2}[/latex]
- [latex]\log_{\frac{1}{5}} (625) = -4[/latex]
- [latex]\log_{\frac{1}{6}} (216) = -3[/latex]
- [latex]\log_{36} (36)=1[/latex]
- [latex]\log \frac{1}{1000000} = -6[/latex]
- [latex]\log(0.01) = -2[/latex]
- [latex]\ln\left(e^3\right) = 3[/latex]
- [latex]\log_{4} (8) = \frac{3}{2}[/latex]
- [latex]\log_{6} (1) = 0[/latex]
- [latex]\log_{13} \left(\sqrt{13}\right) = \frac{1}{2}[/latex]
- [latex]\log_{36} \left(\sqrt[4]{36}\right) = \frac{1}{4}[/latex]
- [latex]7^{\log_{7} (3)} = 3[/latex]
- [latex]36^{\log_{36}(216)} = 216[/latex]
- [latex]\log_{36} \left(36^{216}\right) = 216[/latex]
- [latex]\ln(e^{5}) = 5[/latex]
- [latex]\log \left(\sqrt[9]{10^{11}}\right) = \frac{11}{9}[/latex]
- [latex]\log\left( \sqrt[3]{10^5} \right) = \frac{5}{3}[/latex]
- [latex]\ln \left( \frac{1}{\sqrt{e}}\right) = -\frac{1}{2}[/latex]
- [latex]\log_{5} \left(3^{\log_{3} 5}\right) = 1[/latex]
- [latex]\log\left(e^{\ln(100)}\right) = 2[/latex]
- [latex]\log_{2}\left(3^{-\log_{3}(2)}\right) = -1[/latex]
- [latex]\ln\left(42^{6\log(1)}\right) = 0[/latex]
- [latex](-\infty, \infty)[/latex]
- [latex](-2, \infty)[/latex]
- [latex](5, \infty)[/latex]
- [latex](-\infty, -6) \cup (-3, \infty)[/latex]
- [latex](-2, -1) \cup (1, \infty)[/latex]
- [latex](-6,-3) \cup (5, \infty)[/latex]
- [latex](4, 7)[/latex]
- [latex](5, \infty)[/latex]
- [latex](-\infty, \infty)[/latex]
- [latex][1, \infty)[/latex]
- [latex](-\infty, -7) \cup (1, \infty)[/latex]
- [latex](13, \infty)[/latex]
- [latex](0, 125) \cup (125, \infty)[/latex]
- No domain
- [latex](-\infty, -3) \cup \left(\frac{1}{2}, 2\right)[/latex]
-
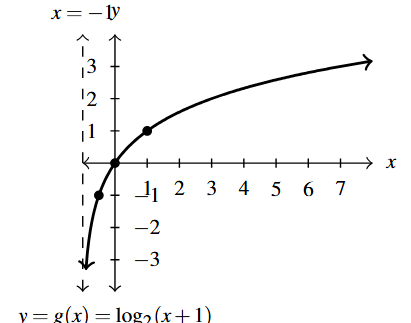
Answer to Exercise 58 - Domain of [latex]g[/latex]: [latex](-1, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Points: [latex]\left( -\frac{1}{2}, -1 \right)[/latex], [latex](0,0)[/latex], [latex](1,1)[/latex]
- Asymptote: [latex]x = -1[/latex]
-
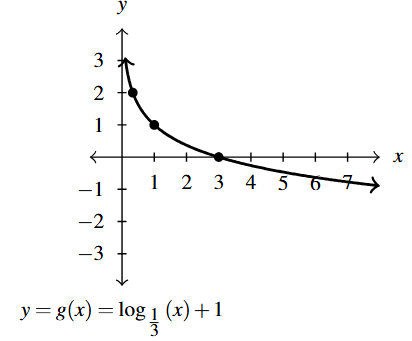
Answer to Exercise 59 - Domain of [latex]g[/latex]: [latex](0, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Points: [latex]\left(\frac{1}{3}, 2 \right)[/latex], [latex](1,1)[/latex], [latex](3,0)[/latex]
- Asymptote: [latex]x = 0[/latex]
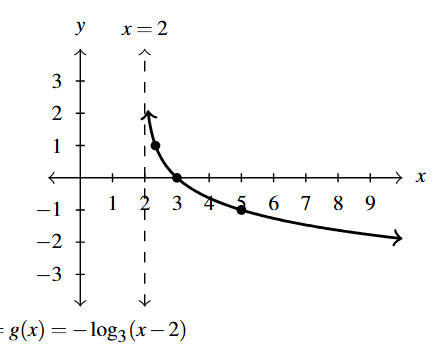
- Domain of [latex]g[/latex]: [latex](2, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Points: [latex]\left( \frac{7}{3},1 \right)[/latex], [latex](3,0)[/latex], [latex](5,-1)[/latex]
- Asymptote: [latex]x = 2[/latex]
-
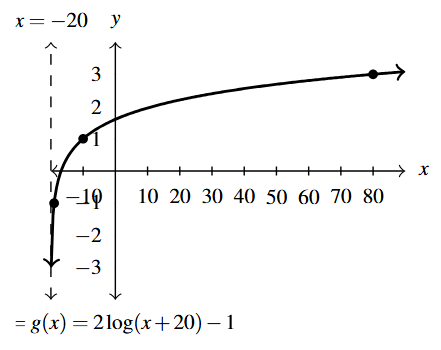
Answer to Exercise 61 - Domain of [latex]g[/latex]: [latex](-20, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Points: [latex](-19, -1)[/latex], [latex](-10,1)[/latex], [latex](80,3)[/latex]
- Asymptote: [latex]x = -20[/latex]
-
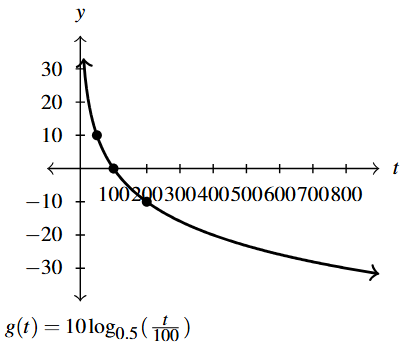
Answer to Exercise 62 - Domain of [latex]g[/latex]: [latex](0, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Points: [latex](50,10)[/latex], [latex](100,0)[/latex], [latex](200,-10)[/latex]
- Asymptote: [latex]t= 0[/latex]
-
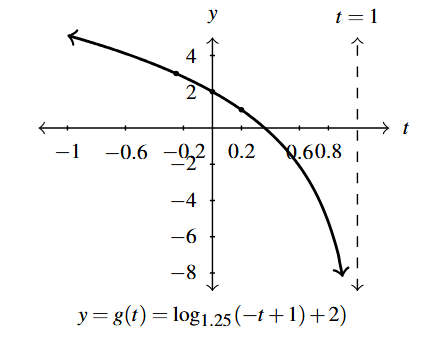
Answer to Exercise 63 - Domain of [latex]g[/latex]: [latex](-\infty, 1)[/latex]
- Range of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Points: [latex](-0.25,3)[/latex], [latex](0,2)[/latex], [latex](0.2,1)[/latex]
- Asymptote: [latex]t = 1[/latex]
-
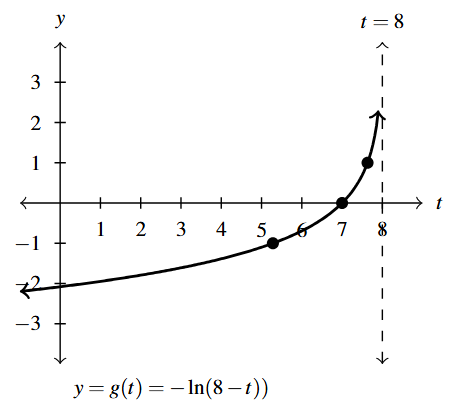
Answer to Exercise 64 - Domain of [latex]g[/latex]: [latex](-\infty, 8)[/latex]
- Range of [latex]g[/latex]:[latex](-\infty, \infty)[/latex]
- Points: [latex](8-e, -1) \approx (5.28, -1)[/latex],
- [latex](7,0)[/latex], [latex](8 - e^{-1}, 1) \approx (7.63,1)[/latex]
- Asymptote: [latex]t = 8[/latex]
-
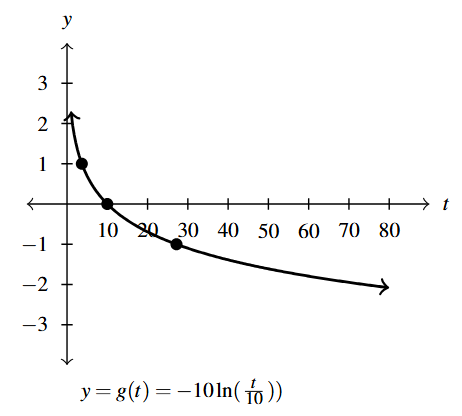
Answer to Exercise 65 - Domain of [latex]g[/latex]: [latex](0, \infty)[/latex]
- Range of [latex]g[/latex]: [latex](-\infty, \infty)[/latex]
- Points: [latex](10e^{-1}, 10) \approx (3.68. 10)[/latex]
- [latex](10,0)[/latex], [latex](10e, -10) \approx (27.18, -10)[/latex]
- Asymptote: [latex]t = 0[/latex]
- [latex]F(x) = \log_{2}(x+3) - 1[/latex]
- [latex]F(x) = -\log_{2}(-x+3)[/latex]
- [latex]F(x) = \frac{1}{2} \log_{2}(x) + 3[/latex]
- [latex]F(x) = -\frac{1}{2} \log_{2} \left( \frac{x}{3} \right)[/latex]
- In order, the formulas for [latex]G(x)[/latex] are:
- [latex]G(x) = 2\log_{4}(x+3) - 1[/latex]
- [latex]G(x) = -2\log_{4}(-x+3)[/latex]
- [latex]G(x) = \log_{4}(x) + 3[/latex]
- [latex]G(x) = - \log_{4} \left( \frac{x}{3} \right)[/latex]
- [latex]y = f(x) = 3^{x + 2} - 4[/latex] (in red), [latex]y = f^{-1}(x) = \log_{3}(x + 4) - 2[/latex] (in blue)
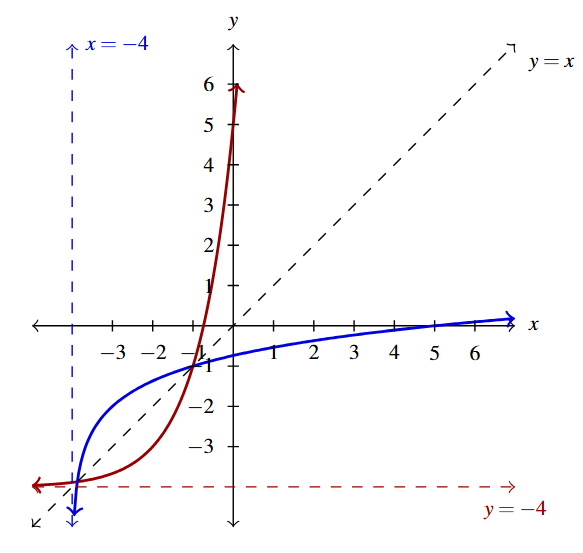
Answer to Exercise 71 - [latex]y = f(x) = \log_{4}(x - 1)[/latex] (in red), [latex]y = f^{-1}(x) = 4^{x} + 1[/latex]
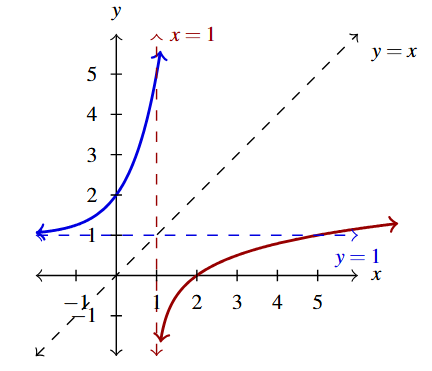
Answer to Exercise 72 - [latex]y = g(t) = -2^{-t} + 1[/latex] (in red), [latex]y = g^{-1}(t) = -\log_{2}(-t+1)[/latex] (in blue)
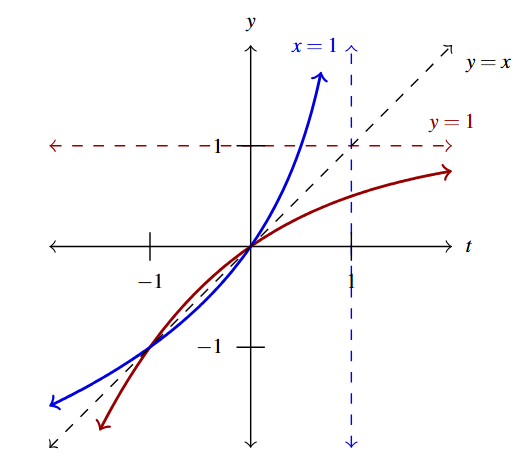
Answer to Exercise 73 - [latex]y = g(t) = 5\log(t) - 2[/latex] (in red), [latex]y = g^{-1}(t) = 10^{\frac{t + 2}{5}}[/latex] (in blue)
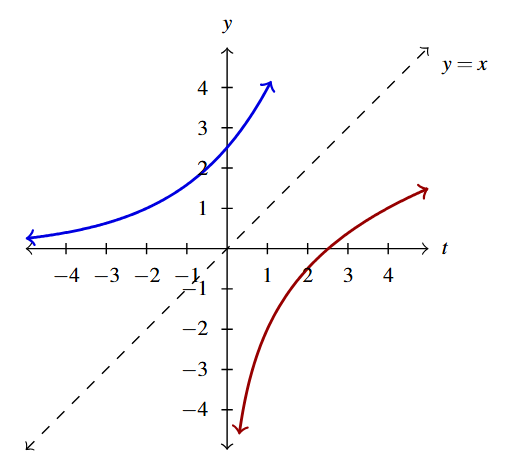
Answer to Exercise 74 - One solution is [latex]g(x) = \log_{2}(x+3)[/latex] and [latex]h(x) = 4[/latex].
- One solution is [latex]g(x) = \log(2x)[/latex] and [latex]h(x) = e^{-x}[/latex].
- One solution is [latex]g(t) = 3t[/latex] and [latex]h(t) = \log(t)[/latex].
- One solution is [latex]f(x) = \ln(x)[/latex] and [latex]g(x)=x[/latex].
- One solution is [latex]f(t) = t^2+1[/latex] and [latex]g(t) = \ln(t)[/latex].
- One solution is [latex]f(z) = \ln(z)[/latex] and [latex]g(z) = z^2[/latex].
- .
- [latex]M(0.001) = \log \left(\frac{0.001}{0.001} \right) = \log(1) = 0[/latex].
- [latex]M(80,000) = \log \left(\frac{80,000}{0.001} \right) = \log(80,000,000) \approx 7.9[/latex]
- .
- [latex]L(10^{-6}) = 60[/latex] decibels.
- [latex]I = 10^{-.5} \approx 0.316[/latex] watts per square meter.
- Because [latex]L(1) = 120[/latex] decibels and [latex]L(100) = 140[/latex] decibels, a sound with intensity level 140 decibels has an intensity 100 times greater than a sound with intensity level 120 decibels.
- .
- The pH of pure water is 7.
- If [latex][\mbox{H}^{+}] = 6.3 \times 10^{-13}[/latex] then the solution has a pH of 12.2.
- [latex][\mbox{H}^{+}] = 10^{-0.7} \approx .1995[/latex] moles per liter.
Section 5.4 answers
- [latex]3\ln(x) + 2\ln(y)[/latex]
- [latex]7 - \log_{2}(x^{2} + 4)[/latex]
- [latex]3\log_{5}(z) - 6[/latex]
- [latex]\log(1.23) + 37[/latex]
- [latex]\frac{1}{2}\ln(z) - \ln(x) - \ln(y)[/latex]
- [latex]\log_{5}(x-5) + \log_{5}(x+5)[/latex]
- [latex]3\log_{\sqrt{2}}(x) + 4[/latex]
- [latex]-2 + \log_{\frac{1}{3}}(x) + \log_{\frac{1}{3}}(y - 2) + \log_{\frac{1}{3}}(y^{2} + 2y + 4)[/latex]
- [latex]3 + 3\log(x) + 5 \log(y)[/latex]
- [latex]2\log_{3}(x) - 4 - 4\log_{3}(y)[/latex]
- [latex]\frac{1}{4} \ln(x) + \frac{1}{4} \ln(y) - \frac{1}{4} - \frac{1}{4} \ln(z)[/latex]
- [latex]12-12\log_{6}(x) - 4\log_{6}(y)[/latex]
- [latex]\frac{5}{3}+\log(x)+\frac{1}{2}\log(y)[/latex]
- [latex]-2+\frac{2}{3}\log_{\frac{1}{2}}(x)-\log_{\frac{1}{2}}(y)-\frac{1}{2}\log_{\frac{1}{2}}(z)[/latex]
- [latex]\frac{1}{3} \ln(x) - \ln(10) - \frac{1}{2}\ln(y)-\frac{1}{2}\ln(z)[/latex]
- [latex]\ln(x^{4}y^{2})[/latex]
- [latex]\log_{2}\left(\frac{xy}{z}\right)[/latex]
- [latex]\log_{3} \left( \frac{x}{y^2} \right)[/latex]
- [latex]\log_{3} \left( \frac{x}{y^2} \right)[/latex]
- [latex]\ln\left( \frac{x^2}{y^3z^4} \right)[/latex]
- [latex]\log\left(\frac{x \sqrt{y}}{\sqrt[3]{z}} \right)[/latex]
- [latex]\ln\left(\sqrt[3]{\frac{z}{xy}} \right)[/latex]
- [latex]\log_{5}\left(\frac{x}{125}\right)[/latex]
- [latex]\log\left(\frac{1000}{x}\right)[/latex]
- [latex]\log_{7}\left(\frac{x(x - 3)}{49}\right)[/latex]
- [latex]\ln \left(x \sqrt{e} \right)[/latex]
- [latex]\log_{2}\left(x^{3/2}\right)[/latex]
- [latex]\log_{2}\left(x \sqrt{x-1}\right)[/latex]
- [latex]\log_{2}\left(\frac{x}{x - 1}\right)[/latex]
- [latex]7^{x - 1} = e^{(x - 1)\ln(7)}[/latex]
- [latex]\log_{3}(x + 2) = \frac{\log(x + 2)}{\log(3)}[/latex]
- [latex]\left(\frac{2}{3}\right)^{x} = e^{x\ln(\frac{2}{3})}[/latex]
- [latex]\log(x^{2} + 1) = \frac{\ln(x^{2} + 1)}{\ln(10)}[/latex]
- [latex]\log_{3}(12) \approx 2.26186[/latex]
- [latex]\log_{5}(80) \approx 2.72271[/latex]
- [latex]\log_{6}(72) \approx 2.38685[/latex]
- [latex]\log_{4}\left(\frac{1}{10}\right) \approx -1.66096[/latex]
- [latex]\log_{\frac{3}{5}}(1000) \approx -13.52273[/latex]
- [latex]\log_{\frac{2}{3}}(50) \approx -9.64824[/latex]
Section 5.5 Answers
- [latex]x = \frac{3}{4}[/latex]
- [latex]x = 4[/latex]
- [latex]x=2[/latex]
- [latex]t = -\frac{1}{4}[/latex]
- [latex]t = -\frac{7}{3}[/latex]
- [latex]t = -1, \, 0, \, 1[/latex]
- [latex]x = \frac{16}{15}[/latex]
- [latex]x=-\frac{2}{11}[/latex]
- [latex]x = \dfrac{\ln(5)}{2\ln(3)}[/latex]
- [latex]t = -\dfrac{\ln(2)}{\ln(5)}[/latex]
- No solution.
- [latex]t = \dfrac{\ln(29) + \ln(3)}{\ln(3)}[/latex]
- [latex]x = \dfrac{\ln(3)}{12\ln(1.005)}[/latex]
- [latex]k = \dfrac{\ln\left(\frac{1}{2}\right)}{-5730} = \dfrac{\ln(2)}{5730}[/latex]
- [latex]t=\dfrac{\ln(2)}{0.1} = 10\ln(2)[/latex]
- [latex]t=\frac{1}{2}\ln\left(\frac{1}{2}\right) = -\frac{1}{2}\ln(2)[/latex]
- [latex]t = \dfrac{\ln\left(\frac{1}{18}\right)}{-0.1} =10 \ln(18)[/latex]
- [latex]t=-10\ln\left(\frac{5}{3}\right) = 10\ln\left(\frac{3}{5}\right)[/latex]
- [latex]x=\ln(2)[/latex]
- [latex]t=\frac{1}{3}\ln(2)[/latex]
- [latex]t = \dfrac{\ln\left(\frac{1}{29}\right)}{-0.8} = \dfrac{5}{4}\ln(29)[/latex]
- [latex]x = \dfrac{\ln\left(\frac{2}{5}\right)}{\ln\left(\frac{4}{5}\right)} = \dfrac{\ln(2)-\ln(5)}{\ln(4) - \ln(5)}[/latex]
- [latex]x = \ln(2)[/latex]
- [latex]t = -\frac{1}{8} \ln\left(\frac{1}{4} \right) = \frac{1}{4}\ln(2)[/latex]
- [latex]x = \dfrac{\ln(3)}{\ln(3) - \ln(2)}[/latex]
- [latex]x = \dfrac{\ln(3) + 5\ln\left(\frac{1}{2}\right)}{\ln(3) - \ln\left(\frac{1}{2}\right)} = \dfrac{\ln(3)-5\ln(2)}{\ln(3)+\ln(2)}[/latex]
- [latex]x = \dfrac{4 \ln(3) - 3 \ln(7)}{7 \ln(7) + 2 \ln(3)}[/latex]
- [latex]t=\ln(5)[/latex]
- [latex]t=\ln(3)[/latex]
- [latex]t=\dfrac{\ln(3)}{\ln(2)}[/latex]
- [latex]x=\ln(3)[/latex]
- [latex]x=\ln(3)[/latex], [latex]\ln(5)[/latex]
- [latex]x=\dfrac{\ln(5)}{\ln(3)}[/latex]
- [latex](-\infty, \infty)[/latex]
- [latex](-\infty, 0) \cup (0, \infty)[/latex]
- [latex]\left( \frac{1}{2} \ln(3), \infty \right)[/latex]
- [latex](-\infty, \infty)[/latex]
- [latex](-\infty, \ln(3))[/latex]
- [latex](\ln(2), \infty)[/latex]
- [latex]f^{-1} = \ln\left(x + \sqrt{x^{2} + 1}\right)[/latex]. Both [latex]f[/latex] and [latex]f^{-1}[/latex] have domain [latex](-\infty, \infty)[/latex] and range [latex](-\infty, \infty)[/latex].
Section 5.6 Answers
- [latex]x = \frac{5}{4}[/latex]
- [latex]x = 1[/latex]
- [latex]t=-2[/latex]
- [latex]t=-3,\, 4[/latex]
- [latex]x=-1[/latex]
- [latex]x=\frac{9}{2}[/latex]
- [latex]t=\pm 10[/latex]
- [latex]t=-2,\, 5[/latex]
- [latex]x = -\frac{17}{7}[/latex]
- [latex]x = 10^{1.7}[/latex]
- [latex]x = 10^{-5.4}[/latex]
- [latex]x = 10^{3}[/latex]
- [latex]t=\frac{25}{2}[/latex]
- [latex]t=e^{3/4}[/latex]
- [latex]t = 5[/latex]
- [latex]t = \frac{1}{2}[/latex]
- [latex]x = 2[/latex]
- [latex]x = \frac{1}{e^3-1}[/latex]
- [latex]t=6[/latex]
- [latex]t=4[/latex]
- [latex]x = 81[/latex]
- [latex]x = e^{e^3}[/latex]
- [latex]t=10^{-3}, \, 10^{5}[/latex]
- [latex]t = 1, \, x = e^{2}[/latex]
- [latex](-\infty, e) \cup (e, \infty)[/latex]
- [latex](0,e) \cup (e, \infty)[/latex]
- [latex](0, 100][/latex]
- [latex](0, \infty)[/latex]
- [latex](1, \infty)[/latex]
- [latex](1,e)[/latex]
- [latex]y = \dfrac{3}{5e^{2x} + 1}[/latex]
- Answers May Vary
- [latex]f^{-1}(x) = \dfrac{e^{2x} - 1}{e^{2x} + 1} = \dfrac{e^{x} - e^{-x}}{e^{x} + e^{-x}}[/latex], The domain of [latex]f^{-1}[/latex] is [latex](-\infty, \infty)[/latex] and its range is the same as the domain of [latex]f[/latex], namely [latex](-1, 1)[/latex].
Section 5.7 Answers
- [latex]A(t) = 500\left(1 + \frac{0.0075}{12}\right)^{12t}[/latex]
- [latex]A(5) \approx \$ 519.10[/latex],
- [latex]A(10) \approx \$ 538.93[/latex],
- [latex]A(30) \approx \$ 626.12[/latex],
- [latex]A(35) \approx \$ 650.03[/latex]
- It will take approximately 92 years for the investment to double.
- The average rate of change from the end of the fourth year to the end of the fifth year is approximately 3.88. This means that the investment is growing at an average rate of \$3.88 per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately 4.85. This means that the investment is growing at an average rate of \$4.85 per year at this point.
- [latex]A(t) = 500e^{0.0075t}[/latex]
- [latex]A(5) \approx \$ 519.11[/latex],
- [latex]A(10) \approx \$ 538.94[/latex],
- [latex]A(30) \approx \$ 626.16[/latex],
- [latex]A(35) \approx \$ 650.09[/latex]
- It will take approximately 92 years for the investment to double.
- The average rate of change from the end of the fourth year to the end of the fifth year is approximately 3.88. This means that the investment is growing at an average rate of \$3.88 per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately 4.86. This means that the investment is growing at an average rate of \$4.86 per year at this point.
- [latex]A(t) = 1000\left(1 + \frac{0.0125}{12}\right)^{12t}[/latex]
- [latex]A(5) \approx \$ 1064.46[/latex],
- [latex]A(10) \approx \$ 1133.07[/latex],
- [latex]A(30) \approx \$ 1454.71[/latex],
- [latex]A(35) \approx \$ 1548.48[/latex]
- It will take approximately 55 years for the investment to double.
\item The average rate of change from the end of the fourth year to the end of the fifth year is approximately 13.22. This means that the investment is growing at an average rate of \$13.22 per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately 19.23. This means that the investment is growing at an average rate of \$19.23 per year at this point.
- [latex]A(t) = 1000e^{0.0125t}[/latex]
- [latex]A(5) \approx \$ 1064.49[/latex],
- [latex]A(10) \approx \$ 1133.15[/latex],
- [latex]A(30) \approx \$ 1454.99[/latex],
- [latex]A(35) \approx \$ 1548.83[/latex]
- It will take approximately 55 years for the investment to double.
- The average rate of change from the end of the fourth year to the end of the fifth year is approximately 13.22. This means that the investment is growing at an average rate of \$13.22 per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately 19.24. This means that the investment is growing at an average rate of \$19.24 per year at this point.
- [latex]A(t) = 5000\left(1 + \frac{0.02125}{12}\right)^{12t}[/latex]
- [latex]A(5) \approx \$ 5559.98[/latex],
- [latex]A(10) \approx \$ 6182.67[/latex],
- [latex]A(30) \approx \$ 9453.40[/latex],
- [latex]A(35) \approx \$ 10512.13[/latex]
- It will take approximately 33 years for the investment to double.
- The average rate of change from the end of the fourth year to the end of the fifth year is approximately 116.80. This means that the investment is growing at an average rate of \$116.80 per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately 220.83. This means that the investment is growing at an average rate of \$220.83 per year at this point.
- [latex]A(t) = 5000e^{0.02125t}[/latex]
- [latex]A(5) \approx \$ 5560.50[/latex],
- [latex]A(10) \approx \$ 6183.83[/latex],
- [latex]A(30) \approx \$ 9458.73[/latex],
- [latex]A(35) \approx \$ 10519.05[/latex]
- It will take approximately 33 years for the investment to double.
- The average rate of change from the end of the fourth year to the end of the fifth year is approximately 116.91. This means that the investment is growing at an average rate of \$116.91 per year at this point. The average rate of change from the end of the thirty-fourth year to the end of the thirty-fifth year is approximately 221.17. This means that the investment is growing at an average rate of \$221.17 per year at this point.
- Answers May Vary
- [latex]P = \frac{2000}{e^{0.0025 \cdot 3}} \approx \$ 1985.06[/latex]
- [latex]P = \frac{5000}{\left(1 + \frac{0.0225}{12}\right)^{12 \cdot 10}} \approx \$ 3993.42[/latex]
- .
- [latex]A(8) = 2000\left(1 + \frac{0.0025}{12}\right)^{12 \cdot 8} \approx \$2040.40[/latex]
- [latex]t = \dfrac{\ln(2)}{12 \ln\left(1 + \frac{0.0025}{12}\right)} \approx 277.29[/latex] years
- [latex]P = \dfrac{2000}{\left(1 + \frac{0.0025}{12}\right)^{36}} \approx \$1985.06[/latex]
- .
- [latex]A(8) = 2000\left(1 + \frac{0.0225}{12}\right)^{12 \cdot 8} \approx \$2394.03[/latex]
- [latex]t = \dfrac{\ln(2)}{12 \ln\left(1 + \frac{0.0225}{12}\right)} \approx 30.83[/latex] years
- [latex]P = \dfrac{2000}{\left(1 + \frac{0.0225}{12}\right)^{36}} \approx \$1869.57[/latex]
- [latex]\left(1 + \frac{0.0225}{12}\right)^{12} \approx 1.0227[/latex] so the APY is 2.27\%
- [latex]A(3) = 5000e^{0.299 \cdot 3} \approx \$12,226.18[/latex],
[latex]A(6) = 5000e^{0.299 \cdot 6} \approx \$30,067.29[/latex] - Answers May Vary
- .
- [latex]k = \frac{\ln(1/2)}{5.27} \approx -0.1315[/latex]
- [latex]A(t) = 50e^{-0.1315t}[/latex]
- [latex]t = \frac{\ln(0.1)}{-0.1315} \approx 17.51[/latex] years.
- .
- [latex]k = \frac{\ln(1/2)}{14} \approx -0.0495[/latex]
- [latex]A(t) = 2e^{-0.0495t}[/latex]
- [latex]t = \frac{\ln(0.1)}{-0.0495} \approx 46.52[/latex] days.
- .
- [latex]k = \frac{\ln(1/2)}{27.7} \approx -0.0250[/latex]
- [latex]A(t) = 75e^{-0.0250t}[/latex]
- [latex]t = \frac{\ln(0.1)}{-0.025} \approx 92.10[/latex] days.
- .
- [latex]k = \frac{\ln(1/2)}{432.7} \approx -0.0016[/latex]
- [latex]A(t) = 0.29e^{-0.0016t}[/latex]
- [latex]t = \frac{\ln(0.1)}{-0.0016} \approx 1439.11[/latex] years.
- .
- [latex]k = \frac{\ln(1/2)}{704} \approx -0.0010[/latex]
- [latex]A(t) = e^{-0.0010t}[/latex]
- [latex]t = \frac{\ln(0.1)}{-0.0010} \approx 2302.58[/latex] million years, or 2.30 billion years.
- [latex]t = \frac{\ln(0.1)}{k} = -\frac{\ln(10)}{k}[/latex]
- [latex]V(t) = 25e^{\ln\left(\frac{4}{5}\right)t} \approx 25e^{-0.22314355t}[/latex]
- .
- [latex]G(0) = 9743.77[/latex] This means that the GDP of the US in 2000 was \$9743.77 billion dollars.
- [latex]G(7) = 13963.24[/latex] and [latex]G(10) = 16291.25[/latex], so the model predicted a GDP of \$ 13,963.24 billion in 2007 and \$ 16,291.25 billion in 2010.
- .
- [latex]D(0) = 15[/latex], so the tumor was 15 millimeters in diameter when it was first detected.
- [latex]t = \frac{\ln(2)}{0.0277} \approx 25[/latex] days.
- .
- [latex]k = \frac{\ln(2)}{20} \approx 0.0346[/latex]
- [latex]N(t) = 1000e^{0.0346 t}[/latex]
- [latex]t = \frac{\ln(9)}{0.0346} \approx 63[/latex] minutes
- .
- [latex]k = \frac{1}{2}\frac{\ln(6)}{2.5} \approx 0.4377[/latex]
- [latex]N(t) = 2.5e^{0.4377 t}[/latex]
- [latex]t = \frac{\ln(2)}{0.4377} \approx 1.58[/latex] hours
- [latex]N_{0} = 52[/latex], [latex]k = \frac{1}{3} \ln\left( \frac{118}{52}\right) \approx 0.2731[/latex], [latex]N(t) = 52e^{0.2731t}[/latex]
- [latex]N_{0} = 2649[/latex], [latex]k = \frac{1}{60} \ln\left( \frac{7272}{2649}\right) \approx 0.0168[/latex], [latex]N(t) = 2649e^{0.0168t}[/latex]. [latex]N(150) \approx 32923[/latex], so the population of Painesville in 2010 based on this model would have been 32,923.
- .
- [latex]P(0) = \frac{120}{4.167} \approx 29[/latex]. There are 29 Sasquatch in Bigfoot County in 2010.
- [latex]P(3) = \frac{120}{1+3.167e^{-0.05(3)}} \approx 32[/latex] Sasquatch.
- [latex]t = 20 \ln(3.167) \approx 23[/latex] years.
- As [latex]t \rightarrow \infty[/latex], [latex]P(t) \rightarrow 120[/latex]. As time goes by, the Sasquatch Population in Bigfoot County will approach 120. Graphically, [latex]y = P(x)[/latex] has a horizontal asymptote [latex]y=120[/latex].
- b. The average rates of change are listed in order below. They suggest slope at [latex](1,5)[/latex] is 2.5.
- [latex]\approx 2.487[/latex]
- [latex]\approx 2.498[/latex]
- [latex]\approx 2.500[/latex]
- [latex]\approx 2.500[/latex]
- [latex]\approx 2.498[/latex]
- [latex]\approx 2.487[/latex]
- .
- [latex]A(t) = Ne^{-\left(\frac{\ln(2)}{5730}\right)t} \approx Ne^{-0.00012097t}[/latex]
- [latex]A(20000) \approx 0.088978 \cdot N[/latex] so about 8.9\% remains
- [latex]t \approx \dfrac{\ln(.42)}{-0.00012097} \approx 7171[/latex] years old
- [latex]A(t) = 2.3e^{-0.0138629t}[/latex]
- Answer May Vary
- .
- [latex]T(t) = 75 + 105e^{-0.005005t}[/latex]
- The roast would have cooled to [latex]140^{\circ}[/latex]F in about 95 minutes.
- From the graph, it appears that as [latex]x \rightarrow 0^{+}[/latex], [latex]y \rightarrow \infty[/latex]. This is due to the presence of the [latex]\ln(x)[/latex] term in the function. This means that Fritzy will never catch Chewbacca, which makes sense as Chewbacca has a head start and Fritzy only runs as fast as he does.
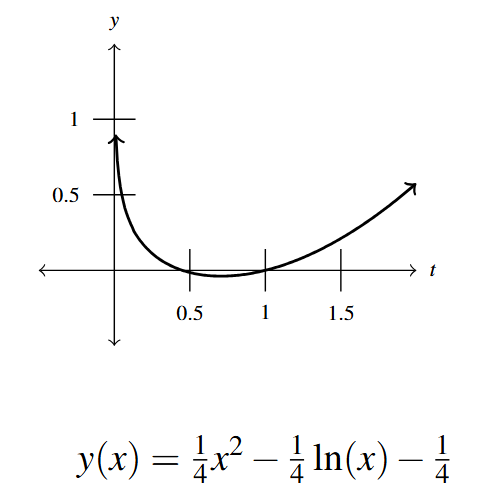
Graphical Answer to Exercise 33 - The steady state current is 2 amps.
- Answers May Vary
- 630 feet.

