"

Section 1.1 Answers

  1. The required points [latex]A(-3, -7), \; B(1.3, -2), \; C(\pi, \sqrt{10}), \; D(0, 8), \; E(-5.5, 0), \; F(-8, 4), \; G(9.2, -7.8)[/latex], and [latex]H(7, 5)[/latex] are plotted in the Cartesian Coordinate Plane below.
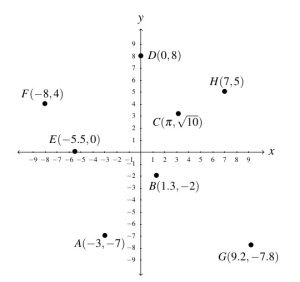
    The cartesian coordinate plane with points C and H plotted in the first quadrant. Point D is on the positive y-axis. Point F is in the second quadrant. Point E is on the negative x-axis. Point A is in the third quadrant and points B and G are in the fourth quadrant.
    Answer to Exercise 1
  2. Points
    1. The point [latex]A(-3, -7)[/latex] is
      • in Quadrant III
      • symmetric about the [latex]x[/latex]-axis with [latex](-3,7)[/latex]
      • symmetric about [latex]y[/latex]-axis with [latex](3, -7)[/latex]
      • symmetric about origin with [latex](3, 7)[/latex]
    2. The point [latex]B(1.3, -2)[/latex] is
      • in Quadrant IV
      • symmetric about [latex]x[/latex]-axis with [latex](1.3, 2)[/latex]
      • symmetric about [latex]y[/latex]-axis with [latex](-1.3, -2)[/latex]
      • symmetric about origin with [latex](-1.3, 2)[/latex]
    3. The point [latex]C(\pi, \sqrt{10})[/latex] is
      • in Quadrant I
      • symmetric about [latex]x[/latex]-axis with [latex](\pi, -\sqrt{10})[/latex]
      • symmetric about [latex]y[/latex]-axis with [latex](-\pi, \sqrt{10})[/latex]
      • symmetric about origin with [latex](-\pi, -\sqrt{10})[/latex]
    4. The point [latex]D(0, 8)[/latex] is
      • on the positive [latex]y[/latex]-axis
      •  symmetric about [latex]x[/latex]-axis with [latex](0, -8)[/latex]
      • symmetric about [latex]y[/latex]-axis with [latex](0, 8)[/latex]
      • symmetric about origin with [latex](0, -8)[/latex]
    5. The point [latex]E(-5.5, 0)[/latex] is
      • on the negative [latex]x[/latex]-axis
      • symmetric about [latex]x[/latex]-axis with [latex](-5.5, 0)[/latex]
      • symmetric about [latex]y[/latex]-axis with [latex](5.5, 0)[/latex]
      • symmetric about origin with [latex](5.5, 0)[/latex]
    6. The point [latex]F(-8, 4)[/latex] is
      • in Quadrant II
      • symmetric about [latex]x[/latex]-axis with [latex](-8, -4)[/latex]
      • symmetric about [latex]y[/latex]-axis with [latex](8, 4)[/latex]
      • symmetric about origin with [latex](8, -4)[/latex]
    7. The point [latex]G(9.2, -7.8)[/latex] is
      • in Quadrant IV
      • symmetric about [latex]x[/latex]-axis with [latex](9.2, 7.8)[/latex]
      • symmetric about [latex]y[/latex]-axis with [latex](-9.2, -7.8)[/latex]
      • symmetric about origin with [latex](-9.2, 7.8)[/latex]
    8. The point [latex]H(7, 5)[/latex] is
      • in Quadrant I
      • symmetric about [latex]x[/latex]-axis with [latex](7, -5)[/latex]
      • symmetric about [latex]y[/latex]-axis with [latex](-7, 5)[/latex]
      • symmetric about origin with [latex](-7, -5)[/latex]
  3. [latex]d = 5[/latex] units, [latex]M = \left(-1, \frac{7}{2} \right)[/latex]
  4. [latex]d = 4 \sqrt{10}[/latex]units, [latex]M = \left(1, -4 \right)[/latex]
  5. [latex]d = \sqrt{26}[/latex] units, [latex]M = \left(1, \frac{3}{2} \right)[/latex]
  6. [latex]d= \frac{\sqrt{37}}{2}[/latex] units, [latex]M = \left(\frac{5}{6}, \frac{7}{4} \right)[/latex]
  7. [latex]d = \sqrt{74}[/latex] units, [latex]M = \left(\frac{13}{10}, -\frac{13}{10} \right)[/latex]
  8. [latex]d= 3\sqrt{5}[/latex] units, [latex]M = \left(-\frac{\sqrt{2}}{2}, -\frac{\sqrt{3}}{2} \right)[/latex]
  9. [latex]d = \sqrt{83}[/latex] units, [latex]M = \left(4 \sqrt{5}, \frac{5 \sqrt{3}}{2} \right)[/latex]
  10. [latex]d = 2[/latex] units, [latex]M = \left( 0, 0\right)[/latex]
  11. [latex](-3, -4)[/latex], 5 miles, [latex](4, -4)[/latex]
  12. The distance from [latex]A[/latex] to [latex]B[/latex] is [latex]|AB| = \sqrt{13},[/latex]the distance from [latex]A[/latex] to [latex]C[/latex] is [latex]|AC| = \sqrt{52},[/latex] and the distance from [latex]B[/latex] to [latex]C[/latex] is [latex]|BC| = \sqrt{65}.[/latex] because [latex]\left(\sqrt{13}\right)^2 + \left( \sqrt{52} \right)^2 = \left( \sqrt{65} \right)^2,[/latex] we are guaranteed by the converse of the Pythagorean Theorem that the triangle is a right triangle.

Section 1.2 Answers

  1. The mapping [latex]M[/latex] is not a function because “Tennant” is matched with both “Eleven” and “Twelve.”
  2. The mapping [latex]C[/latex] is a function because each input is matched with only one output. The domain of [latex]C[/latex] is [latex]\{[/latex] Hartnell, Cushing, Hurndall, Troughton [latex]\}[/latex] and the range is [latex]\{[/latex] One, Two [latex]\}[/latex]. We can represent [latex]C[/latex] as the following set of ordered pairs: [latex]\{ (\text{Hartnell}, \text{One}), (\text{Cushing}, \text{One}), (\text{Hurndall}, \text{One}), (\text{Troughton}, \text{Two}) \}[/latex]
  3. In this case, [latex]y[/latex] is a function of [latex]x[/latex] because each [latex]x[/latex] is matched with only one [latex]y[/latex].The domain is [latex]\{ -3, -2, -1,0,1,2,3 \}[/latex] and the range is [latex]\{ 0,1,2,3 \}[/latex].As ordered pairs, this function is [latex]\{ (-3,3), (-2,2), (-1,1), (0,0), (1,1), (2,2), (3,3) \}[/latex]
  4. In this case, [latex]y[/latex] is not a function of [latex]x[/latex] because there are [latex]x[/latex] values matched with more than one [latex]y[/latex] value. For instance, 1 is matched both to 1 and [latex]-1[/latex].
  5. The mapping is a function because given any word, there is only one answer to “how many letters are in the word?” For the range, we would need to know what the length of the longest word is and whether or not we could find words of all the lengths between 1 (the length of the word “a”) and it.
  6. Because Grover Cleveland was both the 22nd and 24th POTUS, neither mapping described in this exercise is a function.
  7. The outdoor temperature could never be the same for more than two different times – so, for example, it could always be getting warmer or it could always be getting colder.
  8. [latex]f(2) = \frac{7}{4}[/latex], [latex]f(x) = \frac{2x+3}{4}[/latex]
  9. [latex]f(2) = \frac{5}{2}[/latex], [latex]f(x) = \frac{2(x+3)}{4} = \frac{x+3}{2}[/latex]
  10. [latex]f(2) = 7[/latex], [latex]f(x) = 2\left(\frac{x}{4} + 3\right) = \frac{1}{2} x + 6[/latex]
  11. [latex]f(2) = \sqrt{7}[/latex], [latex]f(x) = \sqrt{2x+3}[/latex]
  12. [latex]f(2) = \sqrt{10}[/latex], [latex]f(x) = \sqrt{2(x+3)} = \sqrt{2x+6}[/latex]
  13. [latex]f(2) = 2 \sqrt{5}[/latex], [latex]f(x) = 2\sqrt{x+3}[/latex]
  14. For [latex]f(x) = 2x+1[/latex]
    • [latex]f(3) = 7[/latex]
    • [latex]f(-1) = -1[/latex]
    • [latex]f\left(\frac{3}{2} \right) = 4[/latex]
    • [latex]f(4x) = 8x+1[/latex]
    • [latex]4f(x) = 8x+4[/latex]
    • [latex]f(-x) = -2x+1[/latex]
    • [latex]f(x-4) = 2x-7[/latex]
    • [latex]f(x) - 4 = 2x-3[/latex]
    • [latex]f\left(x^2\right) = 2x^2+1[/latex]
  15. For [latex]f(x) = 3-4x[/latex]
    • [latex]f(3) = -9[/latex]
    • [latex]f(-1) = 7[/latex]
    • [latex]f\left(\frac{3}{2} \right) = -3[/latex]
    • [latex]f(4x) = 3-16x[/latex]
    • [latex]4f(x) = 12-16x[/latex]
    • [latex]f(-x) = 4x+3[/latex]
    • [latex]f(x-4) = 19-4x[/latex]
    • [latex]f(x) - 4 = -4x-1[/latex]
    • [latex]f\left(x^2\right) = 3-4x^2[/latex]
  16. For [latex]f(x) = 2 - x^2[/latex]
    • [latex]f(3) = -7[/latex]
    • [latex]f(-1) = 1[/latex]
    • [latex]f\left(\frac{3}{2} \right) = -\frac{1}{4}[/latex]
    • [latex]f(4x) = 2-16x^2[/latex]
    • [latex]4f(x) = 8-4x^2[/latex]
    • [latex]f(-x) = 2-x^2[/latex]
    • [latex]f(x-4) = -x^2+8x-14[/latex]
    • [latex]f(x) - 4 = -x^{2} - 2[/latex]
  17. For [latex]f(x) = x^2 - 3x + 2[/latex]
    • [latex]f(3) = 2[/latex]
    • [latex]f(-1) = 6[/latex]
    • [latex]f\left(\frac{3}{2} \right) = -\frac{1}{4}[/latex]
    • [latex]f(4x) = 16x^2-12x+2[/latex]
    • [latex]4f(x) = 4x^2-12x+8[/latex]
    • [latex]f(-x) = x^2+3x+2[/latex]
    • [latex]f(x-4) = x^2-11x+30[/latex]
    • [latex]f(x) - 4 = x^2-3x-2[/latex]
    • [latex]f\left(x^2\right) = x^4-3x^2+2[/latex]
  18. For [latex]f(x) = 6[/latex]
    • [latex]f(3) = 6[/latex]
    • [latex]f(-1) =6[/latex]
    • [latex]f\left(\frac{3}{2} \right) = 6[/latex]
    • [latex]f(4x) = 6[/latex]
    • [latex]4f(x) = 24[/latex]
    • [latex]f(-x) = 6[/latex]
    • [latex]f(x-4) = 6[/latex]
    • [latex]f(x) - 4 = 2[/latex]
    • [latex]f\left(x^2\right) = 6[/latex]
  19. For [latex]f(x) = 0[/latex]
    • [latex]f(3) = 0[/latex]
    • [latex]f(-1) =0[/latex]
    • [latex]f\left(\frac{3}{2} \right) = 0[/latex]
    • [latex]f(4x) = 0[/latex]
    • [latex]4f(x) = 0[/latex]
    • [latex]f(-x) = 0[/latex]
    • [latex]f(x-4) = 0[/latex]
    • [latex]f(x) - 4 = -4[/latex]
    • [latex]f\left(x^2\right) = 0[/latex]
  20. For [latex]f(x) = 2x-5[/latex]
    • [latex]f(2) = -1[/latex]
    • [latex]f(-2) = -9[/latex]
    • [latex]f(2a) = 4a-5[/latex]
    • [latex]2 f(a) = 4a-10[/latex]
    • [latex]f(a+2) = 2a-1[/latex]
    • [latex]f(a) + f(2) = 2a-6[/latex]
    • [latex]f \left( \frac{2}{a} \right) = \frac{4}{a} - 5 = \frac{4-5a}{a}[/latex]
    • [latex]\frac{f(a)}{2} =\frac{2a-5}{2}[/latex]
    • [latex]f(a + h) = 2a + 2h - 5[/latex]
  21. For [latex]f(x) = 5-2x[/latex]
    • [latex]f(2) = 1[/latex]
    • [latex]f(-2) = 9[/latex]
    • [latex]f(2a) = 5-4a[/latex]
    • [latex]2 f(a) = 10-4a[/latex]
    • [latex]f(a+2) = 1-2a[/latex]
    • [latex]f(a) + f(2) = 6-2a[/latex]
    • [latex]f \left( \frac{2}{a} \right) = 5 - \frac{4}{a}= \frac{5a-4}{a}[/latex]
    • [latex]\frac{f(a)}{2} = \frac{5-2a}{2}[/latex]
    • [latex]f(a + h) = 5-2a-2h[/latex]
  22. For [latex]f(x) = 2x^2-1[/latex]
    • [latex]f(2) = 7[/latex]
    • [latex]f(-2) = 7[/latex]
    • [latex]f(2a) = 8a^2-1[/latex]
    • [latex]2 f(a) = 4a^2-2[/latex]
    • [latex]f(a+2) = 2a^2+8a+7[/latex]
    • [latex]f(a) + f(2) = 2a^2+6[/latex]
    • [latex]f \left( \frac{2}{a} \right) = \frac{8}{a^2} - 1= \frac{8-a^2}{a^2}[/latex]
    • [latex]\frac{f(a)}{2} = \frac{2a^2-1}{2}[/latex]
    • [latex]f(a + h) = 2a^2+4ah+2h^2-1[/latex]
  23. For [latex]f(x) = 3x^2+3x-2[/latex]
    • [latex]f(2) = 16[/latex]
    • [latex]f(-2) = 4[/latex]
    • [latex]f(2a) = 12a^2+6a-2[/latex]
    • [latex]2 f(a) = 6a^2+6a-4[/latex]
    • [latex]f(a+2) = 3a^2+15a+16[/latex]
    • [latex]f(a) + f(2) = 3a^2+3a+14[/latex]
    • [latex]f \left( \frac{2}{a} \right) = \frac{12}{a^2} + \frac{6}{a} - 2 = \frac{12+6a-2a^2}{a^2}[/latex]
    • [latex]\frac{f(a)}{2} = \frac{3a^2+3a-2}{2}[/latex]
    • [latex]f(a + h) = 3a^2 + 6ah + 3h^2+3a+3h-2[/latex]
  24. For [latex]f(x) = 117[/latex]
    • [latex]f(2) = 117[/latex]
    • [latex]f(-2) = 117[/latex]
    • [latex]f(2a) = 117[/latex]
    • [latex]2 f(a) = 234[/latex]
    • [latex]f(a+2) = 117[/latex]
    • [latex]f(a) + f(2) = 234[/latex]
    • [latex]f \left( \frac{2}{a} \right) = 117[/latex]
    • [latex]\frac{f(a)}{2} = \frac{117}{2}[/latex]
    • [latex]f(a + h) = 117[/latex]
  25. For [latex]f(x) = \frac{x}{2}[/latex]
    • [latex]f(2) = 1[/latex]
    • [latex]f(-2) = -1[/latex]
    • [latex]f(2a) = a[/latex]
    • [latex]2 f(a) = a[/latex]
    • [latex]f(a+2) = \frac{a+2}{2}[/latex]
    • [latex]f(a) + f(2) = \frac{a}{2}+ 1 = \frac{a+2}{2}[/latex]
    • [latex]f \left( \frac{2}{a} \right) = \frac{1}{a}[/latex]
    • [latex]\frac{f(a)}{2} = \frac{a}{4}[/latex]
    • [latex]f(a + h) = \frac{a+h}{2}[/latex]
  26. For [latex]f(x) = 3 - \frac{2}{5} x[/latex], [latex]f(0) = 3[/latex] and [latex]f(x) = 0[/latex] when [latex]x = \frac{15}{2}[/latex]
  27. For [latex]f(x) = 2x^2-6[/latex], [latex]f(0) = -6[/latex] and [latex]f(x) = 0[/latex] when [latex]x = \pm \sqrt{3}[/latex]
  28. For [latex]f(x) = x^2-x-12[/latex], [latex]f(0) = -12[/latex] and [latex]f(x) = 0[/latex] when [latex]x = -3 \text{ or } x=4[/latex]
  29. Function
  30. Function
  31. Function
  32. Not a function
  33. Function
  34. Not a function
  35. Not a function
  36. Function
  37. Not a function
  38. Function
  39. Not a function
  40. Function
  41. Function
  42. Function
  43. Not a function
  44. Function, domain = [latex]\{-3, -2, -1, 0, 1, 2 ,3\}, \; \text{range } = \{0, 1, 4, 9 \}[/latex]
  45. Not a function
  46. Function, domain = [latex]\left\{ -7, -3, 3, 4, 5, 6 \right\}[/latex], range = [latex]\left\{ 0,4,5,6,9 \right\}[/latex]
  47. Function, domain = [latex]\left\{ 1, 4, 9, 16, 25, 36, \ldots \right\} \\ = \left\{ x \, | \, x \text{ is a perfect square} \right\}[/latex], range = [latex]\left\{ 2, 4, 6, 8, 10, 12, \ldots \right\} \\ = \left\{ y \, | \, y \text{  is a positive even integer} \right\}[/latex]
  48. Not a function
  49. Function, domain [latex]= \{x \, | \, x \text{  is irrational} \}[/latex], range [latex]= \{ 1\}[/latex]
  50. Function, domain [latex]= \{x \, | \, 1, 2, 4, 8, \ldots \} = \{x \, | \, x=2^{n}  \text{ for some whole number } n \}[/latex], range [latex]= \{ 0, 1, 2, 3, \ldots \} = \{y \, | \, y \text{ is any whole number}\}[/latex]
  51. Function, domain [latex]= \{x \, | \, x \text{ is any integer} \}[/latex], range [latex]= \{y \, | \, y \text{ is the square of an integer}\}[/latex]
  52. Not a function
  53. Function, domain [latex]= \{x \, | \, -2 \leq x 4 \} = [-2, 4)[/latex],  range = [latex]\{3\}[/latex]
  54. Function, domain [latex]= \{x \, | \, x \text{  is a real number} \} = (-\infty, \infty)[/latex], range [latex]= \{y \, | \, y \geq 0 \} = [0,\infty)[/latex]
  55. Not a function
  56. Horizontal Line Test: A graph on the [latex]xy[/latex]-plane represents [latex]x[/latex] as a function of [latex]y[/latex] if and only if no horizontal line intersects the graph more than once.
  57. Function, domain = [latex]\{-4, -3, -2, -1, 0, 1\}[/latex],  range = [latex]\{-1, 0, 1, 2, 3, 4\}[/latex]
  58. Not a function
  59. Function, domain = [latex](-\infty, \infty)[/latex], range = [latex][1, \infty)[/latex]
  60. Not a function
  61. .
    • Number 58 represents [latex]x[/latex] as a function of [latex]y[/latex], domain = [latex]\{-1, 0, 1, 2, 3, 4\}[/latex] and range = [latex]\{-4, -3, -2, -1, 0, 1 \}[/latex]
    • Number 61 represents [latex]x[/latex] as a function of [latex]y[/latex], domain = [latex](-\infty, \infty)[/latex] and range = [latex][1, \infty)[/latex]
  62. Function, domain = [latex][2, \infty)[/latex], range = [latex][0, \infty)[/latex]
  63. Function, domain = [latex](-\infty, \infty)[/latex],  range = [latex](0, 4][/latex]
  64. Not a function
  65. Function, domain = [latex][-5,-3) \cup(-3, 3)[/latex], range = [latex](-2, -1) \cup [0, 4)[/latex]
  66. Only number 63 represents [latex]v[/latex] as a function of [latex]w[/latex]; domain = [latex][0, \infty)[/latex] and range = [latex][2, \infty)[/latex]
  67. Function, domain = [latex][-2, \infty)[/latex], range = [latex][-3, \infty)[/latex]
  68. Not a function
  69. Function, domain = [latex](-5, 4)[/latex], range = [latex](-4, 4)[/latex]
  70. Function , domain = [latex][0,3) \cup (3,6][/latex], range = [latex](-4,-1] \cup [0,4][/latex]
  71. None of numbers 68 – 71 represent [latex]t[/latex] as a function of [latex]T[/latex].
  72. Function, domain = [latex](-\infty, \infty)[/latex], range = [latex](-\infty, 4][/latex]
  73. Function, domain = [latex](-\infty, \infty)[/latex], range = [latex](-\infty, 4][/latex]
  74. Function, domain = [latex][-2, \infty)[/latex], range = [latex](-\infty, 3][/latex]
  75. Function, domain = [latex](-\infty, \infty)[/latex], range = [latex](-\infty, \infty)[/latex]
  76. Only number 75 represents [latex]s[/latex] as a function of [latex]H[/latex]; domain = [latex](-\infty, 3][/latex] and range = [latex][-2, \infty)[/latex]
  77. Function, domain = [latex](-\infty, 0] \cup (1, \infty)[/latex], range = [latex](-\infty, 1] \cup \{ 2\}[/latex]
  78. Function,  domain = [latex][-3,3][/latex], range = [latex][-2,2][/latex]
  79. Not a function
  80. Function, domain = [latex](-\infty, \infty)[/latex], range = [latex]\{2\}[/latex]
  81. Only number 80 represents [latex]t[/latex] as a function of [latex]u[/latex]; domain = [latex](-\infty, \infty)[/latex] and range=[latex]\{2 \}[/latex]
  82. [latex]f(-2) = 2[/latex]
  83. [latex]g(-2) = -5[/latex]
  84. [latex]f(2) = 3[/latex]
  85. [latex]g(2) = 3[/latex]
  86. [latex]f(0) = -1[/latex]
  87. [latex]g(0) = 0[/latex]
  88. [latex]x = -4, -1, 1[/latex]
  89. [latex]t = -4, 0, 4[/latex]
  90. Domain: [latex][-5,3][/latex], Range: [latex][-5,4][/latex]
  91. Domain: [latex][-4,4][/latex], Range: [latex][-5,5)[/latex]
  92. [latex]f(x) =2-x[/latex], Domain: [latex](-\infty, \infty)[/latex], Range: [latex](-\infty, \infty)[/latex]
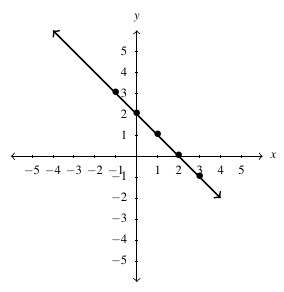
    The line f(x) on the cartesian plane. The line decreases left to right and has a horizontal intercept at x = 2 and a vertical intercept at y = 2.
    Answer to Exercise 93
  93. [latex]g(t) = \dfrac{t - 2}{3}[/latex], Domain: [latex](-\infty, \infty)[/latex], Range: [latex](-\infty, \infty)[/latex]
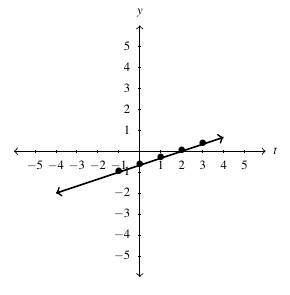
    The line g(t) on the cartesian plane. The line increases left to right and intersects the vertical axis at y = -2/3 and intersects the horizontal axis at x=2.
    Answer to Exercise 94
  94. [latex]h(s) = s^2+1[/latex], Domain: [latex](-\infty, \infty)[/latex], Range: [latex][1, \infty)[/latex]
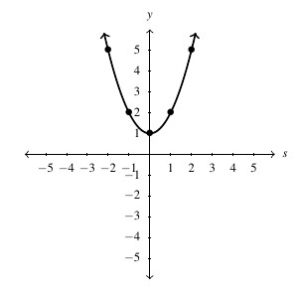
    The curve h(s) on the cartesian plane. The graph is a parabola that opens up. The vertex of the parabola is at (0,1).
    Answer to Exercise 95
  95. [latex]f(x) = 4-x^2[/latex], Domain: [latex](-\infty, \infty)[/latex], Range: [latex](-\infty, 4][/latex]
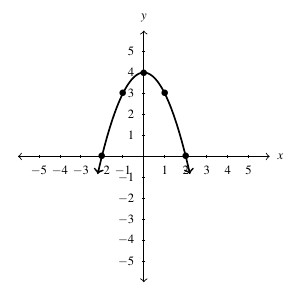
    The curve f(x) on the cartesian plane. The curve is a parabola that opens downward. The vertex of the parabola is at (0,4).
    Answer to Exercise 96
  96. [latex]g(t) = 2[/latex], Domain: [latex](-\infty, \infty)[/latex], Range: [latex]\{2\}[/latex]
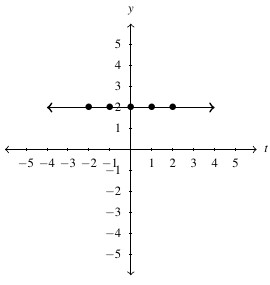
    The line g(t) on the cartesian plane. The line is a horizontal line that intersects the vertical axis at y = 2.
    Answer to Exercise 97
  97. [latex]h(s) = s^3[/latex], Domain: [latex](-\infty, \infty)[/latex], Range: [latex](-\infty, \infty)[/latex]
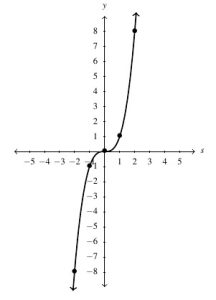
    The curve of h(s) on the cartesian plane. The curve increases from negative infinity to positive infinity and intersects both axes at the origin.
    Answer to Exercise 98
  98. [latex]f(x) = x(x-1)(x+2)[/latex], Domain: [latex](-\infty, \infty)[/latex], Range: [latex](-\infty, \infty)[/latex]
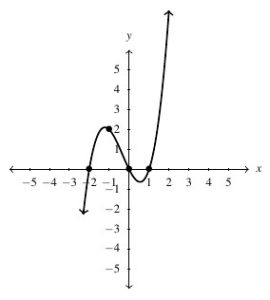
    The curve f(x) on the cartesian plane. The curve intersects the horizontal axis at x = -2, 0, and 1. The graph increases until around x = -1, then decreases until around x = 0.5 and then changes back to increasing.
    Answer to Exercise 99
  99. [latex]g(t) = \sqrt{t-2}[/latex], Domain: [latex][2, \infty)[/latex], Range: [latex][0, \infty)[/latex]
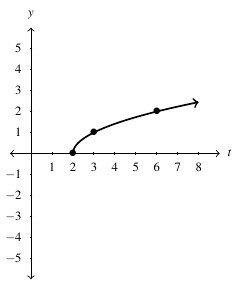
    The curve g(t) on the cartesian plane. The graph starts at the point (2,0) and increases to the right .
    Answer to Exercise 100
  100. [latex]h(s) = \sqrt{5 - s}[/latex], Domain: [latex](-\infty, 5][/latex], Range: [latex][0, \infty)[/latex]
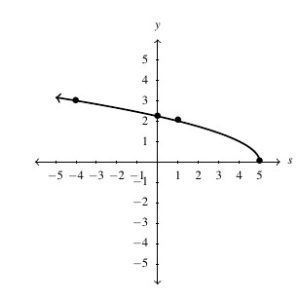
    The curve h(s) on the cartesian plane. The graph decreases from positive infinity to the point (5,0).
    Answer to Exercise 101
  101. [latex]f(x) = 3-2\sqrt{x+2}[/latex], Domain: [latex][-2,\infty)[/latex], Range: [latex](-\infty, 3][/latex]
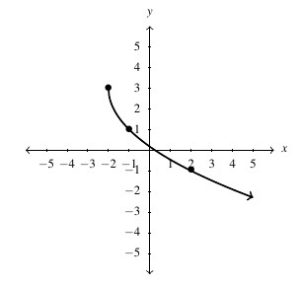
    The curve f(x) on the cartesian plane. The curve starts at (-2,3) and decreases to negative infinity.
    Answer to Exercise 102
  102. [latex]g(t) = \sqrt[3]{t}[/latex], Domain: [latex](-\infty, \infty)[/latex], Range: [latex](-\infty, \infty)[/latex]
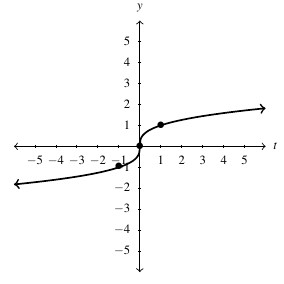
    The curve g(t) on the cartesian plane. The curve increases from left to right, at a very slow rate. The curve intersects both axes at (0,0).
    Answer to Exercise 103
  103. [latex]h(s) = \dfrac{1}{s^{2} + 1}[/latex], Domain: [latex](-\infty, \infty)[/latex], Range: [latex](0, 1][/latex]
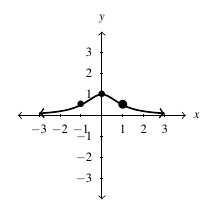
    The curve h(s) on the cartesian plane. The curve remains above the horizontal axis at all times. The graph increases to the point (0,1) and then decreases back towards the horizontal axis.
    Answer to Exercise 104
  104. .
    1. domain [latex]= \{ -1, 0, 1, 2 \}[/latex], range [latex]= \{ -3, 0, 4\}[/latex]
    2. [latex]f(0) = -3[/latex], [latex]f(x) = 0[/latex] for [latex]x = -1, 1[/latex]
    3. [latex]f = \{ (-1,0), (0, -3), (1,0), (2,4) \}[/latex]
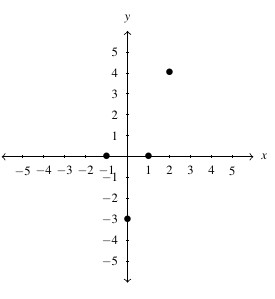
    4. The points (-1,0), (0,-3), (1,0) and (2,4) plotted on the cartesian plane.
      Answer to Exercise 105d
  105. .
    1. domain [latex]= \{ -1, 0, 2, 3 \}[/latex], range [latex]=\{ 2, 3, 4 \}[/latex]
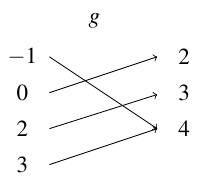
    2. The mapping g. There is a line from -1 in the domain to 4 in the range, 0 from the domain to 2 in the range, from 2 in the domain to 3 in the range, and from 3 in the domain to 4 in the range.
      Answer to Exercise 106b
    3. Find [latex]g(0) = 2[/latex] and [latex]g(x) = 0[/latex] has no solutions.
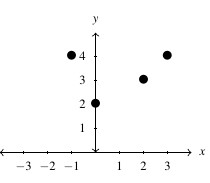
    4. The points (-1,4), (0,2), (2,3), and (3,4) plotted on the cartesian plane.
      Answer to Exercise 106d
  106. [latex]F(4) = 4^2 = 16[/latex] (when [latex]t = 4[/latex]), the solutions to [latex]F(x) = 4[/latex] are [latex]x = \pm 2[/latex] (when [latex]t = \pm 2[/latex]).
  107. [latex]G(4) = 7[/latex] (when [latex]t = 2[/latex]), the solution to [latex]G(t) = 4[/latex] is [latex]x = -2[/latex] (when [latex]t = -1[/latex])
  108. [latex]A(3) = 9[/latex], so the area enclosed by a square with a side of length 3 inches is 9 square inches. The solutions to [latex]A(\ell) = 36[/latex] are [latex]\ell = \pm 6[/latex]. because [latex]\ell[/latex] is restricted to [latex]\ell > 0[/latex], we only keep [latex]\ell = 6[/latex]. This means for the area enclosed by the square to be 36 square inches, the length of the side needs to be 6 inches. because [latex]\ell[/latex] represents a length, [latex]\ell > 0.[/latex]
  109. [latex]A(2) = 4\pi[/latex], so the area enclosed by a circle with radius 2 meters is [latex]4\pi[/latex] square meters. The solutions to [latex]A(r) = 16\pi[/latex] are [latex]r = \pm 4[/latex]. because [latex]r[/latex] is restricted to [latex]r > 0,[/latex] we only keep [latex]r = 4.[/latex] This means for the area enclosed by the circle to be [latex]16\pi[/latex] square meters, the radius needs to be 4 meters. because [latex]r[/latex] represents a radius (length), [latex]r > 0.[/latex]
  110. [latex]V(5) = 125[/latex], so the volume enclosed by a cube with a side of length 5 centimeters is 125 cubic centimeters. The solution to [latex]V(s) = 27[/latex] is [latex]s = 3[/latex]. This means for the volume enclosed by the cube to be [latex]27[/latex] cubic centimeters, the length of the side needs to 3 centimeters. because [latex]x[latex] represents a length, [latex]x > 0[/latex].
  111. [latex]V(3) = 36\pi[/latex], so the volume enclosed by a sphere with radius 3 feet is [latex]36\pi[/latex] cubic feet. The solution to [latex]V(r) = \frac{32\pi}{3}[/latex] is [latex]r = 2[/latex]. This means for the volume enclosed by the sphere to be [latex]\frac{32\pi}{3}[/latex] cubic feet, the radius needs to 2 feet. because [latex]r[latex] represents a radius (length), [latex]r > 0[/latex].
  112. [latex]h(0) = 64[/latex], so at the moment the object is dropped off the building, the object is 64 feet off of the ground. The solutions to [latex]h(t) = 0[/latex] are [latex]t = \pm 2[/latex]. because we restrict [latex]0 \leq t \leq 2[/latex], we only keep [latex]t = 2[/latex]. This means 2 seconds after the object is dropped off the building, it is 0 feet off the ground. Said differently, the object hits the ground after 2 seconds. The restriction [latex]0 \leq t \leq 2[/latex] restricts the time to be between the moment the object is released and the moment it hits the ground.
  113. [latex]T(0) = 3[/latex], so at 6 AM (0 hours after 6 AM), it is [latex]3^{\circ}[/latex] Fahrenheit. [latex]T(6) = 33[/latex], so at noon (6 hours after 6 AM), the temperature is [latex]33^{\circ}[/latex] Fahrenheit. [latex]T(12) = 27[/latex], so at 6 PM (12 hours after 6 AM), it is [latex]27^{\circ}[/latex] Fahrenheit.
  114. [latex]C(0) = 27[/latex], so to make 0 pens, it costs[1] $2700. [latex]C(2) = 11[/latex], so to make 2000 pens, it costs $1100.  [latex]C(5) = 2[/latex], so to make 5000 pens, it costs $2000.
  115. [latex]E(0) = 16.00[/latex], so in 1980 (0 years after 1980), the average fuel economy of passenger cars in the US was 16.00 miles per gallon. [latex]E(14) = 20.81[/latex], so in 1994 (14 years after 1980), the average fuel economy of passenger cars in the US was 20.81 miles per gallon. [latex]E(28) = 22.64[/latex], so in 2008 (28 years after 1980), the average fuel economy of passenger cars in the US was 22.64 miles per gallon.
  116. [latex]P(s) = 4s[/latex], [latex]s > 0[/latex].
  117. [latex]C(D) = \pi D[/latex], [latex]D > 0[/latex].
  118. .
    1. The amount in the retirement account after 30 years if the monthly payment is $50.
    2. The solution to [latex]A(P) = 250000[/latex] is what the monthly payment needs to be in order to have $250,000  in the retirement account after 30 years.
    3. [latex]A(P+50)[/latex] is how much is in the retirement account in 30 years if $50 is added to the monthly payment [latex]P[/latex]. [latex]A(P)+50[/latex] represents the amount of money in the retirement account after 30 years if [latex]P[/latex] dollars is invested each month plus an additional $50. [latex]A(P)+A(50)[/latex] is the sum of money from two retirement accounts after 30 years: one with monthly payment [latex]P[/latex] dollars and one with monthly payment $50.
  119. .
    1. because noon is 4 hours after 8 AM, [latex]P(4)[/latex] gives the chance of precipitation at noon.
    2. We would need to solve [latex]P(t) \geq 50 \%[/latex] or [latex]P(t) \geq 0.5[/latex].
  120. The graph in question passes the horizontal line test meaning for each [latex]w[/latex] there is only one [latex]v.[/latex] The domain of [latex]g[/latex] is [latex][0, \infty)[/latex] (which is the range of [latex]f[/latex]) and the range of [latex]g[/latex] is [latex][2, \infty)[/latex] which is the domain of [latex]f[/latex].
  121. Answers vary.

Section 1.3 Answers

  1. [latex]y+1 = 3(x-3)[/latex] and [latex]y = 3x-10[/latex]
  2. [latex]y-8 = -2(x+5)[/latex]and [latex]y = -2x-2[/latex]
  3. [latex]y + 1 = -(x+7)[/latex] and [latex]y = -x-8[/latex]
  4. [latex]y - 1 = \frac{2}{3} (x+2)[/latex] and [latex]y = \frac{2}{3} x + \frac{7}{3}[/latex]
  5. [latex]y - 4 = -\frac{1}{5} (x-10)[/latex] and [latex]y = -\frac{1}{5} x + 6[/latex]
  6. [latex]y - 4 = \frac{1}{7}(x + 1)[/latex] and [latex]y = \frac{1}{7}x + \frac{29}{7}[/latex]
  7. [latex]y - 117 = 0[/latex] and [latex]y = 117[/latex]
  8. [latex]y + 3 = -\sqrt{2}(x - 0)[/latex] and [latex]y = -\sqrt{2}x - 3[/latex]
  9. [latex]y - 2\sqrt{3} = -5(x - \sqrt{3})[/latex] and [latex]y = -5x + 7\sqrt{3}[/latex]
  10. [latex]y + 12 = 678(x + 1)[/latex] and  [latex]y = 678x + 666[/latex]
  11. [latex]y = -\frac{5}{3}x[/latex]
  12. [latex]y = -2[/latex]
  13. [latex]y = \frac{8}{5}x - 8[/latex]
  14. [latex]y = \frac{9}{4}x - \frac{47}{4}[/latex]
  15. [latex]y = 5[/latex]
  16. [latex]y = -8[/latex]
  17. [latex]y = -\frac{5}{4} x + \frac{11}{8}[/latex]
  18. [latex]y = 2x + \frac{13}{6}[/latex]
  19. [latex]y = -x[/latex]
  20. [latex]y = \frac{\sqrt{3}}{3} x[/latex]
  21. [latex]y =2x-1[/latex], slope: [latex]m = 2[/latex], [latex]y[/latex]-intercept: [latex](0,-1)[/latex], [latex]x[/latex]-intercept: [latex]\left(\frac{1}{2}, 0 \right)[/latex]
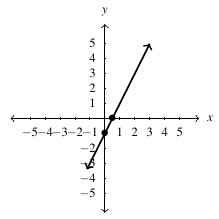
    A line on the cartesian plane. The line intersects the horizontal axis at x=0.5 and the vertical axis at y = -1.
    Answer to Exercise 21
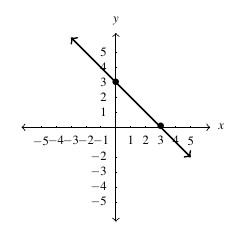
  22. [latex]y =3-x[/latex], slope: [latex]m = -1[/latex], [latex]y[/latex]-intercept: [latex](0,3)[/latex], [latex]x[/latex]-intercept: [latex](3, 0)[/latex]
    A line on the cartesian plane. The line is decreasing left to right. The line intersects the horizontal axis at x=3 and vertical axis at y= 3.
    Answer to Exercise 22
  23. [latex]y = 3[/latex], slope: [latex]m =0[/latex], [latex]y[/latex]-intercept: [latex](0,3)[/latex], [latex]x[/latex]-intercept: none
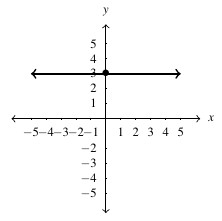
    A line on the cartesian plane the line is horizontal at y = 3.
    Answer to Exercise 23
  24. [latex]y = 0[/latex], slope: [latex]m =0[/latex], [latex]y[/latex]-intercept: [latex](0,0)[/latex], [latex]x[/latex]-intercept: [latex]\{ (x,0) \, | \, x \text{ is a real number} \}[/latex]
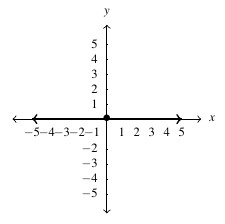
    A horizontal line on the cartesian plane. The line runs along the x-axis.
    Answer to Exercise 24
  25. [latex]y = \frac{2}{3} x + \frac{1}{3}[/latex], slope: [latex]m = \frac{2}{3}[/latex], [latex]y[/latex]-intercept: [latex]\left(0, \frac{1}{3}\right)[/latex], [latex]x[/latex]-intercept: [latex]\left(-\frac{1}{2}, 0\right)[/latex]
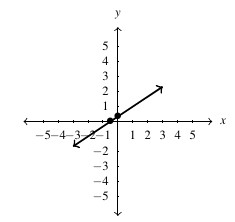
    A line on the cartesian plane. The line increases left to right and intersects the horizontal axis at x=-.5 and the horizontal axis at y = 1/3.
    Answer to Exercise 25
  26. [latex]y = \dfrac{1-x}{2}[/latex], slope: [latex]m = -\frac{1}{2}[/latex], [latex]y[/latex]-intercept: [latex]\left(0, \frac{1}{2}\right)[/latex], [latex]x[/latex]-intercept: [latex]\left(1, 0\right)[/latex]
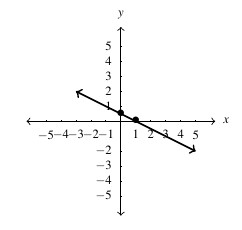
    A line which decreases from left to right. The line intersects the horizontal axis at x = 1 and intersects the vertical axis at y =0.5.
    Answer to Exercise 26
  27. [latex]w = -\frac{3}{2} v + 3[/latex], slope: [latex]m = -\frac{3}{2}[/latex], [latex]w[/latex]-intercept: [latex]\left(0, 3\right)[/latex], [latex]v[/latex]-intercept: [latex]\left(2, 0\right)[/latex]
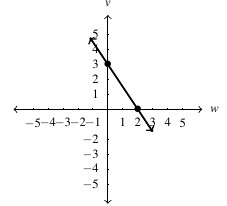
    A line on the cartesian plane. The line is decreasing left to right. The line intersects the vertical axis at y = 3 and intersects the horizontal axis at x = 2.
    Answer to Exercise 27
  28. [latex]v = -\frac{2}{3} w + 2[/latex], slope: [latex]m = -\frac{2}{3}[/latex], [latex]v[/latex]-intercept: [latex]\left(0,2 \right)[/latex], [latex]w[/latex]-intercept: [latex]\left(3,0\right)[/latex]
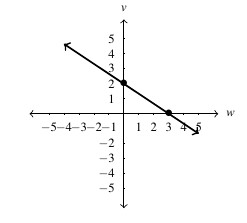
    A line on the cartesian plane. The line is decreasing left to right and intersects the vertical axis at y =2 and the horizontal axis at x = 3.
    Answer to Exercise 28
  29. [latex](-1,-1)[/latex] and [latex]\left(\frac{11}{5}, \frac{27}{5}\right)[/latex]
  30. [latex]y = 3x[/latex]
  31. [latex]y = -6x + 20[/latex]
  32. [latex]y = \frac{2}{3} x - 4[/latex]
  33. [latex]y = -\frac{1}{3} x - \frac{2}{3}[/latex]
  34. [latex]y=-2[/latex]
  35. [latex]x=-5[/latex]
  36. [latex]y = -3x[/latex]
  37. [latex]y = \frac{1}{6}x + \frac{3}{2}[/latex]
  38. [latex]y = -\frac{3}{2} x +9[/latex]
  39. [latex]y = 3x-4[/latex]
  40. [latex]x=3[/latex]
  41. [latex]y=0[/latex]
  42. [latex]f(x) =2x-1[/latex], slope: [latex]m = 2[/latex], [latex]y[/latex]-intercept: [latex](0,-1)[/latex], [latex]x[/latex]-intercept: [latex]\left(\frac{1}{2}, 0 \right)[/latex]
    A line on the cartesian plane. The line intersects the horizontal axis at x=0.5 and the vertical axis at y = -1.
    Answer to Exercise 42
  43. [latex]g(t) =3-t[/latex], slope: [latex]m = -1[/latex], [latex]y[/latex]-intercept: [latex](0,3)[/latex], [latex]t[/latex]-intercept: [latex](3, 0)[/latex]
    A line on the cartesian plane. The line is decreasing left to right. The line intersects the horizontal axis at x=3 and vertical axis at y= 3.
    Answer to Exercise 43
  44. [latex]F(w) = 3[/latex], slope: [latex]m =0[/latex], [latex]y[/latex]-intercept: [latex](0,3)[/latex], [latex]w[/latex]-intercept: none
    A line on the cartesian plane the line is horizontal at y = 3.
    Answer to Exercise 44
  45. [latex]G(s) = 0[/latex], slope: [latex]m =0[/latex], [latex]y[/latex]-intercept: [latex](0,0)[/latex], [latex]s[/latex]-intercept: [latex]\{ (s,0) \, | \, s\text{ is a real number} \}[/latex]
    A horizontal line on the cartesian plane. The line runs along the x-axis.
    Answer to Exercise 45
  46. [latex]h(t) = \frac{2}{3} x + \frac{1}{3}[/latex], slope: [latex]m = \frac{2}{3}[/latex], [latex]y[/latex]-intercept: [latex]\left(0, \frac{1}{3}\right)[/latex], [latex]t[/latex]-intercept: [latex]\left(-\frac{1}{2}, 0\right)[/latex]
    A line on the cartesian plane. The line increases left to right and intersects the horizontal axis at x=-.5 and the horizontal axis at y = 1/3.
    Answer to Exercise 46
  47. [latex]h(t) = \frac{2}{3} x + \frac{1}{3}[/latex], slope: [latex]m = \frac{2}{3}[/latex], [latex]y[/latex]-intercept: [latex]\left(0, \frac{1}{3}\right)[/latex], [latex]t[/latex]-intercept: [latex]\left(-\frac{1}{2}, 0\right)[/latex]
    A line which decreases from left to right. The line intersects the horizontal axis at x = 1 and intersects the vertical axis at y =0.5.
    Answer to Exercise 47
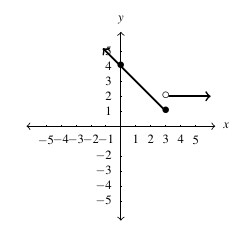
  48. domain: [latex](-\infty, \infty)[/latex], range: [latex][1, \infty)[/latex], [latex]y[/latex]-intercept: [latex](0,4)[/latex], [latex]x[/latex]-intercept: none
    The graph of a piecewise function on the cartesian plane. The first piece is a line decreasing from when x is negative infinity to the dot (3,1). The horizontal line is the second piece starts with an open circle at (3,2) and continues at y = 2 as x increases.
    Answer to Exercise 48
  49. domain: [latex](-\infty, \infty)[/latex], range: [latex][0, \infty)[/latex], [latex]y[/latex]-intercept: [latex](0,2)[/latex], [latex]x[/latex]-intercept: [latex](2,0)[/latex]
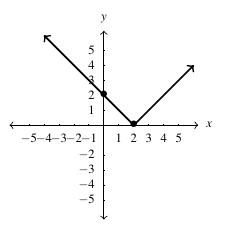
    The graph of a piecewise function. The left piece is a line decreasing to the point (2,0), while crossing the horizontal axis at y = 2. The second piece is a line that increases from the point (2,0).
    Answer to Exercise 49
  50. domain: [latex](-\infty, \infty)[/latex], range: [latex](-4, \infty)[/latex], [latex]y[/latex]-intercept: [latex](0,0)[/latex], [latex]t[/latex]-intercepts: [latex](-2,0)[/latex], [latex](0,0)[/latex]
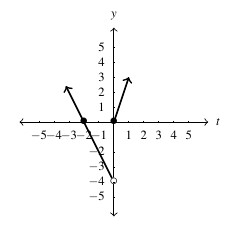
    A piecewise function graphed on a cartesian plane. The left piece is a line which decreases left to right. It intersects the horizontal axis at x = -2 and stops at the open circle (0,-4). The second piece starts at the dot (0,0) and increases left to right.
    Answer to Exercise 50
  51. domain: [latex](-\infty, \infty)[/latex], range: [latex][-3, 3][/latex], [latex]y[/latex]-intercept: [latex](0,-3)[/latex], [latex]t[/latex]-intercept: [latex]\left(\frac{3}{2}, 0 \right) = (1.5,0)[/latex]
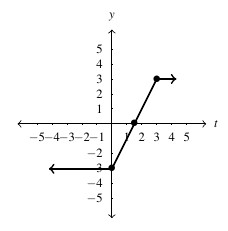
    The graph of a piecewise function. The first piece is a horizontal line at y=-3 that stops at (0,-3). The second piece is an increasing line segment that crosses the horizontal axis at x = 3/2 and stops at (3,3). The last piece is another horizontal line at y = 3.
    Answer to Exercise 51
  52. .
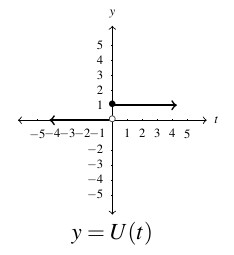
    1. A piecewise function on a cartesian plane. The left piece is a horizontal line running along the negative portion of the x-axis and stops at an open circle at (0,0). The second piece begins at the point (0,1) at a closed dot and moves horizontally as x increases.
      Answer to Exercise 52a
    2. domain: [latex](-\infty, \infty)[/latex], range: [latex]\{ 0, 1\}[/latex]
    3. [latex]U[/latex] is constant on [latex](-\infty, 0)[/latex] and [latex][0, \infty).[/latex]
    4. [latex]U(t-2) = \left\{ \begin{array}{cc} 0 & \text{if } t \text{ }2,  \\ 1 & \text{if } t \geq 2 \\ \end{array} \right.[/latex]
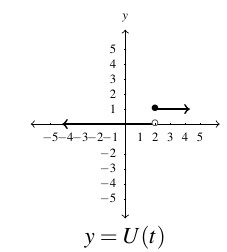
      A piecewise function on a cartesian plane. The left piece is a horizontal line running along the negative portion of the x-axis and stops at an open circle at (2,0). The second piece begins at the point (2,1) at a closed dot and moves horizontally as x increases.
      Answer to Exercise 52d
  53. [latex]f(x) = -3[/latex]

Section 1.4 Answers

  1. [latex]f(x) = |x + 4|[/latex]
    • [latex]x[/latex]-intercept [latex](-4, 0)[/latex]
    • [latex]y[/latex]-intercept [latex](0, 4)[/latex]
    • Domain [latex](-\infty, \infty)[/latex]
    • Range [latex][0, \infty)[/latex]
    • Decreasing on [latex](-\infty, -4][/latex]
    • Increasing on [latex][-4, \infty)[/latex]
    • Minimum is 0 at [latex](-4,0)[/latex]
    • No maximum
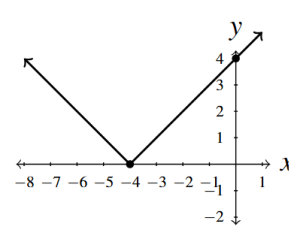
    • The rectangular plane with two rays meeting at the point (-4,0). The V opens upward.
      Answer to Exercise 1
  2. [latex]f(x) = |x| + 4[/latex]
    • No [latex]x[/latex]-intercepts
    • [latex]y[/latex]-intercept [latex](0, 4)[/latex]
    • Domain [latex](-\infty, \infty)[/latex]
    • Range [latex][4, \infty)[/latex]
    • Decreasing on [latex](-\infty, 0][/latex]
    • Increasing on [latex][0, \infty)[/latex]
    • Minimum is 4 at [latex](0,4)[/latex]
    • No maximum
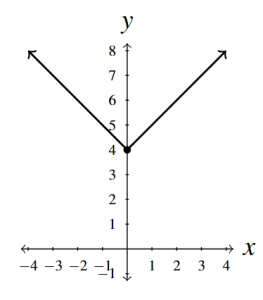
    • The rectangular plane with two rays meeting at the point (0,4). The V opens upward.
      Answer to Exercise 2
  3. [latex]f(x) = |4x|[/latex]
    • [latex]x[/latex]-intercept [latex](0, 0)[/latex]
    • [latex]y[/latex]-intercept [latex](0, 0)[/latex]
    • Domain [/latex](-\infty, \infty)[latex]
    • Range [latex][0, \infty)[/latex]
    • Decreasing on [latex](-\infty, 0][/latex]
    • Increasing on [latex][0, \infty)[/latex]
    • Minimum is 0 at [latex](0,0)[latex]
    • No maximum
    • [caption id="attachment_833" align="alignnone" width="150"]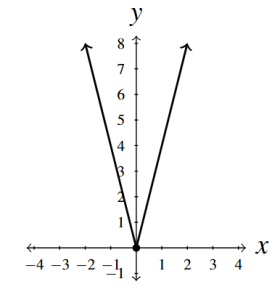The rectangular plane with two rays meeting at the point (0,0). The V opens upward. Answer to Exercise 3[/caption]
  4. [latex]g(t) = -3|t|[/latex]
    • [latex]t[/latex]-intercept [latex](0, 0)[/latex]
    • [latex]y[/latex]-intercept [latex](0, 0)[/latex]
    • Domain [latex](-\infty, \infty)[/latex]
    • Range [latex](-\infty, 0][/latex]
    • Increasing on [latex](-\infty, 0][/latex]
    • Decreasing on [latex][0, \infty)[/latex]
    • Maximum is 0 at [latex](0, 0)[/latex]
    • No minimum
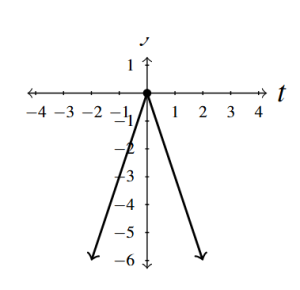
    • The rectangular plane with two rays meeting at the point (0,0). The V opens downward.
      Answer to Exercise 4
  5. [latex]g(t) = 3|t + 4| - 4[/latex]
    • [latex]t[/latex]-intercepts [latex]\left(-\frac{16}{3}, 0\right)[/latex]
    • [latex]\left(-\frac{8}{3}, 0\right)[/latex]
    • [latex]y[/latex]-intercept [latex](0, 8)[/latex]
    • Domain [latex](-\infty, \infty)[/latex]
    • Range [latex][-4, \infty)[/latex]
    • Decreasing on [latex](-\infty, -4][/latex]
    • Increasing on [latex][-4, \infty)[/latex]
    • Minimum is [latex]-4[/latex] at [latex](-4,-4)[/latex]
    • No maximum
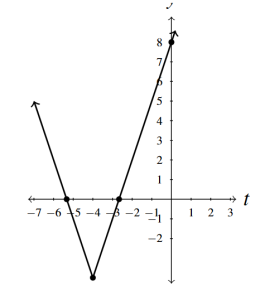
    • The rectangular plane with two rays meeting at the point (-4,-4). The V opens upward.
      Answer to Exercise 5
  6. [latex]g(t) = \frac{1}{3}|2t - 1|[/latex]
    • [latex]t[/latex]-intercepts [latex]\left(\frac{1}{2}, 0\right)[/latex]
    • [latex]y[/latex]-intercept [latex]\left(0, \frac{1}{3}\right)[/latex]
    • Domain [latex](-\infty, \infty)[/latex]
    • Range [latex][0, \infty)[/latex]
    • Decreasing on [latex]\left(-\infty, \frac{1}{2}\right][/latex]
    • Increasing on [latex]\left[\frac{1}{2}, \infty\right)[/latex]
    • Minimum is 0 at [latex]\left(\frac{1}{2},0\right)[/latex]
    • No maximum
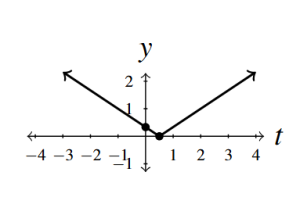
    • The rectangular plane with two rays meeting at the point (0.5,0). The V opens upward.
      Answer to Exercise 6
  7. [latex]F(x) = 2|x+1|-3[/latex]
  8. [latex]F(x) = |x-1.25|-2.75[/latex]
  9. [latex]F(x) = -|x+1|+2[/latex]
  10. [latex]F(x) = -\frac{1}{2} |x+1|+\frac{3}{2}[/latex]
  11. In each case, the graph of [latex]g[/latex] can be obtained from the graph of [latex]f[/latex] by reflecting the portion of the graph of [latex]f[/latex] which lies below the [latex]x[/latex]-axis about the [latex]x[/latex]-axis.  This meshes with Definition 1.12 because what we are doing algebraically is making the negative [latex]y[/latex]-values positive.
  12. If [latex]F(x) = a|x-h| + k[/latex], then for the vertex to be at [latex](1,-2)[/latex], [latex]h  =1[/latex] and [latex]k = -2[/latex] so [latex]F(x) = a |x-1| - 2[/latex].  Because [latex](0,-1)[/latex] is on the graph, [latex]F(0) = -1[/latex] so [latex]-1 = a|0-1|-2[/latex] which means [latex]a = 1[/latex].  This means [latex]F(x) = |x-1|-2[/latex].  However, [latex](2.6,0)[/latex] is also on the graph, so it should work out that [latex]F(2.6) = 0[/latex].  However, we find [latex]F(2.6) = |2.6-1| - 2 = -0.4 \neq 0[/latex].
    • [latex]F(x) = \left\{ \begin{array}{lr}-x-1 &  \text{if} x \leq 1,  \\\frac{5}{4} x - \frac{13}{4}  & \text{if } x \geq 1, \\\end{array} \right.[/latex]
  13. Re-write [latex]f(x) = x+|x| - 3[/latex] as [latex]\displaystyle{ f(x) = \left\{ \begin{array}{rcl} -3 & \text{ if } & x 0\\ 2x -3 & \text{ if } & x \geq 0 \\ \end{array} \right.}[/latex]
    • [latex]x[/latex]-intercept [latex]\left(\frac{3}{2}, 0\right)[/latex]
    • [latex]y[/latex]-intercept [latex](0,-3)[/latex]
    • Domain [latex](-\infty, \infty)[/latex]
    • Range [latex][-3, \infty)[/latex]
    • Increasing on [latex][0,\infty)[/latex]
    • Constant on [latex](-\infty, 0][/latex]
    • Minimum is [latex]-3[/latex] at [latex](x,-3)[/latex] where [latex]x \leq 0[/latex]
    • No maximum
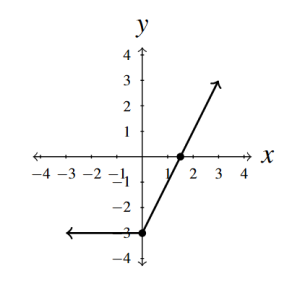
    • The rectangular plane with two rays meeting at the point (0,-3).
      Answer to Exercise 13
  14. Re-write [latex]f(x) = |x+2| - x[/latex] as [latex]\displaystyle{ f(x) = \left\{ \begin{array}{rcl} -2x-2 & \text{ if } & x -2\\ 2 & \text{ if } & x \geq -2 \\ \end{array} \right. }[/latex]
    • No [latex]x[/latex]-intercepts
    • [latex]y[/latex]-intercept [latex](0,2)[/latex]
    • Domain [latex](-\infty, \infty)[/latex]
    • Range [latex][2, \infty)[/latex]
    • Decreasing on [latex](-\infty, -2][/latex]
    • Constant on [latex][-2,\infty)[/latex]
    • Minimum is 2 at every point [latex](x,2)[/latex] where [latex]x \geq -2[/latex]
    • No maximum
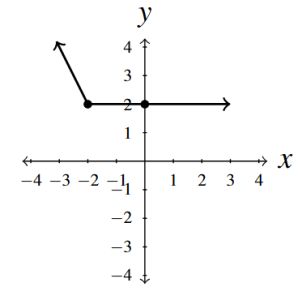
    • The rectangular plane with two rays meeting at the point (-2,2).
      Answer to Exercise 14
  15. Re-write [latex]f(x) = |x+2|-|x|[/latex] as \\ [latex]\displaystyle{ f(x) = \left\{ \begin{array}{rcl} -2 & \text{ if } & x -2\\ 2x+2 & \text{ if } & -2 \leq x 0 \\ 2 & \text{ if } & x \geq 0 \\ \end{array} \right. }[/latex]
    • [latex]x[/latex]-intercept [latex]\left(-1, 0\right)[/latex]
    • [latex]y[/latex]-intercept [latex](0,2)[/latex]
    • Domain [latex](-\infty, \infty)[/latex]
    • Range [latex][-2,2][/latex]
    • Increasing on [latex][-2,0][/latex]
    • Constant on [latex](-\infty, -2][/latex]
    • Constant on [latex][0,\infty)[/latex]
    • Minimum is [latex]-2[/latex] at [latex](x,-2)[/latex] where [latex]x \leq -2[/latex]
    • Maximum is 2 at [latex](x,2)[/latex] where [latex]x \geq 0[/latex]
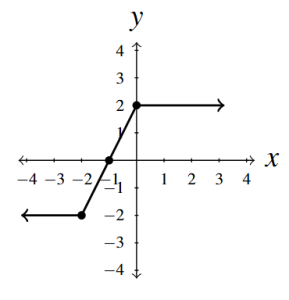
    • The rectangular plane with two rays and a line segment. The left ray meets the line segment at (-2.-2) and the right ray meets the line segment at (0,2).
      Answer to Exercise 15
  16. Re-write [latex]g(t) = |t+ 4| + |t - 2|[/latex] as [latex]\displaystyle{ g(t) = \left\{ \begin{array}{rcl}-2t - 2 & \text{ if } & t -4\\ 6 & \text{ if } & -4 \leq t 2\\  2t + 2 & \text{ if } & t \geq 2  \end{array} \right. }[/latex]
    • No [latex]t[/latex]-intercept
    • [latex]y[/latex]-intercept [latex](0, 6)[/latex]
    • Domain [latex](-\infty, \infty)[/latex]
    • Range [latex][6, \infty)[/latex]
    • Decreasing on [latex](-\infty, -4][/latex]
    • Constant on [latex][-4, 2][/latex]
    • Increasing on [latex][2, \infty)[/latex]
    • Minimum is 6 at [latex](t, 6)[/latex] where [latex]-4 \leq t \leq 2[/latex]
    • No maximum
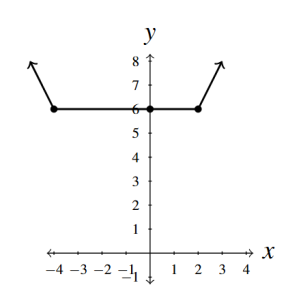
    • The rectangular plane with two rays and a line segment between. The left ray meets the line segment at (-4,6). The right ray meets the line segment at (2,6).
      Answer to Exercise 16
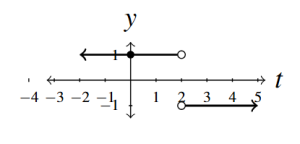
  17. Re-write [latex]g(t) = \dfrac{|t + 4|}{t + 4}[/latex] as [latex]\displaystyle{ g(t) = \left\{ \begin{array}{rcl} -1 & \text{ if } & t -4\\  1 & \text{ if } & t > -4   \end{array} \right. }[/latex]
    • No [latex]t[/latex]-intercept
    • [latex]y[/latex]-intercept [latex](0, 1)[/latex]
    • Domain [latex](-\infty, -4) \cup (-4, \infty)[/latex]
    • Range [latex]\{-1, 1\}[/latex]
    • Constant on [latex](-\infty, -4)[/latex]
    • Constant on [latex](-4, \infty)[/latex]
    • Minimum is [latex]-1[/latex] at every point [latex](t, -1)[/latex] where [latex]t -4[/latex]
    • Maximum is 1 at [latex](t, 1)[/latex] where [latex]t > -4[/latex]
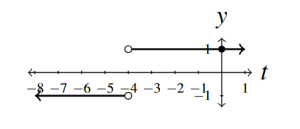
    • The rectangular plane with two separate rays. The left ray ends at (-4,-1) and the right ray starts at (-4,1).
      Answer to Exercise 17
  18. Re-write [latex]g(t) = \dfrac{|2-t|}{2-t}[/latex] as [latex]\displaystyle{ g(t) = \left\{ \begin{array}{rcl}1 & \text{ if } & t 2\\ -1 & \text{ if } & t > 2   \end{array} \right. }[/latex]
    • No [latex]t[/latex]-intercept
    • [latex]y[/latex]-intercept [latex](0, 1)[/latex]
    • Domain [latex](-\infty, 2) \cup (2, \infty)[/latex]
    • Range [latex]\{-1, 1\}[/latex]
    • Constant on [latex](-\infty, 2)[/latex]
    • Constant on [latex](2, \infty)[/latex]
    • Minimum is [latex]-1[/latex] at [latex](t, -1)[/latex] where [latex]t > 2[/latex]
    • Maximum is 1 at every point [latex](t, 1)[/latex] where [latex]t[/latex] < 2
    • The rectangular plane with two distinct rays. The left ray stops at (2,1) and the right ray starts at (2,-1).
      Answer to Exercise 18
  19. [latex]f(x) = | |x|-4|[/latex]
  20. [latex]x = -6[/latex] or [latex]x=6[/latex]
  21. [latex]x = -3[/latex] or [latex]x= \frac{11}{3}[/latex]
  22. [latex]x = -3[/latex] or [latex]x= 11[/latex]
  23. [latex]t = -1[/latex] or [latex]t= 1[/latex]
  24. [latex]t=-\frac{1}{2}[/latex] or [latex]t= \frac{1}{10}[/latex]
  25. no solution
  26. [latex]w=-3[/latex] or [latex]w= 3[/latex]
  27. [latex]w = -\frac{13}{8}[/latex] or [latex]w = \frac{53}{8}[/latex]
  28. [latex]w =-\frac{3}{2}[/latex]
  29. [latex]x=0[/latex] or [latex]x= 2[/latex]
  30. [latex]x=1[/latex]
  31. no solution
  32. [latex]x = -1[/latex] or [latex]x = 9[/latex]
  33. [latex]x = -\frac{1}{7}[/latex] or [latex]x = 1[/latex]
  34. [latex]x = 0[/latex] or [latex]x = 2[/latex]
  35. [latex]t=1[/latex]
  36. [latex]t = -\frac{3}{10}[/latex]
  37. [latex]t = \frac{1}{5}[/latex] or [latex]t = 5[/latex]
  38. [latex]\left[\frac{1}{3}, 3\right][/latex]
  39. [latex]\left(-\infty, -\frac{12}{7} \right) \cup \left(\frac{8}{7}, \infty\right)[/latex]
  40. [latex](-3,2)[/latex]
  41. [latex](-\infty,1] \cup [3,\infty)[/latex]
  42. No solution
  43. [latex](-\infty, \infty)[/latex]
  44. [latex](-3,2] \cup [6,11)[/latex]
  45. [latex][3, 4) \cup (5, 6][/latex]
  46. [latex]\left[-\frac{12}{7}, -\frac{6}{5}\right][/latex]
  47. [latex](-\infty, -4) \cup \left( \frac{2}{3}, \infty\right)[/latex]
  48. [latex]\left(-\infty, -\frac{4}{3} \right] \cup [6, \infty)[/latex]
  49. [latex](-\infty, -5)[/latex]
  50. No Solution.
  51. [latex]\left[ -7, \frac{5}{3}\right][/latex]
  52. [latex]\left( 1, \frac{5}{3} \right)[/latex]
  53. [latex](-\infty, \infty)[/latex]
  54. Answers May Vary
  55. Answers May Vary

Section 1.5 Answers

  1. For [latex]f(x) = 3x+1[/latex] and [latex]g(x) = 4-x[/latex]
    • [latex](f+g)(2) = 9[/latex]
    • [latex](f-g)(-1) = -7[/latex]
    • [latex](g-f)(1) = -1[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) = \frac{35}{4}[/latex]
    • [latex]\left(\frac{f}{g}\right)(0) = \frac{1}{4}[/latex]
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = -\frac{6}{5}[/latex]
  2. For [latex]f(x) = x^2[/latex] and [latex]g(x) = -2x+1[/latex]
    • [latex](f+g)(2) = 1[/latex]
    • [latex](f-g)(-1) = -2[/latex]
    • [latex](g-f)(1) = -2[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) = 0[/latex]
    • [latex]\left(\frac{f}{g}\right)(0) = 0[/latex]
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = \frac{5}{4}[/latex]
  3. For [latex]f(x) = x^2 - x[/latex] and [latex]g(x) = 12-x^2[/latex]
    • [latex](f+g)(2) = 10[/latex]
    • [latex](f-g)(-1) = -9[/latex]
    • [latex](g-f)(1) = 11[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) = -\frac{47}{16}[/latex]
    • [latex]\left(\frac{f}{g}\right)(0) = 0[/latex]
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = \frac{4}{3}[/latex]
  4. For [latex]f(x) = 2x^3[/latex] and [latex]g(x) = -x^2-2x-3[/latex]
    • [latex](f+g)(2) = 5[/latex]
    • [latex](f-g)(-1) = 0[/latex]
    • [latex](g-f)(1) = -8[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) = -\frac{17}{16}[/latex]
    • [latex]\left(\frac{f}{g}\right)(0) = 0[/latex]
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = \frac{3}{16}[/latex]
  5. For [latex]f(x) = \sqrt{x+3}[/latex] and [latex]g(x) = 2x-1[/latex]
    • [latex](f+g)(2) = 3+\sqrt{5}[/latex]
    • [latex](f-g)(-1) = 3+\sqrt{2}[/latex]
    • [latex](g-f)(1) = -1[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) = 0[/latex]
    • [latex]\left(\frac{f}{g}\right)(0) = -\sqrt{3}[/latex]
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = -5[/latex]
  6. For [latex]f(x) = \sqrt{4-x}[/latex] and [latex]g(x) = \sqrt{x+2}[/latex]
    • [latex](f+g)(2) = 2+\sqrt{2}[/latex]
    • [latex](f-g)(-1) = -1+\sqrt{5}[/latex]
    • [latex](g-f)(1) = 0[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) = \frac{\sqrt{35}}{2}[/latex]
    • [latex]\left(\frac{f}{g}\right)(0) = \sqrt{2}[/latex]
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = 0[/latex]
  7. For [latex]f(x) = 2x[/latex] and [latex]g(x) = \frac{1}{2x+1}[/latex]
    • [latex](f+g)(2) = \frac{21}{5}[/latex]
    • [latex](f-g)(-1) = -1[/latex]
    • [latex](g-f)(1) = -\frac{5}{3}[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) = \frac{1}{2}[/latex]
    • [latex]\left(\frac{f}{g}\right)(0) = 0[/latex]
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = \frac{1}{12}[/latex]
  8. For [latex]f(x) = x^2[/latex] and [latex]g(x) = \frac{3}{2x-3}[/latex]
    •  [latex](f+g)(2) = 7[/latex]
    • [latex](f-g)(-1) = \frac{8}{5}[/latex]
    • [latex](g-f)(1) = -4[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) = -\frac{3}{8}[/latex]
    • [latex]\left(\frac{f}{g}\right)(0) = 0[/latex]
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = -\frac{3}{28}[/latex]
  9. For [latex]f(x) = x^2[/latex] and [latex]g(x) = \frac{1}{x^2}[/latex]
    • [latex](f+g)(2) =\frac{17}{4}[/latex]
    • [latex](f-g)(-1) = 0[/latex]
    • [latex](g-f)(1) = 0[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) =1[/latex]
    • [latex]\left(\frac{f}{g}\right)(0)[/latex] is undefined.
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = \frac{1}{16}[/latex]
  10. For [latex]f(x) = x^2+1[/latex] and [latex]g(x) = \frac{1}{x^2+1}[/latex]
    • [latex](f+g)(2) =\frac{26}{5}[/latex]
    • [latex](f-g)(-1) = \frac{3}{2}[/latex]
    • [latex](g-f)(1) = -\frac{3}{2}[/latex]
    • [latex](fg)\left(\frac{1}{2}\right) =1[/latex]
    • [latex]\left(\frac{f}{g}\right)(0) = 1[/latex]
    • [latex]\left(\frac{g}{f}\right)\left(-2\right) = \frac{1}{25}[/latex]
  11. [latex](f + g)(-4) = -5[/latex]
  12. [latex](f + g)(0) = 5[/latex]
  13. [latex](f-g)(4) = -5[/latex]
  14. [latex](fg)(-4) = 6[/latex]
  15. [latex](fg)(-2) = 0[/latex]
  16. [latex](fg)(4) = -6[/latex]
  17. [latex]\left(\dfrac{f}{g}\right)(0) = \dfrac{3}{2}[/latex]
  18. [latex]\left(\dfrac{f}{g}\right)(2) = 0[/latex]
  19. [latex]\left(\dfrac{g}{f}\right)(-1) = 0[/latex]
  20. The domains of [latex]f+g[/latex], [latex]f-g[/latex] and [latex]fg[/latex] are all [latex][-4,4][/latex]. The domain of [latex]\frac{f}{g}[/latex] is [latex][-4, -1) \cup (-1,4][/latex] and the domain of [latex]\frac{g}{f}[/latex] is [latex][-4, -2) \cup (-2,2) \cup (2, 4][/latex].
  21. [latex](f + g)(-3) = 2[/latex]
  22. [latex](f - g)(2) = 3[/latex]
  23. [latex](fg)(-1) = 0[/latex]
  24. [latex](g + f)(1) = 0[/latex]
  25. [latex](g - f)(3) = 3[/latex]
  26. [latex](gf)(-3) = -8[/latex]
  27. [latex]\left(\frac{f}{g}\right)(-2)[/latex] does not exist
  28. [latex]\left(\frac{f}{g}\right)(-1) = 0[/latex]
  29. [latex]\left(\frac{f}{g}\right)(2) = 4[/latex]
  30. [latex]\left(\frac{g}{f}\right)(-1)[/latex] does not exist
  31. [latex]\left(\frac{g}{f}\right)(3) = -2[/latex]
  32. [latex]\left(\frac{g}{f}\right)(-3) = -\frac{1}{2}[/latex]
  33. For [latex]f(x) = 2x+1[/latex] and [latex]g(x) = x-2[/latex]
    • [latex](f+g)(x) = 3x-1[/latex],  Domain: [latex](-\infty, \infty)[/latex]
    • [latex](f-g)(x) = x+3[/latex],  Domain:  [latex](-\infty, \infty)[/latex]
    • [latex](fg)(x) = 2x^2-3x-2[/latex], Domain: [latex](-\infty, \infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) = \frac{2x+1}{x-2}[/latex], Domain:  [latex](-\infty, 2) \cup (2, \infty)[/latex]
  34. For [latex]f(x) = 1-4x[/latex] and [latex]g(x) = 2x-1[/latex]
    • [latex](f+g)(x) = -2x[/latex],  Domain: [latex](-\infty, \infty)[/latex]
    • [latex](f-g)(x) = 2-6x[/latex], Domain:  [latex](-\infty, \infty)[/latex]
    • [latex](fg)(x) = -8x^2+6x-1[/latex], Domain: [latex](-\infty, \infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) = \frac{1-4x}{2x-1}[/latex],  Domain:  [latex]\left(-\infty, \frac{1}{2} \right) \cup \left(\frac{1}{2}, \infty \right)[/latex]
  35. For [latex]f(x) = x^2[/latex] and [latex]g(x) = 3x-1[/latex]
    • [latex](f+g)(x) = x^2+3x-1[/latex], Domain: [latex](-\infty, \infty)[/latex]
    • [latex](f-g)(x) = x^2-3x+1[/latex], Domain:  [latex](-\infty, \infty)[/latex]
    • [latex](fg)(x) = 3x^3-x^2[/latex], Domain: [latex](-\infty, \infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) = \frac{x^2}{3x-1}[/latex], Domain:  [latex]\left(-\infty, \frac{1}{3} \right) \cup \left(\frac{1}{3}, \infty \right)[/latex]
  36. For [latex]f(x) = x^2-x[/latex] and [latex]g(x) = 7x[/latex]
    • [latex](f+g)(x) = x^2+6x[/latex], Domain: [latex](-\infty, \infty)[/latex]
    • [latex](f-g)(x) = x^2-8x[/latex], Domain:  [latex](-\infty, \infty)[/latex]
    • [latex](fg)(x) = 7x^3-7x^2[/latex], Domain: [latex](-\infty, \infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) = \frac{x-1}{7}[/latex],  Domain:  [latex]\left(-\infty, 0 \right) \cup \left(0, \infty \right)[/latex]
  37. For [latex]f(x) = x^2-4[/latex] and [latex]g(x) = 3x+6[/latex]
    • [latex](f+g)(x) = x^2+3x+2[/latex],  Domain: [latex](-\infty, \infty)[/latex]
    • [latex](f-g)(x) = x^2-3x-10[/latex], Domain:  [latex](-\infty, \infty)[/latex]
    • [latex](fg)(x) = 3x^3+6x^2-12x-24[/latex], Domain: [latex](-\infty, \infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) = \frac{x-2}{3}[/latex], Domain:  [latex]\left(-\infty, -2 \right) \cup \left(-2, \infty \right)[/latex]
  38. For [latex]f(x) = -x^2+x+6[/latex] and [latex]g(x) = x^2-9[/latex]
    • [latex](f+g)(x) = x-3[/latex],  Domain: [latex](-\infty, \infty)[/latex]
    • [latex](f-g)(x) = -2x^2+x+15[/latex], Domain:  [latex](-\infty, \infty)[/latex]
    • [latex](fg)(x) = -x^4+x^3+15x^2-9x-54[/latex], Domain: [latex](-\infty, \infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) = -\frac{x+2}{x+3}[/latex],  Domain:  [latex]\left(-\infty, -3 \right) \cup \left(-3, 3 \right) \cup (3, \infty)[/latex]
  39. For  [latex]f(x) = \frac{x}{2}[/latex] and [latex]g(x) = \frac{2}{x}[/latex]
    • [latex](f+g)(x) = \frac{x^2+4}{2x}[/latex],  Domain: [latex](-\infty, 0) \cup (0, \infty)[/latex]
    • [latex](f-g)(x) = \frac{x^2-4}{2x}[/latex], Domain:  [latex](-\infty,0) \cup (0, \infty)[/latex]
    • [latex](fg)(x) = 1[/latex], Domain: [latex](-\infty,0) \cup (0, \infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) = \frac{x^2}{4}[/latex],  Domain: [latex](-\infty,0) \cup (0, \infty)[/latex]
  40. For   [latex]f(x) =x-1[/latex] and [latex]g(x) = \frac{1}{x-1}[/latex]
    • [latex](f+g)(x) = \frac{x^2-2x+2}{x-1}[/latex], Domain: [latex](-\infty, 1) \cup (1, \infty)[/latex]
    • [latex](f-g)(x) = \frac{x^2-2x}{x-1}[/latex], Domain:  [latex](-\infty,1) \cup (1, \infty)[/latex]
    • [latex](fg)(x) = 1[/latex], Domain: [latex](-\infty,1) \cup (1, \infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) =x^2-2x+1[/latex], Domain: [latex](-\infty,1) \cup (1, \infty)[/latex]
  41. For   [latex]f(x) =x[/latex] and [latex]g(x) = \sqrt{x+1}[/latex]
    • [latex](f+g)(x) = x+\sqrt{x+1}[/latex], Domain: [latex][-1,\infty)[/latex]
    • [latex](f-g)(x) = x-\sqrt{x+1}[/latex], Domain: [latex][-1,\infty)[/latex]
    • [latex](fg)(x) = x\sqrt{x+1}[/latex], Domain: [latex][-1,\infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) =\frac{x}{\sqrt{x+1}}[/latex],  Domain: [latex](-1,\infty)[/latex]
  42. For   [latex]f(x) = \sqrt{x-5}[/latex] and [latex]g(x) = f(x) = \sqrt{x-5}[/latex]
    • [latex](f+g)(x) = 2\sqrt{x-5}[/latex],  Domain: [latex][5,\infty)[/latex]
    • [latex](f-g)(x) =0[/latex],  Domain: [latex][5,\infty)[/latex]
    • [latex](fg)(x) =x-5[/latex], Domain: [latex][5,\infty)[/latex]
    • [latex]\left(\frac{f}{g}\right)(x) =1[/latex],  Domain: [latex](5,\infty)[/latex]
  43. One solution is [latex]f(z) = 4z[/latex] and [latex]g(z) = z^3[/latex].
  44. One solution is [latex]f(z) = 4z[/latex] and [latex]g(z) = - z^3[/latex].
  45. One solution is [latex]f(t) = 3t[/latex] and [latex]h(t) = |2t-1|[/latex].
  46. One solution is [latex]f(x) = 3-x[/latex] and [latex]g(x) = x+1[/latex].
  47. One solution is [latex]f(x) = 3-x[/latex] and [latex]g(x) = (x+1)^{-1}[/latex].
  48. No. The equivalence does not hold when [latex]x = 0[/latex].
  49. For  [latex]f(x) = x^2[/latex] and [latex]g(t) = 2t+1[/latex]
    • [latex](g\circ f)(0) = 1[/latex]
    • [latex](f\circ g)(-1) = 1[/latex]
    • [latex](f \circ f)(2) = 16[/latex]
    • [latex](g\circ f)(-3) = 19[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = 4[/latex]
    • [latex](f \circ f)(-2) = 16[/latex]
  50. For   [latex]f(x) = 4-x[/latex] and [latex]g(t) = 1-t^2[/latex]
    • [latex](g\circ f)(0) = -15[/latex]
    • [latex](f\circ g)(-1) = 4[/latex]
    • [latex](f \circ f)(2) = 2[/latex]
    • [latex](g\circ f)(-3) = -48[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = \frac{13}{4}[/latex]
    • [latex](f \circ f)(-2) = -2[/latex]
  51. For   [latex]f(x) = 4-3x[/latex] and  [latex]g(t) = |t|[/latex]
    • [latex](g\circ f)(0) = 4[/latex]
    • [latex](f\circ g)(-1) = 1[/latex]
    • [latex](f \circ f)(2) = 10[/latex]
    • [latex](g\circ f)(-3) = 13[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = \frac{5}{2}[/latex]
    • [latex](f \circ f)(-2) = -26[/latex]
  52. For   [latex]f(x) = |x-1|[/latex] and [latex]g(t) = t^2-5[/latex]
    • [latex](g\circ f)(0) = -4[/latex]
    • [latex](f\circ g)(-1) = 5[/latex]
    • [latex](f \circ f)(2) = 0[/latex]
    • [latex](g\circ f)(-3) = 11[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = \frac{23}{4}[/latex]
    • [latex](f \circ f)(-2) = 2[/latex]
  53. For [latex]f(x) = 4x+5[/latex] and [latex]g(t) = \sqrt{t}[/latex]
    • [latex](g\circ f)(0) = \sqrt{5}[/latex]
    • [latex](f\circ g)(-1)[/latex] is not real
    • [latex](f \circ f)(2) = 57[/latex]
    • [latex](g\circ f)(-3)[/latex] is not real
    • [latex](f\circ g)\left(\frac{1}{2}\right) = 5+2\sqrt{2}[/latex]
    • [latex](f \circ f)(-2) = -7[/latex]
  54. For [latex]f(x) = \sqrt{3-x}[/latex] and [latex]g(t) = t^2+1[/latex]
    • [latex](g\circ f)(0) = 4[/latex]
    • [latex](f\circ g)(-1) = 1[/latex]
    • [latex](f \circ f)(2) = \sqrt{2}[/latex]
    • [latex](g\circ f)(-3) = 7[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = \frac{\sqrt{7}}{2}[/latex]
    • [latex](f \circ f)(-2) = \sqrt{3 - \sqrt{5}}[/latex]
  55. For  [latex]f(x) = 6-x-x^2[/latex] and [latex]g(t) = t\sqrt{t+10}[/latex]
    • [latex](g\circ f)(0) = 24[/latex]
    • [latex](f\circ g)(-1) = 0[/latex]
    • [latex](f \circ f)(2) = 6[/latex]
    • [latex](g\circ f)(-3) = 0[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = \frac{27-2\sqrt{42}}{8}[/latex]
    • [latex](f \circ f)(-2) = -14[/latex]
  56. For  [latex]f(x) = \sqrt[3]{x+1}[/latex] and [latex]g(t) = 4t^2-t[/latex]
    • [latex](g\circ f)(0) = 3[/latex]
    • [latex](f\circ g)(-1) = \sqrt[3]{6}[/latex]
    • [latex](f \circ f)(2) = \sqrt[3]{\sqrt[3]{3}+1}[/latex]
    • [latex](g\circ f)(-3) = 4\sqrt[3]{4}+\sqrt[3]{2}[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = \frac{\sqrt[3]{12}}{2}[/latex]
    • [latex](f \circ f)(-2) = 0[/latex]
  57. For  [latex]f(x) = \frac{3}{1-x}[/latex] and [latex]g(t) = \frac{4t}{t^2+1}[/latex]
    • [latex](g\circ f)(0) = \frac{6}{5}[/latex]
    • [latex](f\circ g)(-1) = 1[/latex]
    • [latex](f \circ f)(2) = \frac{3}{4}[/latex]
    • [latex](g\circ f)(-3) = \frac{48}{25}[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = -5[/latex]
    • [latex](f \circ f)(-2)[/latex] is undefined
  58. For  [latex]f(x) = \frac{x}{x+5}[/latex] and [latex]g(t) = \frac{2}{7-t^2}[/latex]
    • [latex](g\circ f)(0) = \frac{2}{7}[/latex]
    • [latex](f\circ g)(-1) = \frac{1}{16}[/latex]
    • [latex](f \circ f)(2) = \frac{2}{37}[/latex]
    • [latex](g\circ f)(-3) = \frac{8}{19}[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = \frac{8}{143}[/latex]
    • [latex](f \circ f)(-2) = -\frac{2}{13}[/latex]
  59. For  [latex]f(x) = \frac{2x}{5-x^2}[/latex] and [latex]g(t) = \sqrt{4t+1}[/latex]
    • [latex](g\circ f)(0) = 1[/latex]
    • [latex](f\circ g)(-1)[/latex] is not real
    • [latex](f \circ f)(2) = -\frac{8}{11}[/latex]
    • [latex](g\circ f)(-3) = \sqrt{7}[/latex]
    • [latex](f\circ g)\left(\frac{1}{2}\right) = \sqrt{3}[/latex]
    • [latex](f \circ f)(-2) = \frac{8}{11}[/latex]
  60. For  [latex]f(x) =\sqrt{2x+5}[/latex] and [latex]g(t) = \frac{10t}{t^2+1}[/latex]
    • [latex](g\circ f)(0) = \frac{5\sqrt{5}}{3}[/latex]
    • [latex](f\circ g)(-1)[/latex] is not real
    • [latex](f \circ f)(2) = \sqrt{11}[/latex]
    • [latex](g\circ f)(-3)[/latex] is not real
    • [latex](f\circ g)\left(\frac{1}{2}\right) = \sqrt{13}[/latex]
    • [latex](f \circ f)(-2) = \sqrt{7}[/latex]
  61. For [latex]f(x) = 2x+3[/latex] and [latex]g(t) = t^2-9[/latex]
    • [latex](g \circ f)(x) = 4x^2+12x[/latex], domain: [latex](-\infty, \infty)[/latex]
    • [latex](f \circ g)(t) = 2t^2-15[/latex], domain: [latex](-\infty, \infty)[/latex]
    • [latex](f \circ f)(x) = 4x+9[/latex], domain: [latex](-\infty, \infty)[/latex]
  62. For  [latex]f(x) = x^2 -x+1[/latex] and [latex]g(t) = 3t-5[/latex]
    • [latex](g \circ f)(x) = 3x^2-3x-2[/latex], domain: [latex](-\infty, \infty)[/latex]
    • [latex](f \circ g)(t) =9t^2-33t+31[/latex], domain: [latex](-\infty, \infty)[/latex]
    • [latex](f \circ f)(x) = x^4-2x^3+2x^2-x+1[/latex], domain: [latex](-\infty, \infty)[/latex]
  63. For  [latex]f(x) = x^2-4[/latex] and [latex]g(t) = |t|[/latex]
    • [latex](g \circ f)(x) = |x^2-4|[/latex], domain: [latex](-\infty, \infty)[/latex]
    • [latex](f \circ g)(t) =|t|^2-4 = t^2-4[/latex], domain: [latex](-\infty, \infty)[/latex]
    • [latex](f \circ f)(x) =x^4-8x^2+12[/latex], domain: [latex](-\infty, \infty)[/latex]
  64. For   [latex]f(x) = 3x-5[/latex] and [latex]g(t) = \sqrt{t}[/latex]
    • [latex](g \circ f)(x) = \sqrt{3x-5}[/latex], domain: [latex]\left[ \frac{5}{3}, \infty \right)[/latex]
    • [latex](f \circ g)(t) = 3\sqrt{t}-5[/latex], domain: [latex][0,\infty)[/latex]
    • [latex](f \circ f)(x) = 9x-20[/latex], domain: [latex](-\infty, \infty)[/latex]
  65. For   [latex]f(x) = |x+1|[/latex] and [latex]g(t) = \sqrt{t}[/latex]
    • [latex](g \circ f)(x) = \sqrt{|x+1|}[/latex], domain: [latex](-\infty, \infty)[/latex]
    • [latex](f \circ g)(t) = |\sqrt{t}+1| = \sqrt{t}+1[/latex], domain: [latex][0,\infty)[/latex]
    • [latex](f \circ f)(x) = ||x+1|+1| = |x+1|+1[/latex], domain: [latex](-\infty, \infty)[/latex]
  66. For   [latex]f(x) = 3-x^2[/latex] and [latex]g(t) = \sqrt{t+1}[/latex]
    • [latex](g \circ f)(x) = \sqrt{4-x^2}[/latex], domain: [latex][-2,2][/latex]
    • [latex](f \circ g)(t) =2-t[/latex], domain: [latex][-1, \infty)[/latex]
    • [latex](f \circ f)(x) = -x^4+6x^2-6[/latex], domain: [latex](-\infty, \infty)[/latex]
  67. For   [latex]f(x) = |x|[/latex] and [latex]g(t) = \sqrt{4-t}[/latex]
    • [latex](g \circ f)(x) = \sqrt{4-|x|}[/latex], domain: [latex][-4,4][/latex]
    • [latex](f \circ g)(t) =|\sqrt{4-t}| = \sqrt{4-t}[/latex], domain: [latex](-\infty, 4][/latex]
    • [latex](f \circ f)(x) = | |x| | = |x|[/latex], domain: [latex](-\infty, \infty)[/latex]
  68. For  [latex]f(x) = x^2-x-1[/latex] and [latex]g(t) = \sqrt{t-5}[/latex]
    • [latex](g \circ f)(x) = \sqrt{x^2-x-6}[/latex], domain: [latex](-\infty, -2] \cup [3,\infty)[/latex]
    • [latex](f \circ g)(t) =t-6-\sqrt{t-5}[/latex], domain: [latex][5,\infty)[/latex]
    • [latex](f \circ f)(x) =x^4-2x^3-2x^2+3x+1[/latex], domain: [latex](-\infty, \infty)[/latex]
  69. For   [latex]f(x) = 3x-1[/latex] and [latex]g(t) = \frac{1}{t+3}[/latex]
    • [latex](g \circ f)(x) = \frac{1}{3x+2}[/latex], domain: [latex]\left(-\infty, -\frac{2}{3}\right) \cup \left(-\frac{2}{3}, \infty\right)[/latex]
    • [latex](f \circ g)(t) = -\frac{t}{t+3}[/latex], domain: [latex]\left(-\infty, -3\right) \cup \left(-3, \infty\right)[/latex]
    • [latex](f \circ f)(x) = 9x-4[/latex], domain: [latex](-\infty, \infty)[/latex]
  70. For   [latex]f(x) = \frac{3x}{x-1}[/latex] and [latex]g(t) =\frac{t}{t-3}[/latex]
    • [latex](g \circ f)(x) =x[/latex], domain: [latex]\left(-\infty, 1\right) \cup (1, \infty)[/latex]
    • [latex](f \circ g)(t) =t[/latex], domain:  [latex]\left(-\infty, 3\right) \cup (3,\infty)[/latex]
    • [latex](f \circ f)(x) = \frac{9x}{2x+1}[/latex], domain: [latex]\left(-\infty, -\frac{1}{2}\right) \cup \left(-\frac{1}{2}, 1 \right) \cup \left(1,\infty \right)[/latex]
  71. For    [latex]f(x) = \frac{x}{2x+1}[/latex] and [latex]g(t) = \frac{2t+1}{t}[/latex]
    • [latex](g \circ f)(x) = \frac{4x+1}{x}[/latex], domain: [latex]\left(-\infty, -\frac{1}{2}\right) \cup \left(-\frac{1}{2}, 0), \cup (0, \infty\right)[/latex]
    • [latex](f \circ g)(t) = \frac{2t+1}{5t+2}[/latex], domain:  [latex]\left(-\infty, -\frac{2}{5}\right) \cup \left(-\frac{2}{5}, 0\right) \cup (0,\infty)[/latex]
    • [latex](f \circ f)(x) = \frac{x}{4x+1}[/latex], domain: [latex]\left(-\infty, -\frac{1}{2}\right) \cup \left(-\frac{1}{2}, -\frac{1}{4} \right) \cup \left(-\frac{1}{4},\infty\right)[/latex]
  72. For  [latex]f(x) = \frac{2x}{x^2-4}[/latex] and [latex]g(t) =\sqrt{1-t}[/latex]
    • [latex](g \circ f)(x) =\sqrt{\frac{x^2-2x-4}{x^2-4}}[/latex], domain: [latex]\left(-\infty, -2\right) \cup \left[1-\sqrt{5}, 2\right) \cup \left[1+\sqrt{5}, \infty\right)[/latex]
    • [latex](f \circ g)(t) = -\frac{2\sqrt{1-t}}{t+3}[/latex], domain: [latex]\left(-\infty, -3\right) \cup \left(-3, 1\right][/latex]
    • [latex](f \circ f)(x) = \frac{4x-x^3}{x^4-9x^2+16}[/latex], domain: [latex]\left(-\infty, -\frac{1+\sqrt{17}}{2}\right) \cup \left(-\frac{1+\sqrt{17}}{2}, -2\right) \cup \left(-2, \frac{1-\sqrt{17}}{2}\right) \cup \left(\frac{1-\sqrt{17}}{2}, \frac{-1+\sqrt{17}}{2}\right) \cup \left(\frac{-1+\sqrt{17}}{2}, 2\right) \cup \left(2, \frac{1+\sqrt{17}}{2} \right) \cup \left(\frac{1+\sqrt{17}}{2}, \infty\right)[/latex]
  73. [latex](h\circ g \circ f)(x)= |\sqrt{-2x}|= \sqrt{-2x}[/latex], domain: [latex](-\infty, 0][/latex]
  74. [latex](h\circ f \circ g)(t) = |-2\sqrt{t}|= 2\sqrt{t}[/latex], domain: [latex][0,\infty)[/latex]
  75. [latex](g\circ f \circ h)(s) = \sqrt{-2|s|}[/latex], domain: [latex]\{0\}[/latex]
  76. [latex](g\circ h \circ f)(x) = \sqrt{|-2x|} = \sqrt{2|x|}[/latex], domain: [latex](-\infty, \infty)[/latex]
  77. [latex](f\circ h \circ g)(t) = -2|\sqrt{t}| = -2\sqrt{t}[/latex], domain: [latex][0,\infty)[/latex]
  78. [latex](f\circ g \circ h)(s) = -2\sqrt{|s|}[/latex], , domain: [latex](-\infty,\infty)[/latex]
  79. [latex](f \circ g)(3)= f(g(3)) = f(2) = 4[/latex]
  80. [latex]f(g(-1)) = f(-4)[/latex] which is undefined
  81. [latex](f \circ f)(0) = f(f(0)) = f(1) = 3[/latex]
  82. [latex](f \circ g)(-3) = f(g(-3)) = f(-2) = 2[/latex]
  83. (g \circ f)(3) = g(f(3)) = g(-1) = -4$
  84. [latex]g(f(-3)) = g(4)[/latex] which is undefined
  85. (g \circ g)(-2) = g(g(-2)) = g(0) = 0$
  86. [latex](g \circ f)(-2) = g(f(-2)) = g(2) = 1[/latex]
  87. [latex]g(f(g(0))) = g(f(0)) = g(1) = -3[/latex]
  88. [latex]f(f(f(-1))) = f(f(0)) = f(1) = 3[/latex]
  89. [latex]f(f(f(f(f(1))))) = f(f(f(f(3)))) =\\ f(f(f(-1))) = f(f(0))  = f(1) = 3[/latex]
  90. [latex]\underbrace{(g \circ g \circ \cdots \circ g)}_{n \text{ times}}(0) = 0[/latex]
  91. .
    • The domain of [latex]f \circ g[/latex] is [latex]\{ -3, -2, 0, 1, 2, 3\}[/latex] and the range of [latex]f \circ g[/latex] is [latex]\{1, 2, 3, 4\}[/latex].
    • The domain of [latex]g \circ f[/latex] is [latex]\{ -2, -1, 0, 1, 3 \}[/latex] and the range of [latex]g \circ f[/latex] is [latex]\{ -4, -3, 0, 1, 2 \}[/latex].
  92. [latex](g\circ f)(1) = 3[/latex]
  93. [latex](f \circ g)(3) = 1[/latex]
  94. [latex](g\circ f)(2) = 0[/latex]
  95. [latex](f\circ g)(0) = 1[/latex]
  96. [latex](f\circ f)(4) = 1[/latex]
  97. [latex](g \circ g)(1) = 0[/latex]
  98. .
    • The domain of [latex]f \circ g[/latex] is [latex][0,3][/latex] and the range of [latex]f \circ g[/latex] is [latex][1, 4.5][/latex].
    • The domain of [latex]g \circ f[/latex] is [latex][0,2] \cup [3,4][/latex] and the range is [latex][0,3][/latex].
  99. Let [latex]f(x) = 2x+3[/latex] and [latex]g(x) = x^3[/latex], then [latex]p(x) = (g\circ f)(x)[/latex].
  100. Let [latex]f(x) = x^2-x+1[/latex] and [latex]g(x) = x^5[/latex], [latex]P(x) =(g\circ f)(x)[/latex].
  101. Let [latex]f(t) = 2t-1[/latex] and [latex]g(t) = \sqrt{t}[/latex], then [latex]h(t) = (g\circ f)(t)[/latex].
  102. Let [latex]f(t) = 7-3t[/latex] and [latex]g(t) = |t|[/latex], then [latex]H(t) = (g\circ f)(t)[/latex].
  103. Let [latex]f(s) = 5s+1[/latex] and [latex]g(s) = \frac{2}{s}[/latex], then [latex]r(s) =(g\circ f)(s)[/latex].
  104. Let [latex]f(s) = s^2-1[/latex] and [latex]g(s) = \frac{7}{s}[/latex], then [latex]R(s) =(g\circ f)(s)[/latex].
  105. Let [latex]f(z) = |z|[/latex] and [latex]g(z) = \frac{z+1}{z-1}[/latex], then [latex]q(z) =(g\circ f)(z)[/latex].
  106. Let [latex]f(z) = z^3[/latex] and [latex]g(z)= \frac{2z+1}{z-1}[/latex], then [latex]Q(z) =(g\circ f)(z)[/latex].
  107. Let [latex]f(x) =2x[/latex] and [latex]g(x) = \frac{x+1}{3-2x}[/latex], then [latex]v(x) =(g\circ f)(x)[/latex].
  108. Let [latex]f(x) = x^2[/latex] and [latex]g(x) = \frac{x}{x^2+1}[/latex], then [latex]w(x) =(g\circ f)(x)[/latex].
  109. [latex]F(x) = \sqrt{\frac{x^{3} + 6}{x^{3} - 9}} = (h(g(f(x)))[/latex] where [latex]f(x) = x^{3}, \, g(x) = \frac{x + 6}{x - 9}[/latex] and [latex]h(x) = \sqrt{x}[/latex]
  110. [latex]F(x) = 3\sqrt{-x + 2} - 4 = k(j(f(h(g(x)))))[/latex]
  111. One solution is [latex]F(x) = -\frac{1}{2}(2x - 7)^{3} + 1 = k(j(f(h(g(x)))))[/latex] where [latex]g(x) = 2x, \, h(x) = x - 7, \, j(x) = -\frac{1}{2}x[/latex] and [latex]k(x) = x + 1[/latex]. You could also have [latex]F(x) = H(f(G(x)))[/latex] where [latex]G(x) = 2x - 7[/latex] and [latex]H(x) = -\frac{1}{2}x + 1[/latex].
  112. [latex]\displaystyle{(f \circ g)(x) = \left\{\begin{array}{cc} 6x-2 & \text{if } x \leq 3 \\ 13-3x & \text{if } x > 3 \\ \end{array} \right.}[/latex] and [latex]\displaystyle{(g \circ f)(x) = \left\{\begin{array} 6x+1 & \text{if } x \leq \frac{2}{3} \\ 3-3x & \text{if } x > \frac{2}{3} \\ \end{array} \right.}[/latex]
  113. [latex]V(x) = x^{3}[/latex] so [latex]V(x(t)) = (t + 1)^{3}[/latex]
  114. .
    • [latex]R(x) = 2x[/latex]
    • [latex]\left(R \circ x \right)(t) =  -8t^2+40t+184[/latex], [latex]0 \leq t \leq 4[/latex].  This gives the revenue per hour as a function of time.
    • Noon corresponds to [latex]t=2[/latex], so [latex]\left(R \circ x \right)(2) = 232[/latex].  The hourly revenue at noon is $232 per hour.

Section 1.6 Answers

  1. [latex](2,0)[/latex]
  2. [latex](-1,-3)[/latex]
  3. [latex](2,-4)[/latex]
  4. [latex](3,-3)[/latex]
  5. [latex](2,-9)[/latex]
  6. [latex]\left(\frac{2}{3}, -3\right)[/latex]
  7. [latex](2,3)[/latex]
  8. [latex](-2,-3)[/latex]
  9. [latex](5,-2)[/latex]
  10. [latex](1,-6)[/latex]
  11. [latex](2,13)[/latex]
  12. [latex]y = (1,-10)[/latex]
  13. [latex]\left(2, -\frac{3}{2}\right)[/latex]
  14. [latex]\left(\frac{1}{2}, -12 \right)[/latex]
  15. [latex](-1,-7)[/latex]
  16. [latex]\left(-\frac{1}{2}, -3\right)[/latex]
  17. [latex]\left(\frac{2}{3}, -2 \right)[/latex]
  18. [latex](1,1)[/latex]
  19. [latex]y = f(x) + 1[/latex]
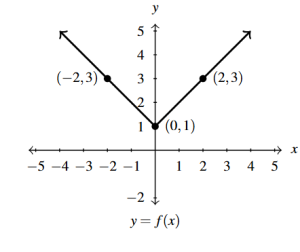
    The rectangular plane with the graph of f(x) shifted up 1 unit.
    Answer to Exercise 19
  20. [latex]y = f(x) - 2[/latex]
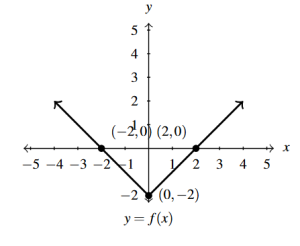
    The rectangular plane with the graph of f(x) shifted down 2 units.
    Answer to Exercise 20
  21. [latex]y = f(x+1)[/latex]
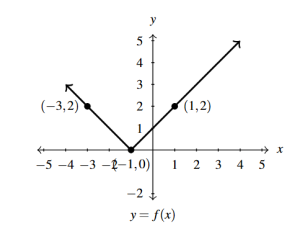
    The rectangular plane with the graph of f(x) shifted left 1 unit.
    Answer to Exercise 21
  22. [latex]y = f(x - 2)[/latex]
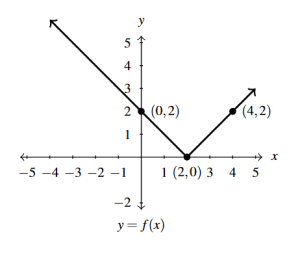
    The rectangular plane with the graph of f(x) shifted right 2 units.
    Answer to Exercise 22
  23. [latex]y = 2f(x)[/latex]
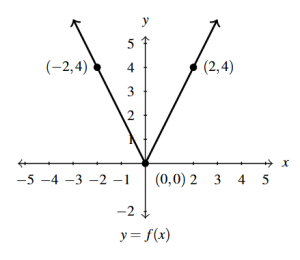
    The rectangular plane with the graph of f(x) vertically scaled by a factor of 2.
    Answer to Exercise 23
  24. [latex]y = f(2x)[/latex]
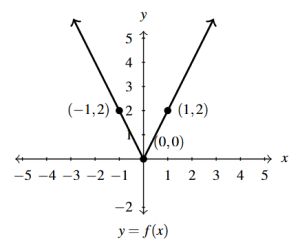
    The rectangular plane with the graph of f(x) horizontally scaled by a factor of 1/2.
    Answer to Exercise 24
  25. [latex]y = 2 - f(x)[/latex]
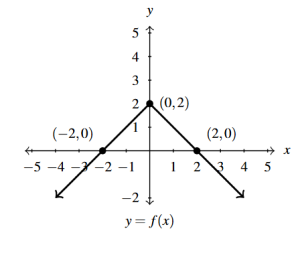
    The rectangular plane with the graph of f(x) reflected over the x-axis and then shifted up 2 unit.
    Answer to Exercise 25
  26. [latex]y = f(2-x)[/latex]
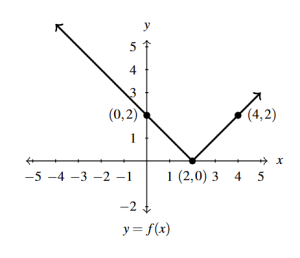
    The rectangular plane with the graph of f(x) shifted left 2 unit and then reflected across the y-axis..
    Answer to Exercise 26
  27. [latex]y = 2-f(2-x)[/latex]
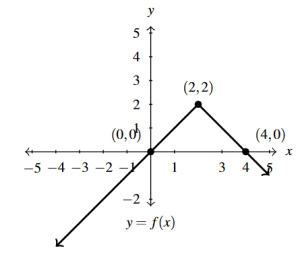
    The rectangular plane with the graph of f(x) shifted left 2 units, then reflected across the y-axis, next reflected across the x-axis and last shifted up 2 unit.
    Answer to Exercise 27
  28. Answers left to Students
  29. Answers left to Students
  30. [latex]y = g(t) - 1[/latex]
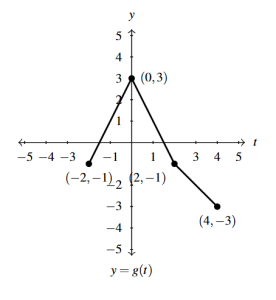
    The rectangular plane with the graph of g(t) shifted down 1 unit.
    Answer to Exercise 30
  31. [latex]y = g(t + 1)[/latex]
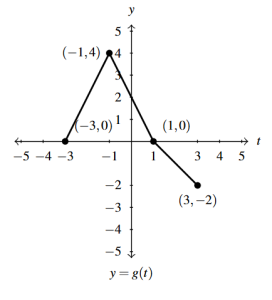
    The rectangular plane with the graph of g(t) shifted left 1 unit.
    Answer to Exercise 31
  32. [latex]y = \frac{1}{2} g(t)[/latex]
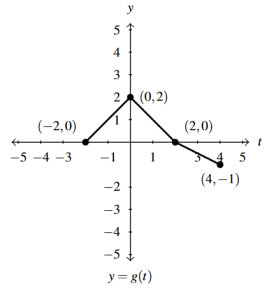
    The rectangular plane with the graph of g(t) vertically scaled by a factor of 1/2.
    Answer to Exercise 32
  33. [latex]y =g(2t)[/latex]
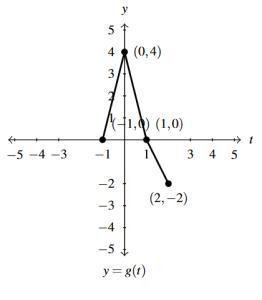
    The rectangular plane with the graph of g(t) horizontally scaled by a factor of 1/2.
    Answer to Exercise 33
  34. [latex]y = - g(t)[/latex]
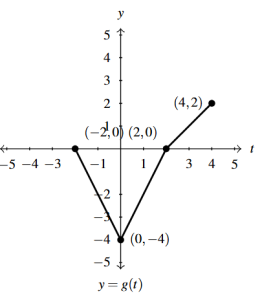
    The rectangular plane with the graph of g(t) reflected across the x-axis.
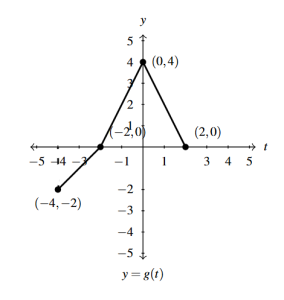
    Answer to Exercise 34
  35. [latex]y = g(-t)[/latex]
    The rectangular plane with the graph of g(t) reflected across the y-axis.
    Answer to Exercise 35
  36. [latex]y = g(t+1) - 1[/latex]
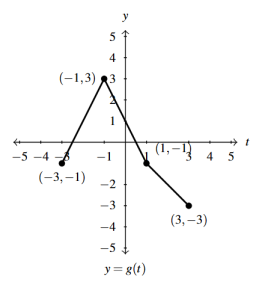
    The rectangular plane with the graph of g(t) shifted left 1 unit and then shifted down 1 unit.
    Answer to Exercise 36
  37. [latex]y = 1 -g(t)[/latex]
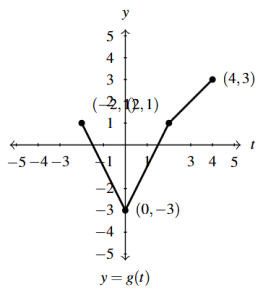
    The rectangular plane with the graph of g(t) reflected across the x-axis and then shifted up 1 unit.
    Answer to Exercise 37
  38. [latex]y = \frac{1}{2}g(t+1)-1[/latex]
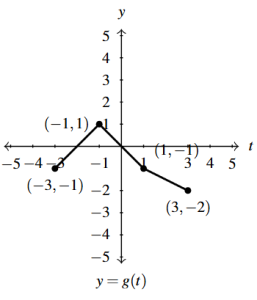
    The rectangular plane with the graph of g(t) shifted left 1 unit, then vertically scaled by a factor of 1/2, and last shifted down 1 unit.
    Answer to Exercise 38
  39. [latex]g(x) = f(x) + 3[/latex]
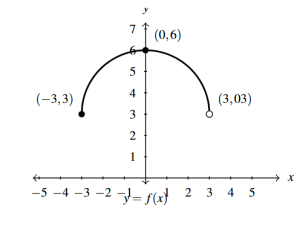
    The rectangular plane with the graph of f(x) shifted up 3 units.
    Answer to Exercise 39
  40. [latex]h(x) = f(x) - \frac{1}{2}[/latex]
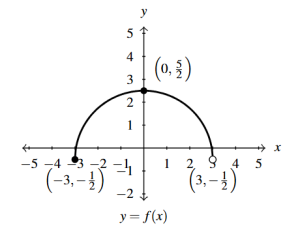
    The rectangular plane with the graph of f(x) shifted down 0.5 units.
    Answer to Exercise 40
  41. [latex]j(x) = f\left(x - \frac{2}{3}\right)[/latex]
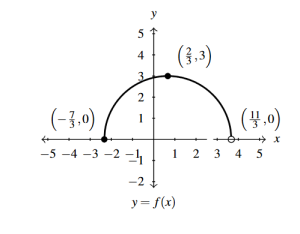
    The rectangular plane with the graph of f(x) shifted right 2/3 units.
    Answer to Exercise 41
  42. [latex]a(x) = f(x + 4)[/latex]
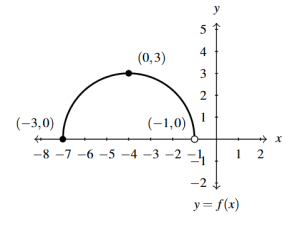
    The rectangular plane with the graph of f(x) shifted left 4 units.
    Answer to Exercise 42
  43. [latex]b(x) = f(x + 1) - 1[/latex]
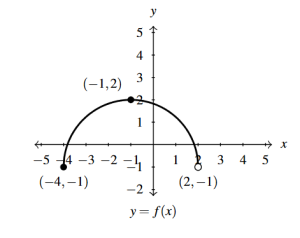
    The rectangular plane with the graph of f(x) shifted left 1 unit and shifted down 1 unit.
    Answer to Exercise 43
  44. [latex]c(x) = \frac{3}{5}f(x)[/latex]
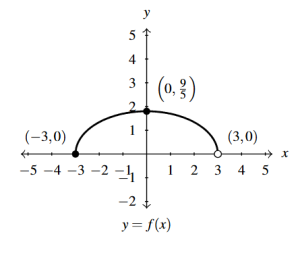
    The rectangular plane with the graph of f(x) vertically scaled by a factor of 3/5.
    Answer to Exercise 44
  45. [latex]d(x) = -2f(x)[/latex]
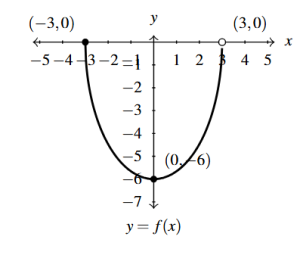
    The rectangular plane with the graph of f(x) vertically scaled by a factor of 2 and then reflected across the x-axis.
    Answer to Exercise 45
  46. [latex]k(x) = f\left(\frac{2}{3}x\right)[/latex]
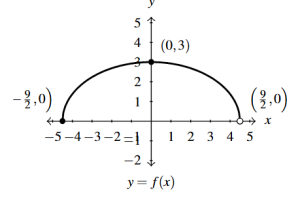
    The rectangular plane with the graph of f(x) horizontally scaled by a factor of 2/3.
    Answer to Exercise 46
  47. [latex]m(x) = -\frac{1}{4}f(3x)[/latex]
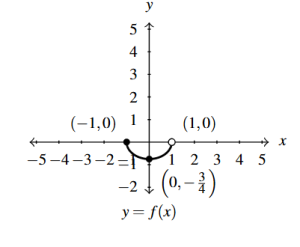
    The rectangular plane with the graph of f(x) horizontally scaled by a factor of 3, vertically scaled by a factor of 1/4, and then reflected over the x-axis.
    Answer to Exercise 47
  48. [latex]n(x) = 4f(x - 3) - 6[/latex]
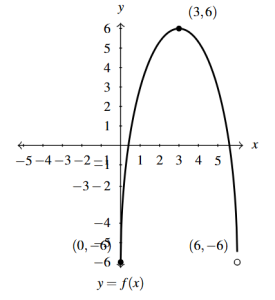
    The rectangular plane with the graph of f(x) shifted right 3 units, vertically scaled by a factor of 4, and then shifted down by 6 units.
    Answer to Exercise 48
  49. [latex]p(x) = 4 + f(1 - 2x) = f(-2x + 1) + 4[/latex]
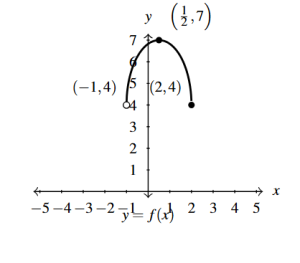
    The rectangular plane with the graph of f(x) shifted left 0.5 units, horizontally scaled by a factor of 2, reflected over the y-axis, and then shifted up 4 units.
    Answer to Exercise 49
  50. [latex]q(x) = -\frac{1}{2}f\left(\frac{x + 4}{2}\right) - 3 = -\frac{1}{2}f\left( \frac{1}{2}x + 2 \right) - 3[/latex]
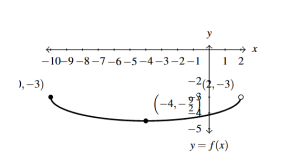
    The rectangular plane with the graph of f(x) shifted left 4 units, horizontally scaled by a factor 1/2, vertically scaled by a factor of 1/2, reflected over the x-axis, and last shifted down 3 units.
    Answer to Exercise 50
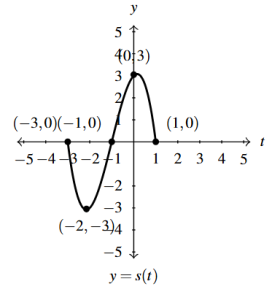
  51. [latex]y = S_{\text{\tiny 1}}(t) = S(t + 1)[/latex]
    The rectangular plane with the graph of S(t) shifted left 1 unit.
    Answer to Exercise 51
  52. [latex]y = S_{\text{\tiny 2}}(t) = S_{\text{\tiny 1}}(-t) = S(-t + 1)[/latex]
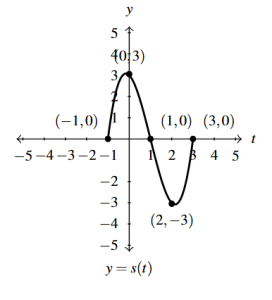
    The rectangular plane with the graph of S(t) shifted left 1 unit and then reflected across the y-axis.
    Answer to Exercise 52
  53. [latex]y = S_{\text{\tiny 3}}(t) = \frac{1}{2} S_{\text{\tiny 2}}(t) = \frac{1}{2}S(-t+1)[/latex]
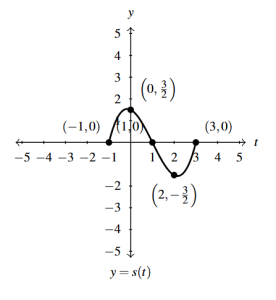
    The rectangular plane with the graph of S(t) shifted left 1 unit, then reflected across the y-axis, and then vertically scaled by a factor of 1/2.
    Answer to Exercise 53
  54. [latex]y = S_{\text{\tiny 4}}(t) = S_{\text{\tiny 3}}(t) + 1 = \frac{1}{2}S(-t+1) + 1[/latex]
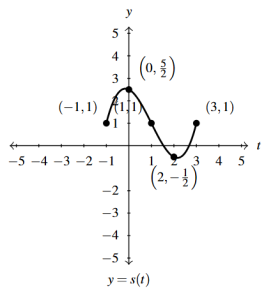
    The rectangular plane with the graph of S(t) shifted left 1 unit, then reflected across the y-axis, vertically scaled by a factor of 1/2, and last shifted up 1 unit.
    Answer to Exercise 54
  55. [latex]g(x) = \sqrt{x-2} - 3[/latex]
  56. [latex]g(x) = \sqrt{x-2} - 3[/latex]
  57. [latex]g(x) = -\sqrt{x} + 1[/latex]
  58. [latex]g(x) = -(\sqrt{x} + 1) = -\sqrt{x} - 1[/latex]
  59. [latex]g(x) = \sqrt{-x+1} + 2[/latex]
  60. [latex]g(x) = \sqrt{-(x+1)} + 2 = \sqrt{-x-1} + 2[/latex]
  61. [latex]g(x) = 2\sqrt{x+3} - 4[/latex]
  62. [latex]g(x) = 2\left(\sqrt{x+3} - 4\right) = 2\sqrt{x+3} - 8[/latex]
  63. [latex]g(x) = \sqrt{2x-3} + 1[/latex]
  64. [latex]g(x) = \sqrt{2(x-3)} + 1 = \sqrt{2x-6}+1[/latex]
  65. [latex]g(x)=f(x)+1[/latex]
  66. [latex]h(x) = f(x-2)[/latex]
  67. [latex]p(x) = f\left( \frac{x}{2} \right) -1[/latex]
  68. [latex]q(x) = -2f(x) = 2f(-x)[/latex]
  69. [latex]r(x) = 2f(x+1)-3[/latex]
  70. [latex]s(x) = 2f(-x+1)-3 = -2f(x-1)+3[/latex]
  71. [latex]g(x) = -2\sqrt[3]{x + 3} - 1[/latex] or [latex]g(x) = 2\sqrt[3]{-x - 3} - 1[/latex]
  72. Answers May Vary
  73. Answers May Vary
  74. Answers May Vary
  75. Answers May Vary
  76. Answers May Vary

 

  1. This is called the fixed or start-up cost. We'll revisit this concept in Example 1.3.8 in Section 1.3.1. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Functions, Trigonometry, and Systems of Equations (Second Edition) Copyright © 2025 by Texas A&M Mathematics Department is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book