Section 7.1 Answers
- [latex]30^{\circ}[/latex] is a Quadrant I angle
coterminal with [latex]390^{\circ}[/latex] and [latex]-330^{\circ}[/latex]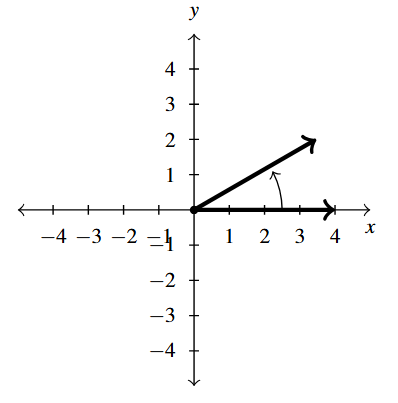
Answer to Exercise 1 - [latex]120^{\circ}[/latex] is a Quadrant II angle
coterminal with [latex]480^{\circ}[/latex] and [latex]-240^{\circ}[/latex]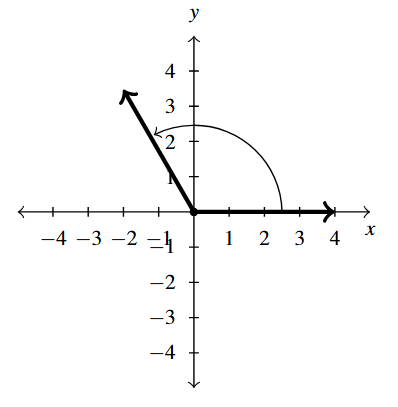
Answer to Exercise 2 - [latex]225^{\circ}[/latex] is a Quadrant III angle
coterminal with [latex]585^{\circ}[/latex] and [latex]-135^{\circ}[/latex]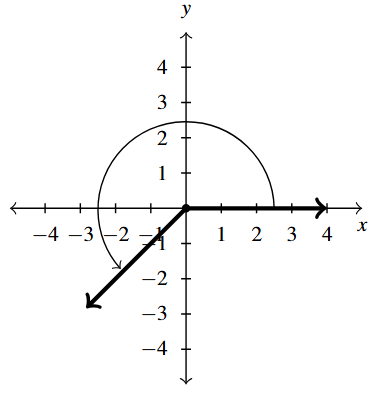
Answer to Exercise 3 - [latex]330^{\circ}[/latex] is a Quadrant IV angle
coterminal with [latex]690^{\circ}[/latex] and [latex]-30^{\circ}[/latex]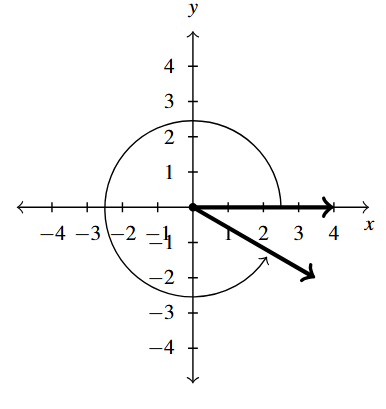
Answer to Exercise 4 - [latex]-30^{\circ}[/latex] is a Quadrant IV angle
coterminal with [latex]330^{\circ}[/latex] and [latex]-390^{\circ}[/latex]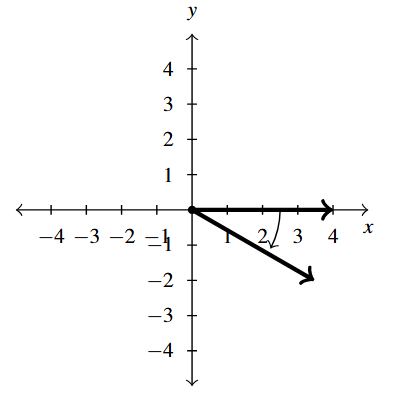
Answer to Exercise 5 - [latex]-135^{\circ}[/latex] is a Quadrant III angle
coterminal with [latex]225^{\circ}[/latex] and [latex]-495^{\circ}[/latex]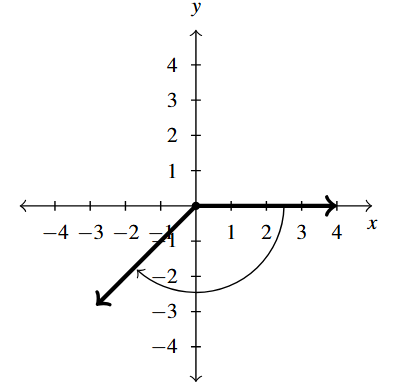
Answer to Exercise 6 - [latex]-240^{\circ}[/latex] is a Quadrant II angle
coterminal with [latex]120^{\circ}[/latex] and [latex]-600^{\circ}[/latex]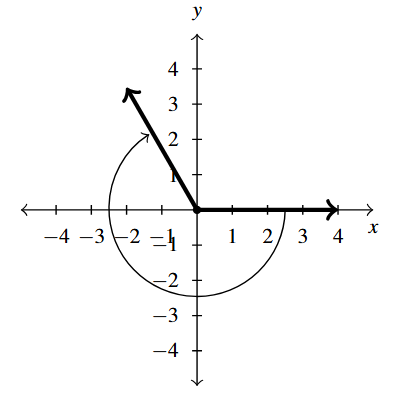
Answer to Exercise 7 - [latex]-270^{\circ}[/latex] is a quadrantal angle
coterminal with [latex]90^{\circ}[/latex] and [latex]-630^{\circ}[/latex]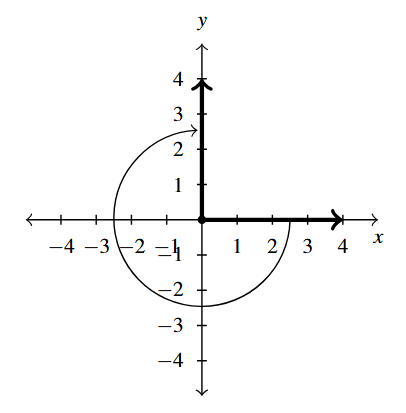
Answer to Exercise 8 - [latex]405^{\circ}[/latex] is a Quadrant I angle
coterminal with [latex]45^{\circ}[/latex] and [latex]-315^{\circ}[/latex]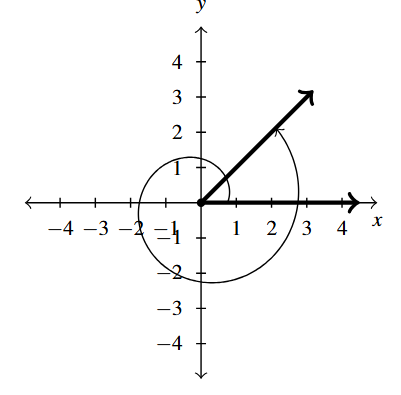
Answer to Exercise 9 - [latex]840^{\circ}[/latex] is a Quadrant II angle
coterminal with [latex]120^{\circ}[/latex] and [latex]-240^{\circ}[/latex]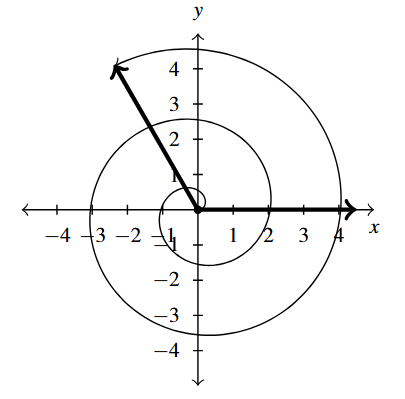
Answer to Exercise 10 - [latex]-510^{\circ}[/latex] is a Quadrant III angle
coterminal with [latex]-150^{\circ}[/latex] and [latex]210^{\circ}[/latex]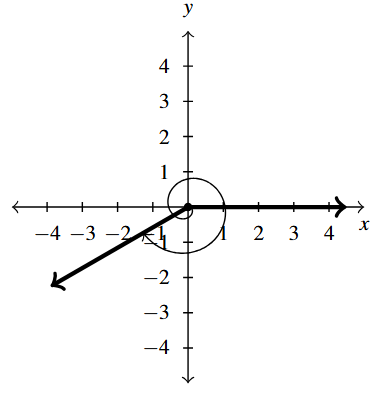
Answer to Exercise 11 - [latex]-900^{\circ}[/latex] is a quadrantal angle
coterminal with [latex]-180^{\circ}[/latex] and [latex]180^{\circ}[/latex]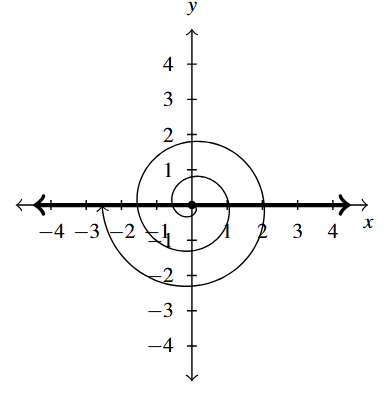
Answer to Exercise 12 - [latex]\dfrac{\pi}{3}[/latex] is a Quadrant I angle
coterminal with [latex]\dfrac{7\pi}{3}[/latex] and [latex]-\dfrac{5\pi}{3}[/latex]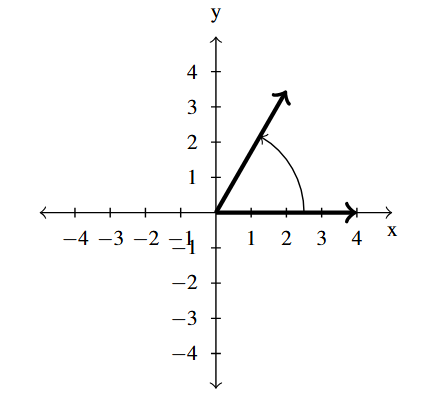
Answer to Exercise 13 - [latex]\dfrac{5\pi}{6}[/latex] is a Quadrant II angle
coterminal with [latex]\dfrac{17\pi}{6}[/latex] and [latex]-\dfrac{7\pi}{6}[/latex]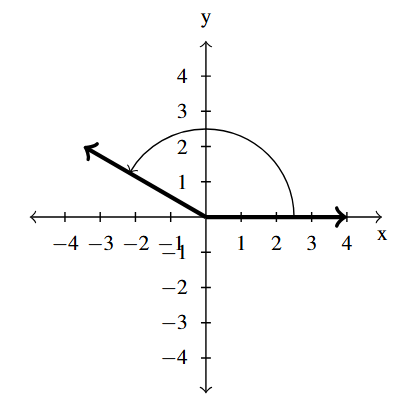
Answer to Exercise 14 - [latex]-\dfrac{11\pi}{3}[/latex] is a Quadrant I angle
coterminal with [latex]\dfrac{\pi}{3}[/latex] and [latex]-\dfrac{5\pi}{3}[/latex]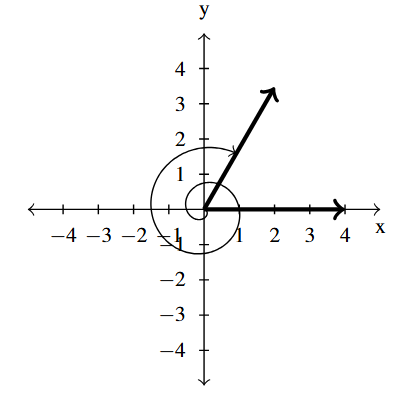
Answer to Exercise 15 - [latex]\dfrac{5\pi}{4}[/latex] is a Quadrant III angle
coterminal with [latex]\dfrac{13\pi}{4}[/latex] and [latex]-\dfrac{3\pi}{4}[/latex]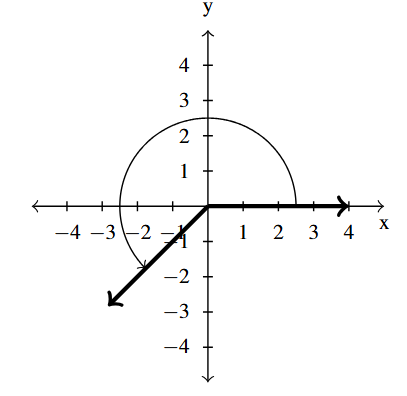
Answer to Exercise 16 - [latex]\dfrac{3\pi}{4}[/latex] is a Quadrant II angle
coterminal with [latex]\dfrac{11\pi}{4}[/latex] and [latex]-\dfrac{5\pi}{4}[/latex]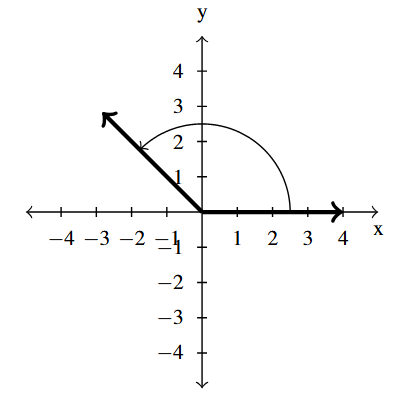
Answer to Exercise 17 - [latex]-\dfrac{\pi}{3}[/latex] is a Quadrant IV angle
coterminal with [latex]\dfrac{5\pi}{3}[/latex] and [latex]-\dfrac{7\pi}{3}[/latex]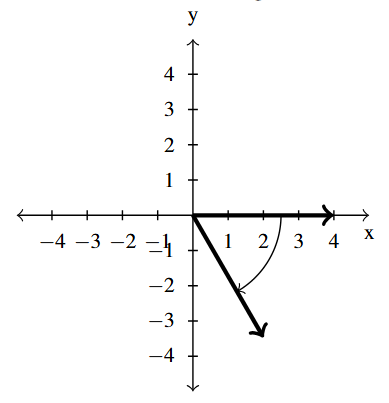
Answer to Exercise 18 - [latex]\dfrac{7\pi}{2}[/latex] lies on the negative [latex]y[/latex]-axis
coterminal with [latex]\dfrac{3\pi}{2}[/latex] and [latex]-\dfrac{\pi}{2}[/latex]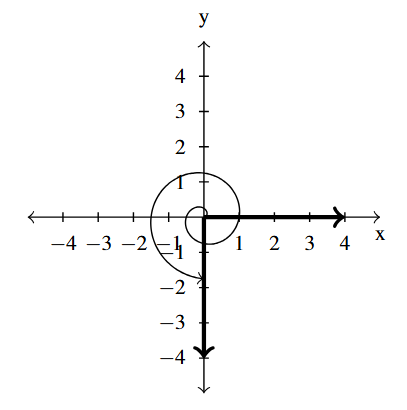
Answer to Exercise 19 - [latex]\dfrac{\pi}{4}[/latex] is a Quadrant I angle
coterminal with [latex]\dfrac{9 \pi}{4}[/latex] and [latex]-\dfrac{7\pi}{4}[/latex]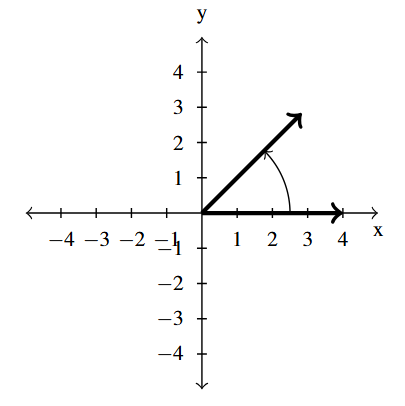
Answer to Exercise 20 - [latex]-\dfrac{\pi}{2}[/latex] lies on the negative [latex]y[/latex]-axis
coterminal with [latex]\dfrac{3\pi}{2}[/latex] and [latex]-\dfrac{5\pi}{2}[/latex]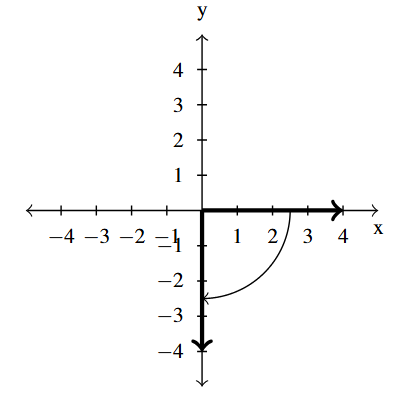
Answer to Exercise 21 - [latex]\dfrac{7\pi}{6}[/latex] is a Quadrant III angle
coterminal with [latex]\dfrac{19 \pi}{6}[/latex] and [latex]-\dfrac{5\pi}{6}[/latex]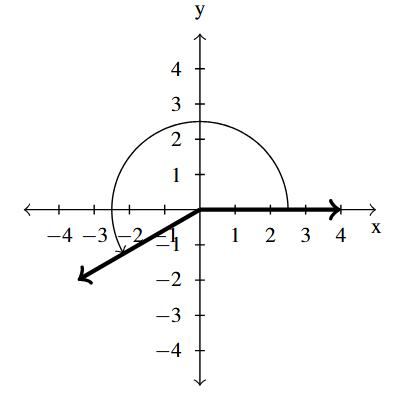
Answer to Exercise 22 - [latex]-\dfrac{5\pi}{3}[/latex] is a Quadrant I angle
coterminal with [latex]\dfrac{\pi}{3}[/latex] and [latex]-\dfrac{11\pi}{3}[/latex]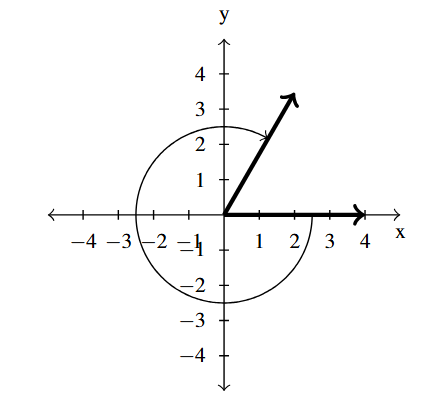
Answer to Exercise 23 - [latex]3\pi[/latex] lies on the negative [latex]x[/latex]-axis
coterminal with [latex]\pi[/latex] and [latex]-\pi[/latex]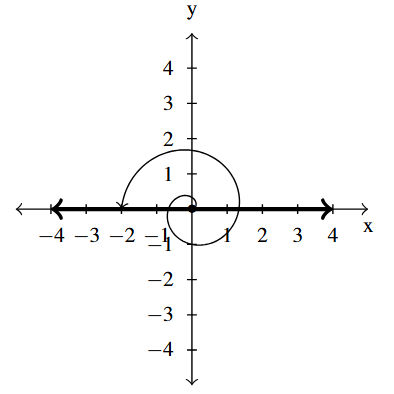
Answer to Exercise 24 - [latex]-2\pi[/latex] lies on the positive [latex]x[/latex]-axis
coterminal with [latex]2\pi[/latex] and [latex]-4\pi[/latex]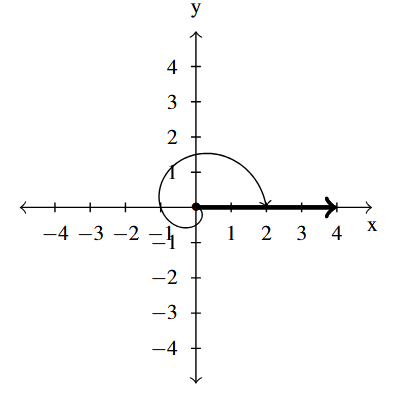
Answer to Exercise 25 - [latex]-\dfrac{\pi}{4}[/latex] is a Quadrant IV angle
coterminal with [latex]\dfrac{7 \pi}{4}[/latex] and [latex]-\dfrac{9\pi}{4}[/latex]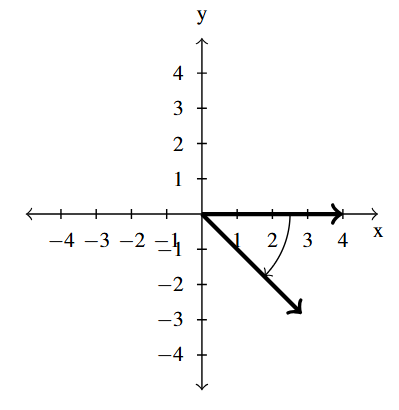
Answer to Exercise 26 - [latex]-\dfrac{\pi}{4}[/latex] is a Quadrant IV angle
coterminal with [latex]\dfrac{7 \pi}{4}[/latex] and [latex]-\dfrac{9\pi}{4}[/latex]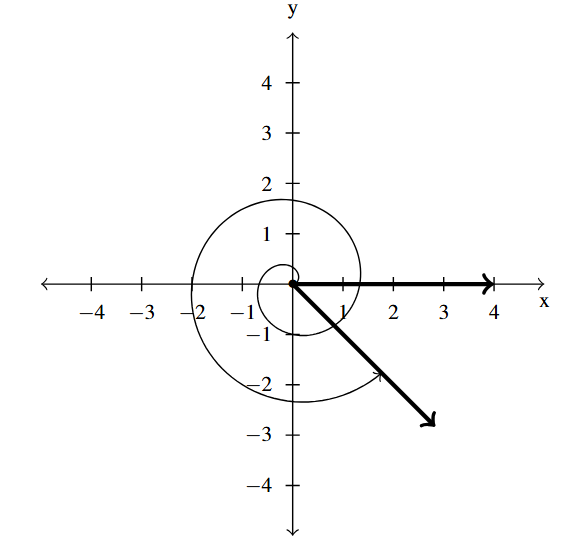
Answer to Exercise 27 - [latex]-\dfrac{13\pi}{6}[/latex] is a Quadrant IV angle
coterminal with [latex]\dfrac{11\pi}{6}[/latex] and [latex]-\dfrac{\pi}{6}[/latex]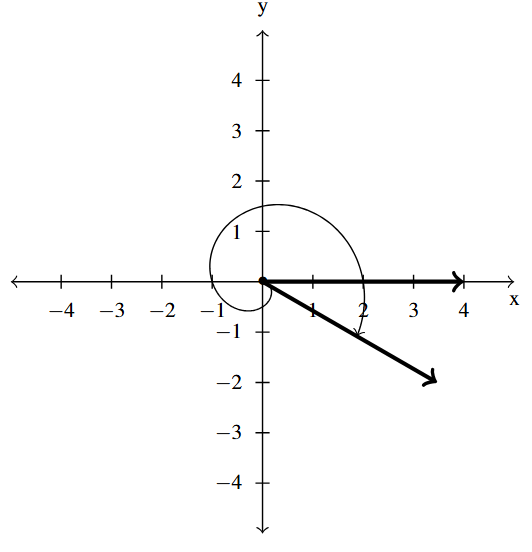
Answer to Exercise 28 - 0
- [latex]\dfrac{4\pi}{3}[/latex]
- [latex]\dfrac{3\pi}{4}[/latex]
- [latex]-\dfrac{3\pi}{2}[/latex]
- [latex]-\dfrac{7\pi}{4}[/latex]
- [latex]\dfrac{5\pi}{6}[/latex]
- [latex]\dfrac{\pi}{4}[/latex]
- [latex]-\dfrac{5\pi}{4}[/latex]
- [latex]180^{\circ}[/latex]
- [latex]-120^{\circ}[/latex]
- [latex]210^{\circ}[/latex]
- [latex]330^{\circ}[/latex]
- [latex]60^{\circ}[/latex]
- [latex]300^{\circ}[/latex]
- [latex]-30^{\circ}[/latex]
- [latex]90^{\circ}[/latex]
- [latex]t = \dfrac{5\pi}{6}[/latex]
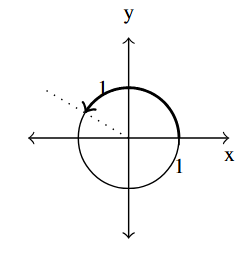
Answer to Exercise 45 - [latex]t = -\pi[/latex]
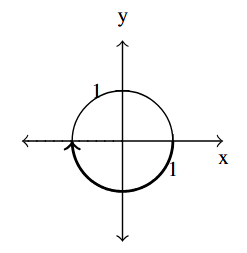
Answer to Exercise 46 - [latex]t = 6[/latex]
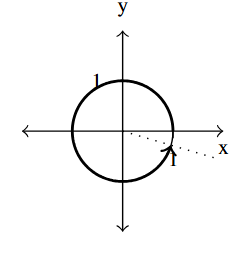
Answer to Exercise 47 - [latex]t = -2[/latex]
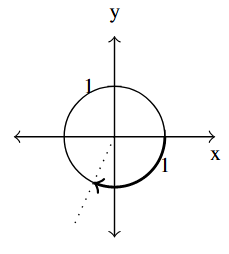
Answer to Exercise 48 - [latex]t = 12[/latex] (between 1 and 2 revolutions)
Answer to Exercise 49 - [latex]\dfrac{3375 \pi}{352}[/latex] miles per hour
- [latex]\dfrac{19712}{\pi}[/latex] revolutions per minute
- [latex]\dfrac{35 \pi}{33}[/latex] miles per hour
- [latex]\dfrac{375 \pi}{22}[/latex] miles per hour
- 70 miles per hour
- [latex]\dfrac{1920 \pi}{1397}[/latex] miles per hour
- Answers May Vary
- [latex]12\pi[/latex] square units
- [latex]6250\pi[/latex] square units
- [latex]79.2825\pi \approx 249.07[/latex] square units
- [latex]\dfrac{\pi}{2}[/latex] square units
- [latex]\dfrac{50\pi}{3}[/latex] square units
- [latex]38.025 \pi \approx 119.46[/latex] square units
Section 7.2 Answers
- [latex]\theta = 30^{\circ}[/latex], [latex]a = 3\sqrt{3}[/latex], [latex]c = \sqrt{108} = 6\sqrt{3}[/latex]
- [latex]\alpha = 56^{\circ}[/latex], [latex]b = 12 \tan(34^{\circ}) = 8.094[/latex], [latex]c = 12\sec(34^{\circ}) = \dfrac{12}{\cos(34^{\circ})} \approx 14.475[/latex]
- [latex]\theta = 43^{\circ}[/latex], [latex]a = 6\cot(47^{\circ}) = \dfrac{6}{\tan(47^{\circ})} \approx 5.595[/latex], [latex]c = 6\csc(47^{\circ}) = \dfrac{6}{\sin(47^{\circ})} \approx 8.204[/latex]
- [latex]\beta = 40^{\circ}[/latex], [latex]b = 2.5 \tan(50^{\circ}) \approx 2.979[/latex], [latex]c = 2.5\sec(50^{\circ}) = \dfrac{2.5}{\cos(50^{\circ})} \approx 3.889[/latex]
- The side opposite [latex]\theta[/latex] has length [latex]10 \sin(15^{\circ}) \approx 2.588[/latex]
-
The hypoteneuse has length [latex]14 \csc(38.2^{\circ}) = \dfrac{14}{\sin(38.2^{\circ})} \approx 22.639[/latex]
-
The side adjacent to [latex]\theta[/latex] has length [latex]3.98 \cos(2.05^{\circ}) \approx 3.977[/latex]
- [latex]\cos(0) = 1[/latex], [latex]\; \sin(0) = 0[/latex]
- [latex]\cos \left(\dfrac{\pi}{4} \right) = \dfrac{\sqrt{2}}{2}[/latex], [latex]\; \sin \left(\dfrac{\pi}{4} \right) = \dfrac{\sqrt{2}}{2}[/latex]
- [latex]\cos \left(\dfrac{\pi}{3}\right) = \dfrac{1}{2}[/latex], [latex]\; \sin \left(\dfrac{\pi}{3}\right) = \dfrac{\sqrt{3}}{2}[/latex]
- [latex]\cos \left(\dfrac{\pi}{2}\right) = 0[/latex], [latex]\; \sin \left(\dfrac{\pi}{2}\right) = 1[/latex]
- [latex]\cos\left(\dfrac{2\pi}{3}\right) = -\dfrac{1}{2}[/latex], [latex]\; \sin \left(\dfrac{2\pi}{3}\right) = \dfrac{\sqrt{3}}{2}[/latex]
- [latex]\cos \left(\dfrac{3\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}[/latex], [latex]\; \sin \left(\dfrac{3\pi}{4} \right) = \dfrac{\sqrt{2}}{2}[/latex]
- [latex]\cos(\pi) = -1[/latex], [latex]\; \sin(\pi) = 0[/latex]
- [latex]\cos\left(\dfrac{7\pi}{6}\right) = -\dfrac{\sqrt{3}}{2}[/latex], [latex]\; \sin\left(\dfrac{7\pi}{6}\right) = -\dfrac{1}{2}[/latex]
- [latex]\cos \left(\dfrac{5\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}[/latex], [latex]\; \sin \left(\dfrac{5\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}[/latex]
- [latex]\cos\left(\dfrac{4\pi}{3}\right) = -\dfrac{1}{2}[/latex], [latex]\; \sin \left(\dfrac{4\pi}{3}\right) = -\dfrac{\sqrt{3}}{2}[/latex]
- [latex]\cos \left(\dfrac{3\pi}{2}\right) = 0[/latex], [latex]\; \sin \left(\dfrac{3\pi}{2}\right) = -1[/latex]
- [latex]\cos\left(\dfrac{5\pi}{3}\right) = \dfrac{1}{2}[/latex], [latex]\; \sin \left(\dfrac{5\pi}{3}\right) = -\dfrac{\sqrt{3}}{2}[/latex]
- [latex]\cos \left(\dfrac{7\pi}{4} \right) = \dfrac{\sqrt{2}}{2}[/latex], [latex]\; \sin \left(\dfrac{7\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}[/latex]
- [latex]\cos\left(\dfrac{23\pi}{6}\right) = \dfrac{\sqrt{3}}{2}[/latex], [latex]\; \sin\left(\dfrac{23\pi}{6}\right) = -\dfrac{1}{2}[/latex]
- [latex]\cos \left(-\dfrac{13\pi}{2}\right) = 0[/latex], [latex]\; \sin \left(-\dfrac{13\pi}{2}\right) = -1[/latex]
- [latex]\cos\left(-\dfrac{43\pi}{6}\right) = -\dfrac{\sqrt{3}}{2}[/latex], [latex]\; \sin\left(-\dfrac{43\pi}{6}\right) = \dfrac{1}{2}[/latex]
- [latex]\cos \left(-\dfrac{3\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}[/latex], [latex]\; \sin \left(-\dfrac{3\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}[/latex]
- [latex]\cos\left(-\dfrac{\pi}{6}\right) = \dfrac{\sqrt{3}}{2}[/latex], [latex]\; \sin\left(-\dfrac{\pi}{6}\right) = -\dfrac{1}{2}[/latex]
- [latex]\cos\left(\dfrac{10\pi}{3}\right) = -\dfrac{1}{2}[/latex], [latex]\; \sin \left(\dfrac{10\pi}{3}\right) = -\dfrac{\sqrt{3}}{2}[/latex]
- [latex]\cos(117\pi) = -1[/latex], [latex]\; \sin(117\pi) = 0[/latex]
- [latex]\sin(\theta) = \dfrac{1}{2}[/latex] when [latex]\theta = \dfrac{\pi}{6} + 2\pi k[/latex] or [latex]\theta = \dfrac{5\pi}{6} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cos(\theta) = -\dfrac{\sqrt{3}}{2}[/latex] when [latex]\theta = \dfrac{5\pi}{6} + 2\pi k[/latex] or [latex]\theta = \dfrac{7\pi}{6} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\sin(\theta) = 0[/latex] when [latex]\theta = \pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cos(\theta) = \dfrac{\sqrt{2}}{2}[/latex] when [latex]\theta = \dfrac{\pi}{4} + 2\pi k[/latex] or [latex]\theta = \dfrac{7\pi}{4} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\sin(\theta) = \dfrac{\sqrt{3}}{2}[/latex] when [latex]\theta = \dfrac{\pi}{3} + 2\pi k[/latex] or [latex]\theta = \dfrac{2\pi}{3} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cos(\theta) = -1[/latex] when [latex]\theta = (2k + 1)\pi[/latex] for any integer [latex]k[/latex].
- [latex]\sin(\theta) = -1[/latex] when [latex]\theta = \dfrac{3\pi}{2} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cos(\theta) = \dfrac{\sqrt{3}}{2}[/latex] when [latex]\theta = \dfrac{\pi}{6} + 2\pi k[/latex] or [latex]\theta = \dfrac{11\pi}{6} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cos(\theta) = -1.001[/latex] never happens
- [latex]\cos(t) = 0[/latex] when [latex]t = \dfrac{\pi}{2} + \pi k[/latex] for any integer [latex]k[/latex].
- [latex]\sin(t) = -\dfrac{\sqrt{2}}{2}[/latex] when [latex]t = \dfrac{5\pi}{4} + 2\pi k[/latex] or [latex]t = \dfrac{7\pi}{4} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cos(t) = 3[/latex] never happens.
- [latex]\sin(t) = -\dfrac{1}{2}[/latex] when [latex]t = \dfrac{7\pi}{6} + 2\pi k[/latex] or [latex]t = \dfrac{11\pi}{6} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cos(t) = \dfrac{1}{2}[/latex] when [latex]t = \dfrac{\pi}{3} + 2\pi k[/latex] or [latex]t = \dfrac{5\pi}{3} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\sin(t) = -2[/latex] never happens
- [latex]\cos(t) = 1[/latex] when [latex]t = 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\sin(t) = 1[/latex] when [latex]t = \dfrac{\pi}{2} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cos(t) = -\dfrac{\sqrt{2}}{2}[/latex] when [latex]t = \dfrac{3\pi}{4} + 2\pi k[/latex] or [latex]t = \dfrac{5\pi}{4} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cos(\theta) = -\dfrac{7}{25}, \; \sin(\theta) = \dfrac{24}{25}[/latex]
- [latex]\cos(\theta) = \dfrac{3}{5}, \; \sin(\theta) = \dfrac{4}{5}[/latex]
- [latex]\cos(\theta) = \dfrac{5\sqrt{106}}{106}, \; \sin(\theta) = -\dfrac{9\sqrt{106}}{106}[/latex]
- [latex]\cos(\theta) = -\dfrac{2\sqrt{5}}{25}, \; \sin(\theta) = -\dfrac{11\sqrt{5}}{25}[/latex]
- If [latex]\sin(\theta) = -\dfrac{7}{25}[/latex] with [latex]\theta[/latex] in Quadrant IV, then [latex]\cos(\theta) = \dfrac{24}{25}[/latex].
- If [latex]\cos(\theta) = \dfrac{4}{9}[/latex] with [latex]\theta[/latex] in Quadrant I, then [latex]\sin(\theta) = \dfrac{\sqrt{65}}{9}[/latex].
- If [latex]\sin(\theta) = \dfrac{5}{13}[/latex] with [latex]\theta[/latex] in Quadrant II, then [latex]\cos(\theta) = -\dfrac{12}{13}[/latex].
- If [latex]\cos(\theta) = -\dfrac{2}{11}[/latex] with [latex]\theta[/latex] in Quadrant III, then [latex]\sin(\theta) = -\dfrac{\sqrt{117}}{11}[/latex].
- If [latex]\sin(\theta) = -\dfrac{2}{3}[/latex] with [latex]\theta[/latex] in Quadrant III, then [latex]\cos(\theta) = -\dfrac{\sqrt{5}}{3}[/latex].
- If [latex]\cos(\theta) = \dfrac{28}{53}[/latex] with [latex]\theta[/latex] in Quadrant IV, then [latex]\sin(\theta) = -\dfrac{45}{53}[/latex].
- If [latex]\sin(\theta) = \dfrac{2\sqrt{5}}{5}[/latex] and [latex]\dfrac{\pi}{2}[/latex] < [latex]\theta[/latex] < [latex]\pi[/latex], then [latex]\cos(\theta) = -\dfrac{\sqrt{5}}{5}[/latex].
- If [latex]\cos(\theta) = \dfrac{\sqrt{10}}{10}[/latex] and [latex]2\pi[/latex] < [latex]\theta[/latex] < [latex]\dfrac{5\pi}{2}[/latex], then [latex]\sin(\theta) = \dfrac{3 \sqrt{10}}{10}[/latex].
- If [latex]\sin(\theta) = -0.42[/latex] and [latex]\pi[/latex] < [latex]\theta[/latex] < [latex]\dfrac{3\pi}{2}[/latex], then [latex]\cos(\theta) = -\sqrt{0.8236} \approx -0.9075[/latex].
- If [latex]\cos(\theta) = -0.98[/latex] and [latex]\dfrac{\pi}{2}[/latex] < [latex]\theta[/latex] < [latex]\pi[/latex], then [latex]\sin(\theta) = \sqrt{0.0396} \approx 0.1990[/latex].
- One solution is [latex]g(t) = 3t[/latex] and [latex]h(t) = \sin(2t)[/latex].
- One solution is [latex]g(\theta) = 3 \cos(\theta)[/latex] and [latex]h(\theta) = \sin(4 \theta)[/latex].
- One solution is [latex]g(t) = e^{-0.1t}[/latex] and [latex]h(t) = \sin(3t)[/latex].
- One solution is [latex]f(t) = \sin(t)[/latex] and [latex]g(t) = t[/latex].
- One solution is [latex]f(\theta) = 3 \cos(\theta)[/latex] and [latex]g(\theta) = \sqrt{\theta}[/latex].
- As we zoom in towards 0, the average rate of change of [latex]\sin(k t)[/latex] approaches [latex]k[/latex].
![A table with five rows and four columns. The first row is the header row with S(t), [-0.1, 0.1], [-0.01, 0.01], and [-0.001, 0.001]. The first column has the functions sine of t, sine of 2t, sine of 3t, and sine of 4t. The remaining entries are the values of the functions over the intervals.](https://odp.library.tamu.edu/app/uploads/sites/96/2025/06/Answer_7_2_65.png)
Answer to Exercise 65 -
[latex]r = 1.125[/latex] inches, [latex]\omega = 9000 \pi \, \frac{\text{radians}}{\text{minute}}[/latex], [latex]x = 1.125 \cos(9000 \pi \, t)[/latex], [latex]y = 1.125 \sin(9000 \pi \, t)[/latex]. Here [latex]x[/latex] and [latex]y[/latex] are measured in inches and [latex]t[/latex] is measured in minutes.
-
[latex]r = 28[/latex] inches, [latex]\omega = \frac{2\pi}{3} \, \frac{\text{radians}}{\text{second}}[/latex], [latex]x = 28 \cos\left(\frac{2\pi}{3} \, t \right)[/latex], [latex]y = 28 \sin\left(\frac{2\pi}{3} \, t \right)[/latex]. Here [latex]x[/latex] and [latex]y[/latex] are measured in inches and [latex]t[/latex] is measured in seconds.
-
[latex]r = 1.25[/latex] inches, [latex]\omega = 14400 \pi \, \frac{\text{radians}}{\text{minute}}[/latex], [latex]x = 1.25 \cos(14400 \pi \, t)[/latex], [latex]y = 1.25 \sin(14400 \pi \, t)[/latex]. Here [latex]x[/latex] and [latex]y[/latex] are measured in inches and [latex]t[/latex] is measured in minutes.
-
[latex]r = 64[/latex] feet, [latex]\omega = \frac{4\pi}{127} \, \frac{\text{radians}}{\text{second}}[/latex], [latex]x = 64 \cos\left(\frac{4\pi}{127} \, t \right)[/latex], [latex]y = 64 \sin\left(\frac{4\pi}{127} \, t \right)[/latex]. Here [latex]x[/latex] and [latex]y[/latex] are measured in feet and [latex]t[/latex] is
Section 7.3 Answers
- [latex]f(t) = 3\sin(t)[/latex]
Period: [latex]2\pi[/latex]
Amplitude: 3
Phase Shift: 0
Vertical Shift: 0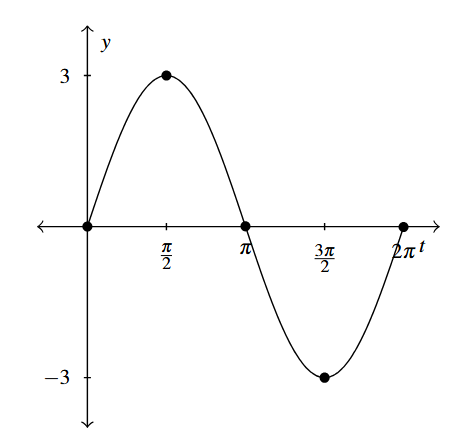
Answer to Exercise 1 - [latex]g(t) = \sin(3t)[/latex]
Period: [latex]\frac{2\pi}{3}[/latex]
Amplitude: 1
Phase Shift: 0
Vertical Shift: 0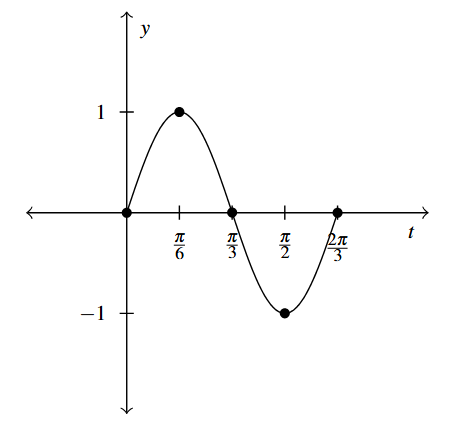
Answer to Exercise 2 - [latex]h(t) = -2\cos(t)[/latex]
Period: [latex]2\pi[/latex]
Amplitude: 2
Phase Shift: 0
Vertical Shift: 0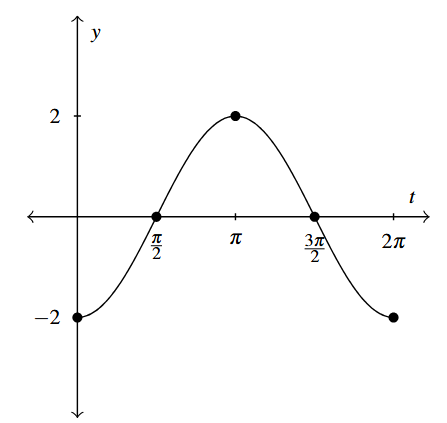
Answer to Exercise 3 - [latex]f(t) = \cos \left( t - \frac{\pi}{2} \right)[/latex]
Period: [latex]2\pi[/latex]
Amplitude: 1
Phase Shift: [latex]\frac{\pi}{2}[/latex]
Vertical Shift: 0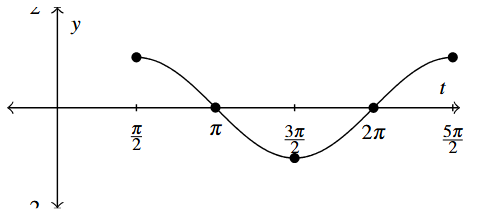
Answer to Exercise 4 - [latex]g(t) = -\sin \left( t + \frac{\pi}{3} \right)[/latex]
Period: [latex]2\pi[/latex]
Amplitude: 1
Phase Shift: [latex]-\frac{\pi}{3}[/latex]
Vertical Shift: 0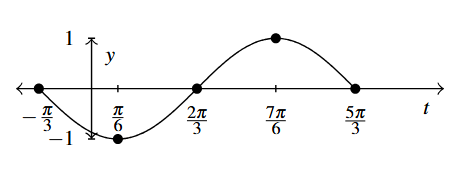
Answer to Exercise 5 - [latex]h(t) = \sin(2t - \pi)[/latex]
Period: [latex]\pi[/latex]
Amplitude: 1
Phase Shift: [latex]\frac{\pi}{2}[/latex]
Vertical Shift: 0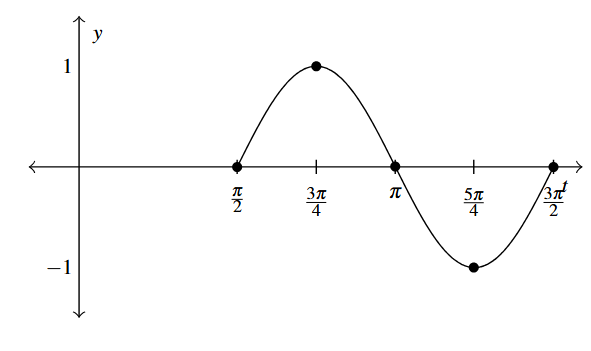
Answer to Exercise 6 - [latex]f(t) = -\frac{1}{3}\cos \left( \frac{1}{2}t + \frac{\pi}{3} \right)[/latex]
Period: [latex]4\pi[/latex]
Amplitude: [latex]\frac{1}{3}[/latex]
Phase Shift: [latex]-\frac{2\pi}{3}[/latex]
Vertical Shift: 0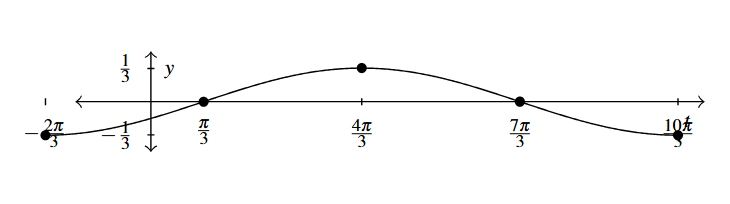
Answer to Exercise 7 - [latex]g(t) = \cos (3t - 2\pi) + 4[/latex]
Period: [latex]\frac{2\pi}{3}[/latex]
Amplitude: 1
Phase Shift: [latex]\frac{2\pi}{3}[/latex]
Vertical Shift: 4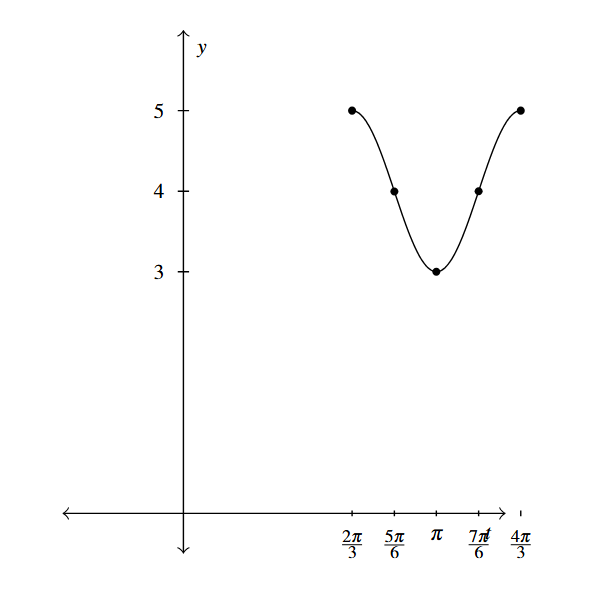
Answer to Exercise 8 - [latex]h(t) = \sin \left( -t - \frac{\pi}{4} \right) - 2[/latex]
Period: [latex]2\pi[/latex]
Amplitude: 1
Phase Shift: [latex]-\frac{\pi}{4}[/latex] (You need to use [latex]y = -\sin \left( t + \frac{\pi}{4} \right) - 2[/latex] to find this.)[1]
Vertical Shift: [latex]-2[/latex]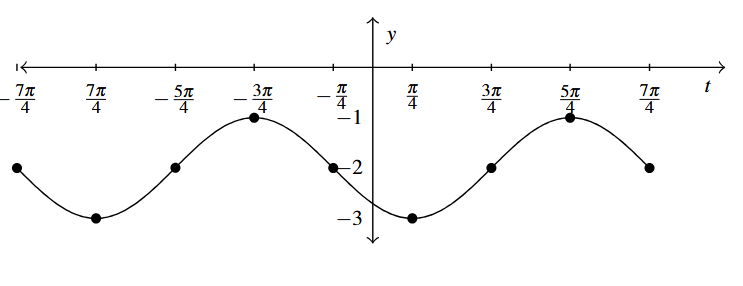
Answer to Exercise 9 - [latex]f(t) = \frac{2}{3} \cos \left( \frac{\pi}{2} - 4t \right) + 1[/latex]
Period: [latex]\frac{\pi}{2}[/latex]
Amplitude: [latex]\frac{2}{3}[/latex]
Phase Shift: [latex]\frac{\pi}{8}[/latex] (You need to use [latex]y = \frac{2}{3} \cos \left( 4t - \frac{\pi}{2} \right) + 1[/latex] to find this.)[2]
Vertical Shift: 1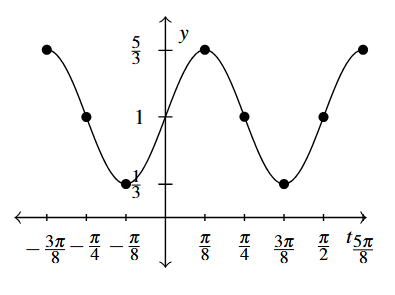
Answer to Exercise 10 - [latex]g(t) = -\frac{3}{2} \cos \left( 2t + \frac{\pi}{3} \right) - \frac{1}{2}[/latex]
Period: [latex]\pi[/latex]
Amplitude: [latex]\frac{3}{2}[/latex]
Phase Shift: [latex]-\frac{\pi}{6}[/latex]
Vertical Shift: [latex]-\frac{1}{2}[/latex]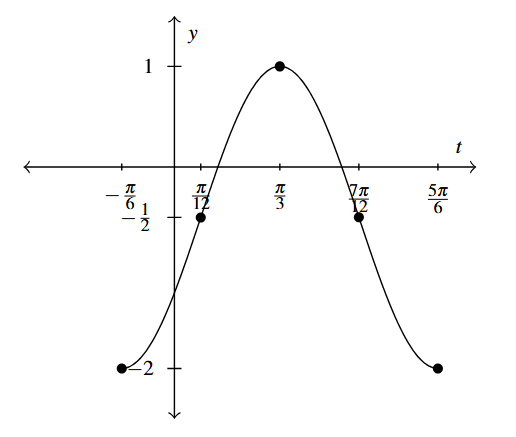
Answer to Exercise 11 - [latex]h(t) = 4\sin (-2\pi t + \pi)[/latex]
Period: 1
Amplitude: 4
Phase Shift: [latex]\frac{1}{2}[/latex] (You need to use [latex]h(t) = -4\sin (2\pi t - \pi)[/latex] to find this.)[3]
Vertical Shift: 0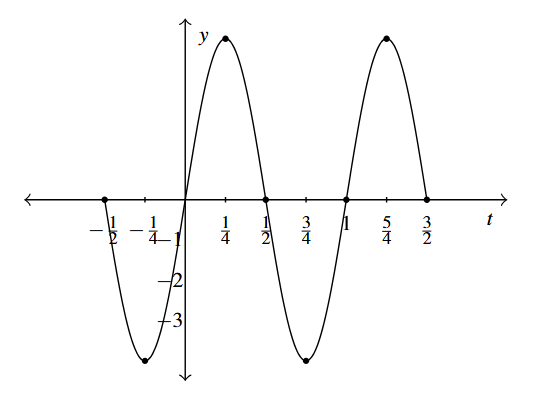
Answer to Exercise 12 - [latex]S(t) = 4 \sin \left(t + \frac{\pi}{4} \right)[/latex], [latex]C(t) = 4 \cos \left(t - \frac{\pi}{4} \right)[/latex]
- [latex]S(t) = -3 \sin(t) + 3[/latex], [latex]C(t) = -3 \cos\left(t - \frac{\pi}{2}\right) + 3[/latex]
- [latex]S(t) = 3 \sin \left( 2t - \frac{\pi}{3} \right)[/latex], [latex]C(t) = 3 \cos \left( 2t - \frac{5\pi}{6} \right)[/latex]
- [latex]S(t) = \frac{7}{2} \sin(\pi t) + \frac{1}{2}[/latex], [latex]C(t) = \frac{7}{2} \cos\left(\pi t \frac{\pi}{2} \right) + \frac{1}{2}[/latex]
-
.
-
[latex]y = |4 \sin(t)|[/latex]. Period: [latex]\pi[/latex].
Two cycles are graphed below.
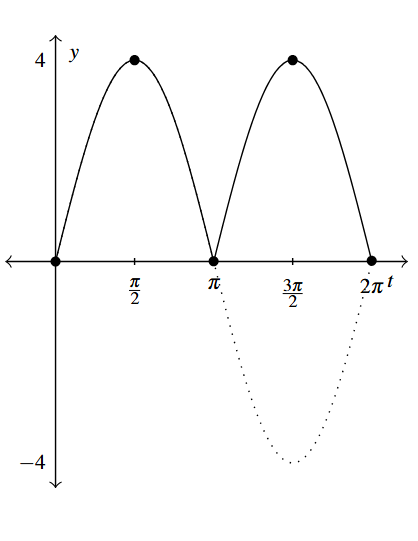
Answer to Exercise 17a -
[latex]y = \sqrt{4 \sin(t)}[/latex]. Period: [latex]2\pi[/latex].
One cycle is graphed below.
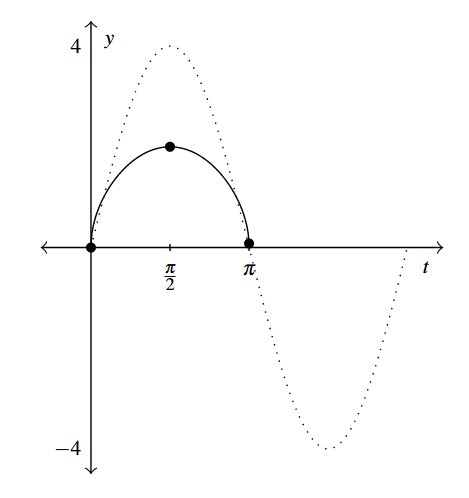
Answer to Exercise 17b
-
- [latex]f(t)=\cos(3t) + \sin(t)[/latex] over [latex][-2\pi, 2\pi][/latex]
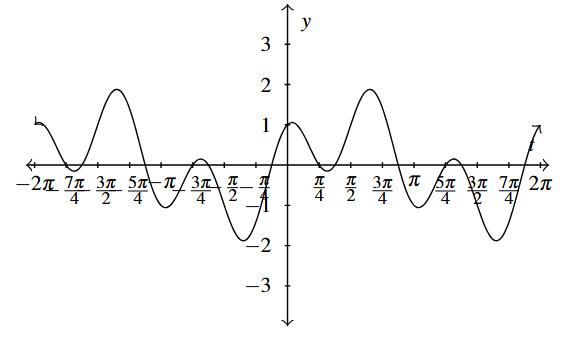
Answer to Exercise 18 - [latex]f(t)=\frac{\sin(t)}{t}[/latex] over [latex][-2\pi, 2\pi][/latex]
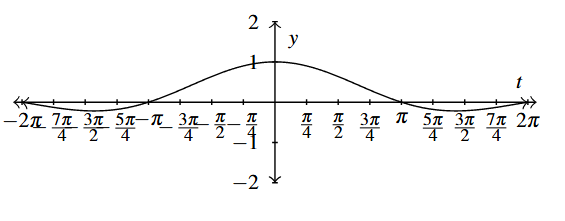
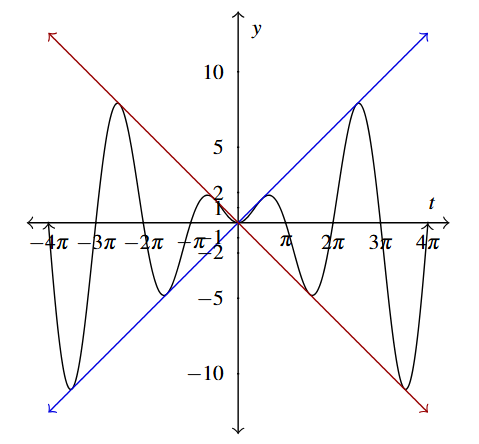
Answer to Exercise 19 - [latex]f(t)=t\sin(t)[/latex] over [latex][-4\pi, 4\pi][/latex]
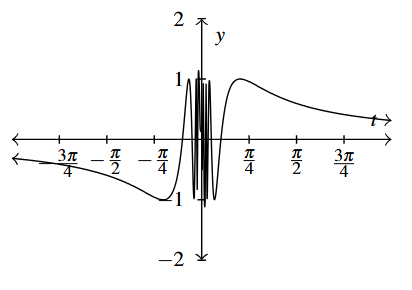
Answer to Exercise 20 - [latex]f(t)=\sin\left(\frac{1}{t}\right)[/latex] over [latex][-\pi, \pi][/latex]
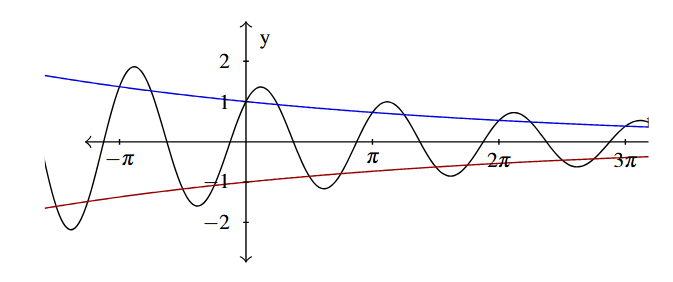
Answer to Exercise 21 - [latex]f(t)=e^{-0.1t}(\cos(2t) + \sin(2t)))[/latex] over [latex][-\pi, 3\pi][/latex]
Answer to Exercise 22 - [latex]f(t)=e^{-0.1t}(\cos(2t) + 2\sin(t)))[/latex] over [latex][-\pi, 3\pi][/latex]
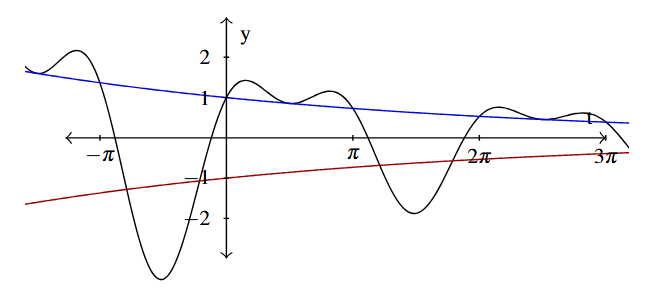
Answer to Exercise 23 - Answers May Vary
- [latex]S(t) = \sin\left(880\pi t\right)[/latex]
- [latex]V(t) = 220 \sqrt{2} \sin\left(120\pi t\right)[/latex]
- [latex]h(t) = 67.5 \sin\left(\frac{\pi}{15} t - \frac{\pi}{2} \right) + 67.5[/latex]
- [latex]x(t) = 67.5 \cos\left(\frac{\pi}{15} t - \frac{\pi}{2} \right) = 67.5 \sin\left(\frac{\pi}{15} t \right)[/latex]
- [latex]h(t) = 28\sin\left(\frac{2\pi}{3} t - \frac{\pi}{2}\right) + 30[/latex]
- .
- [latex]\theta(t) = \theta_{0} \sin\left(\sqrt{\frac{g}{l}}\, t + \frac{\pi}{2}\right)[/latex]
- [latex]\theta(t) = \frac{\pi}{12} \sin\left(4\pi t + \frac{\pi}{2}\right)[/latex]
Section 7.4 Answers
- [latex]\sin(\theta) = \frac{3}{5}, \cos(\theta) = \frac{4}{5}, \tan(\theta) = \frac{3}{4}, \csc(\theta) = \frac{5}{3}, \sec(\theta) = \frac{5}{4}, \cot(\theta) = \frac{4}{3}[/latex]
- [latex]\sin(\theta) = \frac{12}{13}, \cos(\theta) = \frac{5}{13}, \tan(\theta) = \frac{12}{5}, \csc(\theta) = \frac{13}{12}, \sec(\theta) = \frac{13}{5}, \cot(\theta) = \frac{5}{12}[/latex]
- [latex]\sin(\theta) = \frac{24}{25}, \cos(\theta) = \frac{7}{25}, \tan(\theta) = \frac{24}{7}, \csc(\theta) = \frac{25}{24}, \sec(\theta) = \frac{25}{7}, \cot(\theta) = \frac{7}{24}[/latex]
- [latex]\sin(\theta) = \frac{4\sqrt{3}}{7}, \cos(\theta) = \frac{1}{7}, \tan(\theta) = 4\sqrt{3}, \csc(\theta) = \frac{7\sqrt{3}}{12}, \sec(\theta) = 7, \cot(\theta) = \frac{\sqrt{3}}{12}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{91}}{10}, \cos(\theta) = \frac{3}{10}, \tan(\theta) = \frac{\sqrt{91}}{3}, \csc(\theta) = \frac{10\sqrt{91}}{91}, \sec(\theta) = \frac{10}{3}, \cot(\theta) = \frac{3\sqrt{91}}{91}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{530}}{530}, \cos(\theta) = \frac{23\sqrt{530}}{530}, \tan(\theta) = \frac{1}{23}, \csc(\theta) = \sqrt{530}, \sec(\theta) = \frac{\sqrt{530}}{23}, \cot(\theta) = 23[/latex]
- [latex]\sin(\theta) = \frac{2\sqrt{5}}{5}, \cos(\theta) = \frac{\sqrt{5}}{5}, \tan(\theta) = 2, \csc(\theta) = \frac{\sqrt{5}}{2}, \sec(\theta) = \sqrt{5}, \cot(\theta) = \frac{1}{2}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{15}}{4}, \cos(\theta) = \frac{1}{4}, \tan(\theta) = \sqrt{15}, \csc(\theta) = \frac{4\sqrt{15}}{15}, \sec(\theta) = 4, \cot(\theta) = \frac{\sqrt{15}}{15}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{6}}{6}, \cos(\theta) = \frac{\sqrt{30}}{6}, \tan(\theta) = \frac{\sqrt{5}}{5}, \csc(\theta) = \sqrt{6}, \sec(\theta) = \frac{\sqrt{30}}{5}, \cot(\theta) = \sqrt{5}[/latex]
- [latex]\sin(\theta) = \frac{2\sqrt{2}}{3}, \cos(\theta) = \frac{1}{3}, \tan(\theta) = 2\sqrt{2}, \csc(\theta) = \frac{3\sqrt{2}}{4}, \sec(\theta) = 3, \cot(\theta) = \frac{\sqrt{2}}{4}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{5}}{5}, \cos(\theta) = \frac{2\sqrt{5}}{5}, \tan(\theta) = \frac{1}{2}, \csc(\theta) = \sqrt{5}, \sec(\theta) = \frac{\sqrt{5}}{2}, \cot(\theta) = 2[/latex]
- [latex]\sin(\theta) = \frac{1}{5}, \cos(\theta) = \frac{2\sqrt{6}}{5}, \tan(\theta) = \frac{\sqrt{6}}{12}, \csc(\theta) = 5, \sec(\theta) = \frac{5\sqrt{6}}{12}, \cot(\theta) = 2\sqrt{6}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{110}}{11}, \cos(\theta) = \frac{\sqrt{11}}{11}, \tan(\theta) = \sqrt{10}, \csc(\theta) = \frac{\sqrt{110}}{10}, \sec(\theta) = \sqrt{11}, \cot(\theta) = \frac{\sqrt{10}}{10}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{95}}{10}, \cos(\theta) = \frac{\sqrt{5}}{10}, \tan(\theta) = \sqrt{19}, \csc(\theta) = \frac{2\sqrt{95}}{19}, \sec(\theta) = 2\sqrt{5}, \cot(\theta) = \frac{\sqrt{19}}{19}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{21}}{5}, \cos(\theta) = \frac{2}{5}, \tan(\theta) = \frac{\sqrt{21}}{2}, \csc(\theta) = \frac{5\sqrt{21}}{21}, \sec(\theta) = \frac{5}{2}, \cot(\theta) = \frac{2\sqrt{21}}{21}[/latex]
- The tree is about 47 feet tall.
- The lights are about 75 feet apart.
- .
- Answer May Vary
- The fire is about 4581 feet from the base of the tower.
- The Sasquatch ran [latex]200\cot(6^{\circ}) - 200\cot(6.5^{\circ}) \approx 147[/latex] feet in those 10 seconds. This translates to [latex]\approx 10[/latex] miles per hour. At the scene of the second sighting, the Sasquatch was [latex]\approx 1755[/latex] feet from the tower, which means, if it keeps up this pace, it will reach the tower in about 2 minutes.
- The tree is about 41 feet tall.
- The boat has traveled about 244 feet.
- The tower is about 682 feet tall. The guy wire hits the ground about 731 feet away from the base of the tower.
- [latex]\tan \left( \dfrac{\pi}{4} \right) = 1[/latex]
- [latex]\sec \left( \dfrac{\pi}{6} \right) = \dfrac{2\sqrt{3}}{3}[/latex]
- [latex]\csc \left( \dfrac{5\pi}{6} \right) = 2[/latex]
- [latex]\cot \left( \dfrac{4\pi}{3} \right) = \dfrac{\sqrt{3}}{3}[/latex]
- [latex]\tan \left( -\dfrac{11\pi}{6} \right) = \dfrac{\sqrt{3}}{3}[/latex]
- [latex]\sec \left( -\dfrac{3\pi}{2} \right)[/latex] is undefined
- [latex]\csc \left( -\dfrac{\pi}{3} \right) = -\dfrac{2\sqrt{3}}{3}[/latex]
- [latex]\cot \left( \dfrac{13\pi}{2} \right) = 0[/latex]
- [latex]\tan \left( 117\pi \right) = 0[/latex]
- [latex]\sec \left( -\dfrac{5\pi}{3} \right) = 2[/latex]
- [latex]\csc \left( 3\pi \right)[/latex] is undefined
- [latex]\cot \left( -5\pi \right)[/latex] is undefined
- [latex]\tan \left( \dfrac{31\pi}{2} \right)[/latex] is undefined
- [latex]\sec \left( \dfrac{\pi}{4} \right) = \sqrt{2}[/latex]
- [latex]\csc \left( -\dfrac{7\pi}{4} \right) = \sqrt{2}[/latex]
- [latex]\cot \left( \dfrac{7\pi}{6} \right) = \sqrt{3}[/latex]
- [latex]\tan \left( \dfrac{2\pi}{3} \right) = -\sqrt{3}[/latex]
- [latex]\sec \left( -7\pi \right) = -1[/latex]
- [latex]\csc \left( \dfrac{\pi}{2} \right) = 1[/latex]
- [latex]\cot \left( \dfrac{3\pi}{4} \right) = -1[/latex]
- Quadrant II.
- Quadrant III.
- Quadrant I.
- Quadrant IV.
- [latex]\sin(\theta) = \frac{3}{5}, \cos(\theta) = -\frac{4}{5}, \tan(\theta) = -\frac{3}{4}, \csc(\theta) = \frac{5}{3}, \sec(\theta) = -\frac{5}{4}, \cot(\theta) = -\frac{4}{3}[/latex]
- [latex]\sin(\theta) = -\frac{12}{13}, \cos(\theta) = -\frac{5}{13}, \tan(\theta) = \frac{12}{5}, \csc(\theta) = -\frac{13}{12}, \sec(\theta) = -\frac{13}{5}, \cot(\theta) = \frac{5}{12}[/latex]
- [latex]\sin(\theta) = \frac{24}{25}, \cos(\theta) = \frac{7}{25}, \tan(\theta) = \frac{24}{7}, \csc(\theta) = \frac{25}{24}, \sec(\theta) = \frac{25}{7}, \cot(\theta) = \frac{7}{24}[/latex]
- [latex]\sin(\theta) = \frac{-4\sqrt{3}}{7}, \cos(\theta) = \frac{1}{7}, \tan(\theta) = -4\sqrt{3}, \csc(\theta) = -\frac{7\sqrt{3}}{12}, \sec(\theta) = 7, \cot(\theta) = -\frac{\sqrt{3}}{12}[/latex]
- [latex]\sin(\theta) = -\frac{\sqrt{91}}{10}, \cos(\theta) = -\frac{3}{10}, \tan(\theta) = \frac{\sqrt{91}}{3}, \csc(\theta) = -\frac{10\sqrt{91}}{91}, \sec(\theta) = -\frac{10}{3}, \cot(\theta) = \frac{3\sqrt{91}}{91}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{530}}{530}, \cos(\theta) = -\frac{23\sqrt{530}}{530}, \tan(\theta) = -\frac{1}{23}, \csc(\theta) = \sqrt{530}, \sec(\theta) = -\frac{\sqrt{530}}{23}, \cot(\theta) = -23[/latex]
- [latex]\sin(\theta) = -\frac{2\sqrt{5}}{5}, \cos(\theta) = \frac{\sqrt{5}}{5}, \tan(\theta) = -2, \csc(\theta) = -\frac{\sqrt{5}}{2}, \sec(\theta) = \sqrt{5}, \cot(\theta) = -\frac{1}{2}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{15}}{4}, \cos(\theta) = -\frac{1}{4}, \tan(\theta) = -\sqrt{15}, \csc(\theta) = \frac{4\sqrt{15}}{15}, \sec(\theta) = -4, \cot(\theta) = -\frac{\sqrt{15}}{15}[/latex]
- [latex]\sin(\theta) = -\frac{\sqrt{6}}{6}, \cos(\theta) = -\frac{\sqrt{30}}{6}, \tan(\theta) = \frac{\sqrt{5}}{5}, \csc(\theta) = -\sqrt{6}, \sec(\theta) = -\frac{\sqrt{30}}{5}, \cot(\theta) = \sqrt{5}[/latex]
- [latex]\sin(\theta) = \frac{2\sqrt{2}}{3}, \cos(\theta) = \frac{1}{3}, \tan(\theta) = 2\sqrt{2}, \csc(\theta) = \frac{3\sqrt{2}}{4}, \sec(\theta) = 3, \cot(\theta) = \frac{\sqrt{2}}{4}[/latex]
- [latex]\sin(\theta) = \frac{\sqrt{5}}{5}, \cos(\theta) = \frac{2\sqrt{5}}{5}, \tan(\theta) = \frac{1}{2}, \csc(\theta) = \sqrt{5}, \sec(\theta) = \frac{\sqrt{5}}{2}, \cot(\theta) = 2[/latex]
- [latex]\sin(\theta) = \frac{1}{5}, \cos(\theta) = -\frac{2\sqrt{6}}{5}, \tan(\theta) = -\frac{\sqrt{6}}{12}, \csc(\theta) = 5, \sec(\theta) = -\frac{5\sqrt{6}}{12}, \cot(\theta) = -2\sqrt{6}[/latex]
- [latex]\sin(\theta) = -\frac{\sqrt{110}}{11}, \cos(\theta) = -\frac{\sqrt{11}}{11}, \tan(\theta) = \sqrt{10}, \csc(\theta) = -\frac{\sqrt{110}}{10}, \sec(\theta) = -\sqrt{11}, \cot(\theta) = \frac{\sqrt{10}}{10}[/latex]
- [latex]\sin(\theta) = -\frac{\sqrt{95}}{10}, \cos(\theta) = \frac{\sqrt{5}}{10}, \tan(\theta) = -\sqrt{19}, \csc(\theta) = -\frac{2\sqrt{95}}{19}, \sec(\theta) = 2\sqrt{5}, \cot(\theta) = -\frac{\sqrt{19}}{19}[/latex]
- [latex]\csc(78.95^{\circ}) \approx 1.019[/latex]
- [latex]\tan(-2.01) \approx 2.129[/latex]
- [latex]\cot(392.994) \approx 3.292[/latex]
- [latex]\sec(207^{\circ}) \approx -1.122[/latex]
- [latex]\csc(5.902) \approx -2.688[/latex]
- [latex]\tan(39.672^{\circ}) \approx 0.829[/latex]
- [latex]\cot(3^{\circ}) \approx 19.081[/latex]
- [latex]\sec(0.45) \approx 1.111[/latex]
- [latex]\tan(\theta) = \sqrt{3}[/latex] when [latex]\theta = \dfrac{\pi}{3} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\sec(\theta) = 2[/latex] when [latex]\theta = \dfrac{\pi}{3} + 2\pi k[/latex] or [latex]\theta = \dfrac{5\pi}{3} + 2\pi k[/latex] for any integer [latex]k[/latex]
- [latex]\csc(\theta) = -1[/latex] when [latex]\theta = \dfrac{3\pi}{2} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cot(\theta) = \dfrac{\sqrt{3}}{3}[/latex] when [latex]\theta = \dfrac{\pi}{3} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\tan(\theta) = 0[/latex] when [latex]\theta = \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\sec(\theta) = 1[/latex] when [latex]\theta = 2\pi k[/latex] for any integer [latex]k[/latex]
- [latex]\csc(\theta) = 2[/latex] when [latex]\theta = \dfrac{\pi}{6} + 2\pi k[/latex] or [latex]\theta = \dfrac{5\pi}{6} + 2\pi k[/latex] for any integer [latex]k[/latex].
- [latex]\cot(\theta) = 0[/latex] when [latex]\theta = \dfrac{\pi}{2} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\tan(\theta) = -1[/latex] when [latex]\theta = \dfrac{3\pi}{4} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\sec(\theta) = 0[/latex] never happens
- [latex]\csc(\theta) = -\dfrac{1}{2}[/latex] never happens
- [latex]\sec(\theta) = -1[/latex] when [latex]\theta = \pi + 2\pi k = (2k+1)\pi[/latex] for any integer [latex]k[/latex]
- [latex]\tan(\theta) = -\sqrt{3}[/latex] when [latex]\theta = \dfrac{2\pi}{3} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\csc(\theta) = -2[/latex] when [latex]\theta = \dfrac{7\pi}{6} + 2\pi k[/latex] or [latex]\theta = \dfrac{11\pi}{6} + 2\pi k[/latex] for any integer [latex]k[/latex]
- [latex]\cot(\theta) = -1[/latex] when [latex]\theta = \dfrac{3\pi}{4} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\cot(t) = 1[/latex] when [latex]t = \dfrac{\pi}{4} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\tan(t) = \dfrac{\sqrt{3}}{3}[/latex] when [latex]t = \dfrac{\pi}{6} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\sec(t) = -\dfrac{2\sqrt{3}}{3}[/latex] when [latex]t = \dfrac{5\pi}{6} + 2\pi k[/latex] or [latex]t = \dfrac{7\pi}{6} + 2\pi k[/latex] for any integer [latex]k[/latex]
- [latex]\csc(t) = 0[/latex] never happens
- [latex]\cot(t) = -\sqrt{3}[/latex] when [latex]t = \dfrac{5\pi}{6} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\tan(t) = -\dfrac{\sqrt{3}}{3}[/latex] when [latex]t = \dfrac{5\pi}{6} + \pi k[/latex] for any integer [latex]k[/latex]
- [latex]\sec(t) = \dfrac{2\sqrt{3}}{3}[/latex] when [latex]t = \dfrac{\pi}{6} + 2\pi k[/latex] or [latex]t = \dfrac{11\pi}{6} + 2\pi k[/latex] for any integer [latex]k[/latex]
- [latex]\csc(t) = \dfrac{2\sqrt{3}}{3}[/latex] when [latex]t = \dfrac{\pi}{3} + 2\pi k[/latex] or [latex]t = \dfrac{2\pi}{3} + 2\pi k[/latex] for any integer [latex]k[/latex]
- One solution is [latex]g(t) = 3t^2[/latex] and [latex]h(t) = 2\tan(3t)[/latex].
- One solution is [latex]g(\theta) = \sec(\theta)[/latex] and [latex]h(\theta) = \tan(\theta)[/latex].
- One solution is [latex]g(t) = -\csc(t)[/latex] and [latex]h(t) = \cot(t)[/latex].
- One solution is [latex]f(t) = \tan(3t)[/latex] and [latex]g(t) = t[/latex].
- One solution is [latex]f(\theta) = 4 \theta[/latex] and [latex]g(\theta) = \tan(\theta)[/latex].
- As [latex]\sec^{2}(\theta) = (\sec(\theta))^2[/latex], one solution is [latex]f(\theta) = \sec(\theta)[/latex] and [latex]g(\theta) = \theta^2[/latex].
- One solution is [latex]f(x) = \sin(x)[/latex] and [latex]g(x) = \ln(x)[/latex].
- One solution is [latex]f(\theta) = \sec(\theta)[/latex], [latex]g(\theta) = \tan(\theta)[/latex], and [latex]h(\theta) = \ln| \theta|[/latex].
- Answer May Vary
- As we zoom in towards 0, the average rate of change of [latex]\tan(k t)[/latex] approaches [latex]k[/latex]. This is the same trend we observed for [latex]\sin(k t)[/latex] in Section 7.2 number 65.
![A table with five rows and 4 columns. The first row is the header row with T(t), [-0.1, 0.1], [-0.01, 0.01], and [-0.001, 0.001]. The first column has the functions tangent of t, tangent of 2t, tangent of 3t, and tangent of 4t. The remaining entries are the values of the functions over the intervals.](https://odp.library.tamu.edu/app/uploads/sites/96/2025/06/Answer_7_4_100.png)
Section 7.5 Answers
- [latex]y = \tan \left(t - \dfrac{\pi}{3} \right)[/latex]
Period: [latex]\pi[/latex]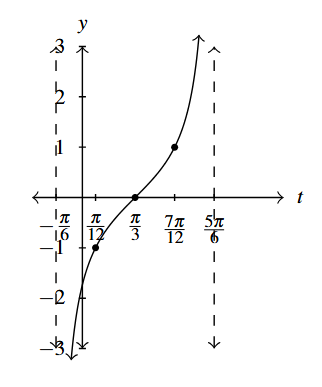
Answer to Exercise 1 - [latex]y = 2\tan \left( \dfrac{1}{4}t \right) - 3[/latex]
Period: [latex]4\pi[/latex]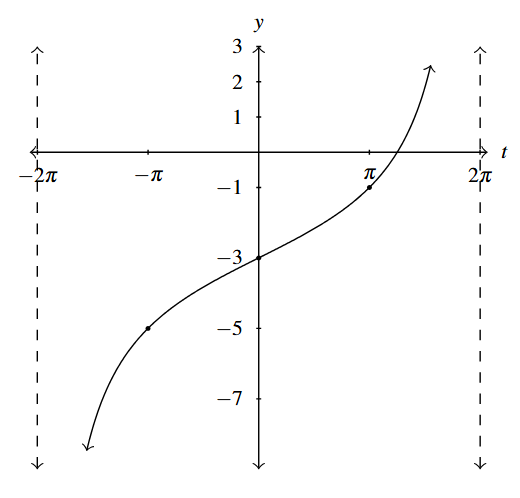
Answer to Exercise 2 - [latex]y = \dfrac{1}{3}\tan(-2t - \pi) + 1[/latex] is equivalent to [latex]y = -\dfrac{1}{3}\tan(2t + \pi) + 1[/latex] via the Even / Odd identity for tangent.
Period: [latex]\dfrac{\pi}{2}[/latex]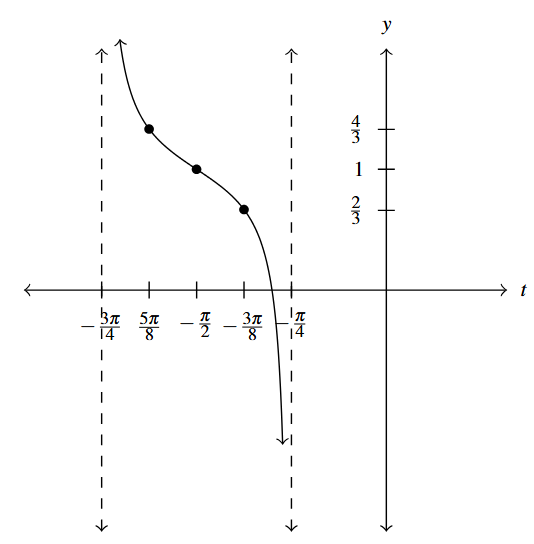
Answer to Exercise 3 - [latex]y = \sec \left( t - \frac{\pi}{2} \right)[/latex]
Start with [latex]y = \cos \left( t - \frac{\pi}{2} \right)[/latex]
Period: [latex]2\pi[/latex]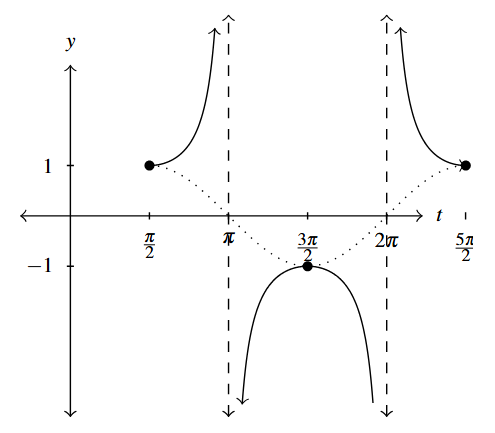
Answer to Exercise 4 - [latex]y = -\csc \left( t + \dfrac{\pi}{3} \right)[/latex]
Start with [latex]y = -\sin \left( t + \dfrac{\pi}{3} \right)[/latex]
Period: [latex]2\pi[/latex]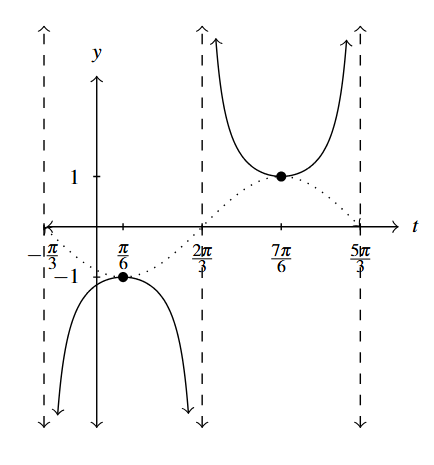
Answer to Exercise 5 - [latex]y = -\dfrac{1}{3} \sec \left( \dfrac{1}{2}t + \dfrac{\pi}{3} \right)[/latex]
Start with [latex]y = -\dfrac{1}{3}\cos \left( \dfrac{1}{2}t + \dfrac{\pi}{3} \right)[/latex]
Period: [latex]4\pi[/latex]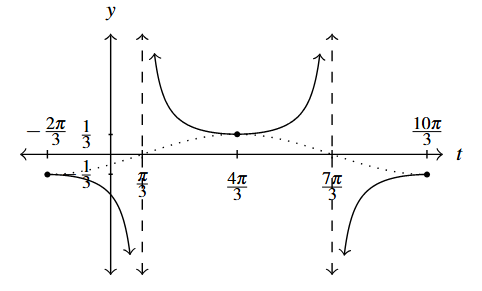
Answer to Exercise 6 - [latex]y = \csc (2t - \pi)[/latex]
Start with [latex]y = \sin(2t - \pi)[/latex]
Period: [latex]\pi[/latex]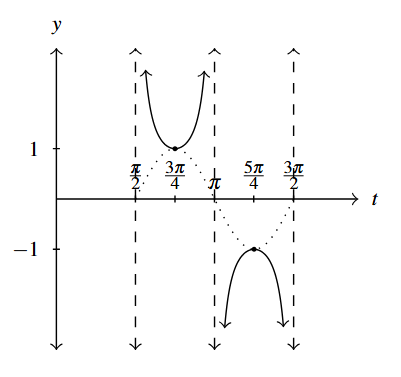
Answer to Exercise 7 - [latex]y = \sec(3t - 2\pi) + 4[/latex]
Start with [latex]y = \cos (3t - 2\pi) + 4[/latex]
Period: [latex]\dfrac{2\pi}{3}[/latex]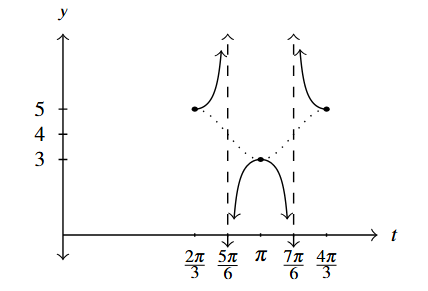
Answer to Exercise 8 - [latex]y = \csc \left( -t - \dfrac{\pi}{4} \right) - 2[/latex]
Start with [latex]y = \sin \left( -t - \dfrac{\pi}{4} \right) - 2[/latex]
Period: [latex]2\pi[/latex]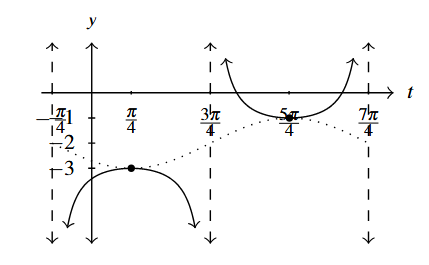
Answer to Exercise 9 - [latex]y = \cot \left( t + \dfrac{\pi}{6} \right)[/latex]
Period: [latex]\pi[/latex]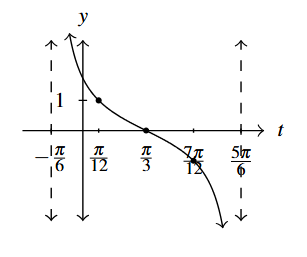
Answer to Exercise 10 - [latex]y = -11\cot \left( \dfrac{1}{5} t \right)[/latex]
Period: [latex]5\pi[/latex]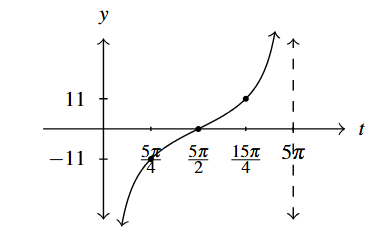
Answer to Exercise 11 - [latex]y = \dfrac{1}{3} \cot \left( 2t + \dfrac{3\pi}{2} \right) + 1[/latex]
Period: [latex]\dfrac{\pi}{2}[/latex]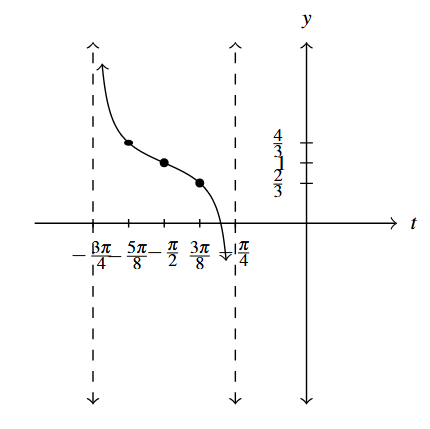
Answer to Exercise 12 - [latex]F(t) = 2 \sec(t-\pi)[/latex], [latex]G(t) = 2 \csc \left(t - \frac{\pi}{2} \right)[/latex]
- [latex]F(t) = \sec\left( \frac{\pi}{2} t \right) + 1[/latex], [latex]G(t) = \csc\left( \frac{\pi}{2} t + \frac{\pi}{2} \right) + 1[/latex]
- [latex]J(t) = -\tan\left(t+ \frac{\pi}{4} \right)[/latex], [latex]K(t) = \cot \left(t - \frac{\pi}{4} \right)[/latex]
- [latex]J(t) = \tan\left( \frac{\pi}{4} t \right) + 1[/latex], [latex]K(t) = -\cot\left( \frac{\pi}{4} t + \frac{\pi}{2} \right) + 1[/latex]
- .
- [latex]\csc\left(t + \frac{\pi}{2} \right) = \sec(t)[/latex] and [latex]\sec\left(t - \frac{\pi}{2} \right) = \csc(t)[/latex].
- [latex]f(t) = \sec\left( 2 t - \frac{7\pi}{6} \right) -1 = \csc\left( \left[2 t - \frac{7\pi}{6}\right] + \frac{\pi}{2} \right) -1 = \csc\left( 2 t - \frac{2\pi}{3} \right) -1[/latex], in terms of cosecants.
- [latex]f(t) = - \sec\left(2t - \frac{\pi}{6} \right)-1[/latex] and [latex]f(t) = -\csc\left(2t + \frac{\pi}{3} \right) -1[/latex] are two answers
Section 7.6 Answers
- [latex]\arcsin \left( -1 \right) = -\dfrac{\pi}{2}[/latex]
- [latex]\arcsin \left( -\dfrac{\sqrt{3}}{2} \right) = -\dfrac{\pi}{3}[/latex]
- [latex]\arcsin \left( -\dfrac{\sqrt{2}}{2} \right) = -\dfrac{\pi}{4}[/latex]
- [latex]\arcsin \left( -\dfrac{1}{2} \right) = -\dfrac{\pi}{6}[/latex]
- [latex]\arcsin \left( 0 \right) = 0[/latex]
- [latex]\arcsin \left( \dfrac{1}{2} \right) = \dfrac{\pi}{6}[/latex]
- [latex]\arcsin \left( \dfrac{\sqrt{2}}{2} \right) = \dfrac{\pi}{4}[/latex]
- [latex]\arcsin \left( \dfrac{\sqrt{3}}{2} \right) = \dfrac{\pi}{3}[/latex]
- [latex]\arcsin \left( 1 \right) = \dfrac{\pi}{2}[/latex]
- [latex]\arccos \left( -1 \right) = \pi[/latex]
- [latex]\arccos \left( -\dfrac{\sqrt{3}}{2} \right) = \dfrac{5\pi}{6}[/latex]
- [latex]\arccos \left( -\dfrac{\sqrt{2}}{2} \right) = \dfrac{3\pi}{4}[/latex]
- [latex]\arccos \left( -\dfrac{1}{2} \right) = \dfrac{2\pi}{3}[/latex]
- [latex]\arccos \left( 0 \right) = \dfrac{\pi}{2}[/latex]
- [latex]\arccos \left( \dfrac{1}{2} \right) = \dfrac{\pi}{3}[/latex]
- [latex]\arccos \left( \dfrac{\sqrt{2}}{2} \right) = \dfrac{\pi}{4}[/latex]
- [latex]\arccos \left( \dfrac{\sqrt{3}}{2} \right) = \dfrac{\pi}{6}[/latex]
- [latex]\arccos \left( 1 \right) = 0[/latex]
- [latex]\arctan \left( -\sqrt{3} \right) = -\dfrac{\pi}{3}[/latex]
- [latex]\arctan \left( -1 \right) = -\dfrac{\pi}{4}[/latex]
- [latex]\arctan \left( -\dfrac{\sqrt{3}}{3} \right) = -\dfrac{\pi}{6}[/latex]
- [latex]\arctan \left( 0 \right) = 0[/latex]
- [latex]\arctan \left( \dfrac{\sqrt{3}}{3} \right) = \dfrac{\pi}{6}[/latex]
- [latex]\arctan \left( 1 \right) = \dfrac{\pi}{4}[/latex]
- [latex]\arctan \left( \sqrt{3} \right) = \dfrac{\pi}{3}[/latex]
- [latex]\text{arccot} \left( -\sqrt{3} \right) = \dfrac{5\pi}{6}[/latex]
- [latex]\text{arccot} \left( -1 \right) = \dfrac{3\pi}{4}[/latex]
- [latex]\text{arccot} \left( -\dfrac{\sqrt{3}}{3} \right) = \dfrac{2\pi}{3}[/latex]
- [latex]\text{arccot} \left( 0 \right) = \dfrac{\pi}{2}[/latex]
- [latex]\text{arccot} \left( \dfrac{\sqrt{3}}{3} \right) = \dfrac{\pi}{3}[/latex]
- [latex]\text{arccot} \left( 1 \right) = \dfrac{\pi}{4}[/latex]
- [latex]\text{arccot} \left( \sqrt{3} \right) = \dfrac{\pi}{6}[/latex]
- [latex]\text{arcsec} \left( 2 \right) = \dfrac{\pi}{3}[/latex]
- [latex]\text{arccsc} \left( 2 \right) = \dfrac{\pi}{6}[/latex]
- [latex]\text{arcsec} \left( \sqrt{2} \right) = \dfrac{\pi}{4}[/latex]
- [latex]\text{arccsc} \left( \sqrt{2} \right) = \dfrac{\pi}{4}[/latex]
- [latex]\text{arcsec} \left( \dfrac{2\sqrt{3}}{3} \right) = \dfrac{\pi}{6}[/latex]
- [latex]\text{arccsc} \left( \dfrac{2\sqrt{3}}{3} \right) = \dfrac{\pi}{3}[/latex]
- [latex]\text{arcsec} \left( 1 \right) = 0[/latex]
- [latex]\text{arccsc} \left( 1 \right) = \dfrac{\pi}{2}[/latex]
- [latex]\text{arcsec} \left( -2 \right) = \dfrac{2\pi}{3}[/latex]
- [latex]\text{arcsec} \left( -\sqrt{2} \right) = \dfrac{3\pi}{4}[/latex]
- [latex]\text{arcsec} \left( -\dfrac{2\sqrt{3}}{3} \right) = \dfrac{5\pi}{6}[/latex]
- [latex]\text{arcsec} \left( -1 \right) = \pi[/latex]
- [latex]\text{arccsc} \left( -2 \right) = -\dfrac{\pi}{6}[/latex]
- [latex]\text{arccsc} \left( -\sqrt{2} \right) = -\dfrac{\pi}{4}[/latex]
- [latex]\text{arccsc} \left( -\dfrac{2\sqrt{3}}{3} \right) = -\dfrac{\pi}{3}[/latex]
- [latex]\text{arccsc} \left( -1 \right) = -\dfrac{\pi}{2}[/latex]
- [latex]\text{arcsec} \left( -2 \right) = \dfrac{4\pi}{3}[/latex]
- [latex]\text{arcsec} \left( -\sqrt{2} \right) = \dfrac{5\pi}{4}[/latex]
- [latex]\text{arcsec} \left( -\dfrac{2\sqrt{3}}{3} \right) = \dfrac{7\pi}{6}[/latex]
- [latex]\text{arcsec} \left( -1 \right) = \pi[/latex]
- [latex]\text{arccsc} \left( -2 \right) = \dfrac{7\pi}{6}[/latex]
- [latex]\text{arccsc} \left( -\sqrt{2} \right) = \dfrac{5\pi}{4}[/latex]
- [latex]\text{arccsc} \left( -\dfrac{2\sqrt{3}}{3} \right) = \dfrac{4\pi}{3}[/latex]
- [latex]\text{arccsc} \left( -1 \right) = \dfrac{3\pi}{2}[/latex]
- [latex]\sin\left(\arcsin\left(\dfrac{1}{2}\right)\right) = \dfrac{1}{2}[/latex]
- [latex]\sin\left(\arcsin\left(-\dfrac{\sqrt{2}}{2}\right)\right) = -\dfrac{\sqrt{2}}{2}[/latex]
- [latex]\sin\left(\arcsin\left(\dfrac{3}{5}\right)\right) = \dfrac{3}{5}[/latex]
- [latex]\sin\left(\arcsin\left(-0.42\right)\right) = -0.42[/latex]
- [latex]\sin\left(\arcsin\left(\dfrac{5}{4}\right)\right)[/latex] is undefined.
- [latex]\cos\left(\arccos\left(\dfrac{\sqrt{2}}{2}\right)\right) = \dfrac{\sqrt{2}}{2}[/latex]
- [latex]\cos\left(\arccos\left(-\dfrac{1}{2}\right)\right) = -\dfrac{1}{2}[/latex]
- [latex]\cos\left(\arccos\left(\dfrac{5}{13}\right)\right) = \dfrac{5}{13}[/latex]
- [latex]\cos\left(\arccos\left(-0.998\right)\right) = -0.998[/latex]
- [latex]\cos\left(\arccos\left(\pi \right)\right)[/latex] is undefined.
- [latex]\tan\left(\arctan\left(-1\right)\right) = -1[/latex]
- [latex]\tan\left(\arctan\left(\sqrt{3}\right)\right) = \sqrt{3}[/latex]
- [latex]\tan\left(\arctan\left(\dfrac{5}{12}\right)\right) = \dfrac{5}{12}[/latex]
- [latex]\tan\left(\arctan\left(0.965\right)\right) = 0.965[/latex]
- [latex]\tan\left(\arctan\left( 3\pi \right)\right) = 3\pi[/latex]
- [latex]\cot\left(\text{arccot}\left(1\right)\right) = 1[/latex]
- [latex]\cot\left(\text{arccot}\left(-\sqrt{3}\right)\right) = -\sqrt{3}[/latex]
- [latex]\cot\left(\text{arccot}\left(-\dfrac{7}{24}\right)\right) = -\dfrac{7}{24}[/latex]
- [latex]\cot\left(\text{arccot}\left(-0.001\right)\right) = -0.001[/latex]
- [latex]\cot\left(\text{arccot}\left( \dfrac{17\pi}{4} \right)\right) = \dfrac{17\pi}{4}[/latex]
- [latex]\sec\left(\text{arcsec}\left(2\right)\right) = 2[/latex]
- [latex]\sec\left(\text{arcsec}\left(-1\right)\right) = -1[/latex]
- [latex]\sec\left(\text{arcsec}\left(\dfrac{1}{2}\right)\right)[/latex] is undefined.
- [latex]\sec\left(\text{arcsec}\left(0.75\right)\right)[/latex] is undefined.
- [latex]\sec\left(\text{arcsec}\left( 117\pi \right)\right)= 117\pi[/latex]
- [latex]\csc\left(\text{arccsc}\left(\sqrt{2}\right)\right) = \sqrt{2}[/latex]
- [latex]\csc\left(\text{arccsc}\left(-\dfrac{2\sqrt{3}}{3}\right)\right) = -\dfrac{2\sqrt{3}}{3}[/latex]
- [latex]\csc\left(\text{arccsc}\left(\dfrac{\sqrt{2}}{2}\right)\right)[/latex] is undefined.
- [latex]\csc\left(\text{arccsc}\left(1.0001\right)\right) = 1.0001[/latex]
- [latex]\csc\left(\text{arccsc}\left( \dfrac{\pi}{4} \right)\right)[/latex] is undefined.
- [latex]\arcsin\left(\sin\left(\dfrac{\pi}{6}\right) \right) = \dfrac{\pi}{6}[/latex]
- [latex]\arcsin\left(\sin\left(-\dfrac{\pi}{3}\right) \right) = -\dfrac{\pi}{3}[/latex]
- [latex]\arcsin\left(\sin\left(\dfrac{3\pi}{4}\right) \right) = \dfrac{\pi}{4}[/latex]
- [latex]\arcsin\left(\sin\left(\dfrac{11\pi}{6}\right) \right) = -\dfrac{\pi}{6}[/latex]
- [latex]\arcsin\left(\sin\left(\dfrac{4\pi}{3}\right) \right) = -\dfrac{\pi}{3}[/latex]
- [latex]\arccos\left(\cos\left(\dfrac{\pi}{4}\right) \right) = \dfrac{\pi}{4}[/latex]
- [latex]\arccos\left(\cos\left(\dfrac{2\pi}{3}\right) \right) = \dfrac{2\pi}{3}[/latex]
- [latex]\arccos\left(\cos\left(\dfrac{3\pi}{2}\right) \right) = \dfrac{\pi}{2}[/latex]
- [latex]\arccos\left(\cos\left(-\dfrac{\pi}{6}\right) \right) = \dfrac{\pi}{6}[/latex]
- [latex]\arccos\left(\cos\left(\dfrac{5\pi}{4}\right) \right) = \dfrac{3\pi}{4}[/latex]
- [latex]\arctan\left(\tan\left(\dfrac{\pi}{3}\right) \right) = \dfrac{\pi}{3}[/latex]
- [latex]\arctan\left(\tan\left(-\dfrac{\pi}{4}\right) \right) = -\dfrac{\pi}{4}[/latex]
- [latex]\arctan\left(\tan\left(\pi\right) \right) = 0[/latex]
- [latex]\arctan\left(\tan\left(\dfrac{\pi}{2}\right) \right)[/latex] is undefined
- [latex]\arctan\left(\tan\left(\dfrac{2\pi}{3}\right) \right) = -\dfrac{\pi}{3}[/latex]
- [latex]\text{arccot}\left(\cot\left(\dfrac{\pi}{3}\right) \right) = \dfrac{\pi}{3}[/latex]
- [latex]\text{arccot}\left(\cot\left(-\dfrac{\pi}{4}\right) \right) = \dfrac{3\pi}{4}[/latex]
- [latex]\text{arccot}\left(\cot\left(\pi\right) \right)[/latex] is undefined
- [latex]\text{arccot}\left(\cot\left(\dfrac{3\pi}{2}\right) \right) = \dfrac{\pi}{2}[/latex]
- [latex]\text{arccot}\left(\cot\left(\dfrac{2\pi}{3}\right) \right) = \dfrac{2\pi}{3}[/latex]
- [latex]\text{arcsec}\left(\sec\left(\dfrac{\pi}{4}\right) \right) = \dfrac{\pi}{4}[/latex]
- [latex]\text{arcsec}\left(\sec\left(\dfrac{4\pi}{3}\right) \right) = \dfrac{2\pi}{3}[/latex]
- [latex]\text{arcsec}\left(\sec\left( \dfrac{5\pi}{6} \right) \right) = \dfrac{5\pi}{6}[/latex]
- [latex]\text{arcsec}\left(\sec\left(-\dfrac{\pi}{2} \right) \right)[/latex] is undefined.
- [latex]\text{arcsec}\left(\sec\left(\dfrac{5\pi}{3}\right) \right) = \dfrac{\pi}{3}[/latex]
- [latex]\text{arccsc}\left(\csc\left(\dfrac{\pi}{6}\right) \right) = \dfrac{\pi}{6}[/latex]
- [latex]\text{arccsc}\left(\csc\left(\dfrac{5\pi}{4}\right) \right) = -\dfrac{\pi}{4}[/latex]
- [latex]\text{arccsc}\left(\csc\left( \dfrac{2\pi}{3} \right) \right) = \dfrac{\pi}{3}[/latex]
- [latex]\text{arccsc}\left(\csc\left(-\dfrac{\pi}{2} \right) \right) = -\dfrac{\pi}{2}[/latex]
- [latex]\text{arccsc}\left(\csc\left(\dfrac{11\pi}{6}\right) \right) = -\dfrac{\pi}{6}[/latex]
- [latex]\text{arcsec}\left(\sec\left(\dfrac{11\pi}{12}\right) \right) = \dfrac{11\pi}{12}[/latex]
- [latex]\text{arccsc}\left(\csc\left(\dfrac{9\pi}{8}\right) \right) = -\dfrac{\pi}{8}[/latex]
- [latex]\text{arcsec}\left(\sec\left(\dfrac{\pi}{4}\right) \right) = \dfrac{\pi}{4}[/latex]
- [latex]\text{arcsec}\left(\sec\left(\dfrac{4\pi}{3}\right) \right) = \dfrac{4\pi}{3}[/latex]
- [latex]\text{arcsec}\left(\sec\left( \dfrac{5\pi}{6} \right) \right) = \dfrac{7\pi}{6}[/latex]
- [latex]\text{arcsec}\left(\sec\left(-\dfrac{\pi}{2} \right) \right)[/latex] is undefined.
- [latex]\text{arcsec}\left(\sec\left(\dfrac{5\pi}{3}\right) \right) = \dfrac{\pi}{3}[/latex]
- [latex]\text{arccsc}\left(\csc\left(\dfrac{\pi}{6}\right) \right) = \dfrac{\pi}{6}[/latex]
- [latex]\text{arccsc}\left(\csc\left(\dfrac{5\pi}{4}\right) \right) = \dfrac{5\pi}{4}[/latex]
- [latex]\text{arccsc}\left(\csc\left( \dfrac{2\pi}{3} \right) \right) = \dfrac{\pi}{3}[/latex]
- [latex]\text{arccsc}\left(\csc\left(-\dfrac{\pi}{2} \right) \right) = \dfrac{3\pi}{2}[/latex]
- [latex]\text{arccsc}\left(\csc\left(\dfrac{11\pi}{6}\right) \right) = \dfrac{7\pi}{6}[/latex]
- [latex]\text{arcsec}\left(\sec\left(\dfrac{11\pi}{12}\right) \right) = \dfrac{13\pi}{12}[/latex]
- [latex]\text{arccsc}\left(\csc\left(\dfrac{9\pi}{8}\right) \right) = \dfrac{9\pi}{8}[/latex]
- [latex]\sin\left(\arccos\left(-\dfrac{1}{2}\right)\right) = \dfrac{\sqrt{3}}{2}[/latex]
- [latex]\sin\left(\arccos\left(\dfrac{3}{5}\right)\right) = \dfrac{4}{5}[/latex]
- [latex]\sin\left(\arctan\left(-2\right)\right) = -\dfrac{2\sqrt{5}}{5}[/latex]
- [latex]\sin\left(\text{arccot}\left(\sqrt{5}\right)\right) = \dfrac{\sqrt{6}}{6}[/latex]
- [latex]\sin\left(\text{arccsc}\left(-3\right)\right) = -\dfrac{1}{3}[/latex]
- [latex]\cos\left(\arcsin\left(-\dfrac{5}{13}\right)\right) = \dfrac{12}{13}[/latex]
- [latex]\cos\left(\arctan\left(\sqrt{7} \right)\right) = \dfrac{\sqrt{2}}{4}[/latex]
- [latex]\cos\left(\text{arccot}\left( 3 \right)\right) = \dfrac{3\sqrt{10}}{10}[/latex]
- [latex]\cos\left(\text{arcsec}\left( 5 \right)\right) = \dfrac{1}{5}[/latex]
- [latex]\tan\left(\arcsin\left(-\dfrac{2\sqrt{5}}{5}\right)\right)=-2[/latex]
- [latex]\tan\left(\arccos\left(-\dfrac{1}{2}\right)\right) = -\sqrt{3}[/latex]
- [latex]\tan\left(\text{arcsec}\left(\dfrac{5}{3}\right)\right) = \dfrac{4}{3}[/latex]
- [latex]\tan\left(\text{arccot}\left( 12 \right)\right) = \dfrac{1}{12}[/latex]
- [latex]\cot\left(\arcsin\left(\dfrac{12}{13}\right)\right) = \dfrac{5}{12}[/latex]
- [latex]\cot\left(\arccos\left(\dfrac{\sqrt{3}}{2}\right)\right) = \sqrt{3}[/latex]
- [latex]\cot\left(\text{arccsc}\left(\sqrt{5}\right)\right) = 2[/latex]
- [latex]\cot\left(\arctan \left( 0.25 \right)\right) = 4[/latex]
- [latex]\sec\left(\arccos\left(\dfrac{\sqrt{3}}{2}\right)\right) = \dfrac{2\sqrt{3}}{3}[/latex]
- [latex]\sec\left(\arcsin\left(-\dfrac{12}{13}\right)\right) = \dfrac{13}{5}[/latex]
- [latex]\sec\left(\arctan\left(10\right)\right) = \sqrt{101}[/latex]
- [latex]\sec\left(\text{arccot}\left(-\dfrac{\sqrt{10}}{10}\right)\right) = -\sqrt{11}[/latex]
- [latex]\csc\left(\text{arccot}\left(9 \right)\right) = \sqrt{82}[/latex]
- [latex]\csc\left(\arcsin\left(\dfrac{3}{5}\right)\right) = \dfrac{5}{3}[/latex]
- [latex]\csc\left(\arctan\left(-\dfrac{2}{3}\right)\right) = -\dfrac{\sqrt{13}}{2}[/latex]
- [latex]\sin\left(\arcsin\left( \dfrac{5}{13} \right) + \dfrac{\pi}{4}\right) = \dfrac{17\sqrt{2}}{26}[/latex]
- [latex]\cos\left( \text{arcsec}(3) + \arctan(2) \right) = \dfrac{\sqrt{5} - 4\sqrt{10}}{15}[/latex]
- [latex]\tan\left( \arctan(3) + \arccos\left(-\dfrac{3}{5}\right) \right) = \dfrac{1}{3}[/latex]
- [latex]\sin\left(2\arcsin\left(-\dfrac{4}{5}\right)\right)= -\dfrac{24}{25}[/latex]
- [latex]\sin\left(2\text{arccsc}\left(\dfrac{13}{5}\right)\right) = \dfrac{120}{169}[/latex]
- [latex]\sin\left(2\arctan\left(2\right)\right) = \dfrac{4}{5}[/latex]
- [latex]\cos\left(2 \arcsin\left(\dfrac{3}{5}\right)\right) = \dfrac{7}{25}[/latex]
- [latex]\cos\left(2 \text{arcsec}\left(\dfrac{25}{7}\right)\right) = -\dfrac{527}{625}[/latex]
- [latex]\cos\left(2 \text{arccot}\left(-\sqrt{5}\right)\right) = \dfrac{2}{3}[/latex]
- [latex]\sin\left( \dfrac{\arctan(2)}{2} \right) = \sqrt{\dfrac{5-\sqrt{5}}{10}}[/latex]
- [latex]f(x) = \sin \left( \arccos \left( x \right) \right) = \sqrt{1 - x^{2}}[/latex] for [latex]-1 \leq x \leq 1[/latex]
- [latex]f(x) = \cos \left( \arctan \left( x \right) \right) = \dfrac{1}{\sqrt{1 + x^{2}}}[/latex] for all [latex]x[/latex]
- [latex]f(x) =\tan \left( \arcsin \left( x \right) \right) = \dfrac{x}{\sqrt{1 - x^{2}}}[/latex] for [latex]-1[/latex] < [latex]x[/latex] < 1
- [latex]f(x) =\sec \left( \arctan \left( x \right) \right) = \sqrt{1 + x^{2}}[/latex] for all [latex]x[/latex]
- [latex]f(x) =\csc \left( \arccos \left( x \right) \right) = \dfrac{1}{\sqrt{1 - x^{2}}}[/latex] for [latex]-1[/latex] < [latex]x[/latex] < 1
- [latex]f(x) =\sin \left( 2\arctan \left( x \right) \right) = \dfrac{2x}{x^{2} + 1}[/latex] for all [latex]x[/latex]
- [latex]f(x) =\sin \left( 2\arccos \left( x \right) \right) = 2x\sqrt{1-x^2}[/latex] for [latex]-1 \leq x \leq 1[/latex]
- [latex]f(x) =\cos \left( 2\arctan \left( x \right) \right) = \dfrac{1 - x^{2}}{1 + x^{2}}[/latex] for all [latex]x[/latex]
- [latex]f(x) =\sin(\arccos(2x)) = \sqrt{1-4x^2}[/latex] for [latex]-\frac{1}{2} \leq x \leq \frac{1}{2}[/latex]
- [latex]f(x) =\sin\left(\arccos\left(\dfrac{x}{5}\right)\right) = \dfrac{\sqrt{25-x^2}}{5}[/latex] for [latex]-5 \leq x \leq 5[/latex]
- [latex]f(x) =\cos\left(\arcsin\left(\dfrac{x}{2}\right)\right) = \dfrac{\sqrt{4-x^2}}{2}[/latex] for [latex]-2 \leq x \leq 2[/latex]
- [latex]f(x) =\cos\left(\arctan\left(3x\right)\right) = \dfrac{1}{\sqrt{1+9x^{2}}}[/latex] for all [latex]x[/latex]
- [latex]f(x) =\sin(2\arcsin(7x)) = 14x \sqrt{1-49x^2}[/latex] for [latex]-\dfrac{1}{7} \leq x \leq \dfrac{1}{7}[/latex]
- [latex]f(x) =\sin\left(2 \arcsin\left( \dfrac{x\sqrt{3}}{3} \right) \right) = \dfrac{2x\sqrt{3-x^2}}{3}[/latex] for [latex]-\sqrt{3} \leq x \leq \sqrt{3}[/latex]
- [latex]f(x) =\cos(2 \arcsin(4x)) = 1 - 32x^2[/latex] for [latex]-\dfrac{1}{4} \leq x \leq \dfrac{1}{4}[/latex]
- [latex]f(x) =\sec(\arctan(2x))\tan(\arctan(2x)) = 2x \sqrt{1+4x^2}[/latex] for all [latex]x[/latex]
- [latex]f(x) =\sin \left( \arcsin(x) + \arccos(x) \right) = 1[/latex] for [latex]-1 \leq x \leq 1[/latex]
- [latex]f(x) =\cos \left( \arcsin(x) + \arctan(x) \right) = \dfrac{\sqrt{1 - x^{2}} - x^{2}}{\sqrt{1 + x^{2}}}[/latex] for [latex]-1 \leq x \leq 1[/latex]
- [4] [latex]f(x) =\tan \left( 2\arcsin(x) \right) = \dfrac{2x\sqrt{1 - x^{2}}}{1 - 2x^{2}}[/latex] for [latex]x[/latex] in [latex]\left(-1, -\dfrac{\sqrt{2}}{2}\right) \cup \left(-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2} \right) \cup \left(\dfrac{\sqrt{2}}{2}, 1\right)[/latex]
- [latex]f(x) =\sin \left( \dfrac{1}{2}\arctan(x) \right) = \left\{ \begin{array}{rr} \sqrt{\dfrac{\sqrt{x^{2} + 1} - 1}{2\sqrt{x^{2} + 1}}} & \text{for } x \geq 0 \\ & \\ -\sqrt{\dfrac{\sqrt{x^{2} + 1} - 1}{2\sqrt{x^{2} + 1}}} & \text{for } x \text{ } 0 \end{array}\right.[/latex]
- [latex]\theta + \sin(2\theta) = \arcsin \left( \dfrac{x}{2} \right) + \dfrac{x\sqrt{4 - x^{2}}}{2}[/latex]
- [latex]\dfrac{1}{2}\theta - \dfrac{1}{2}\sin(2\theta) = \dfrac{1}{2} \arctan \left( \dfrac{x}{7} \right) - \dfrac{7x}{x^{2} + 49}[/latex]
- [latex]4\tan(\theta) - 4\theta = \sqrt{x^{2} - 16} - 4\mbox{arcsec} \left( \dfrac{x}{4} \right)[/latex]
- [latex]\left[-\dfrac{1}{5}, \dfrac{1}{5}\right][/latex]
- [latex]\left[-\dfrac{1}{3}, 1 \right][/latex]
- [latex]\left[-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}\right][/latex]
- [latex](-\infty, -\sqrt{5}] \cup [-\sqrt{3}, \sqrt{3}] \cup [\sqrt{5}, \infty)[/latex]
- [latex](-\infty, \infty)[/latex]
- [latex](-\infty, -3) \cup (-3,3) \cup (3, \infty)[/latex]
- [latex]\left(\dfrac{1}{2}, \infty \right)[/latex]
- [latex]\left[\dfrac{1}{2}, \infty \right)[/latex]
- [latex]\left(-\infty, -\dfrac{1}{12}\right] \cup \left[\dfrac{1}{12}, \infty\right)[/latex]
- [latex](-\infty, -6] \cup [-4, \infty)[/latex]
- [latex](-\infty, -2] \cup [2, \infty)[/latex]
- [latex][0, \infty)[/latex]
- Two cycles of the graph are shown to illustrate the discrepancy discussed. ↵
- Again, we graph two cycles to illustrate the discrepancy discussed. ↵
- This will be the last time we graph two cycles to illustrate the discrepancy discussed. ↵
- The equivalence for [latex]x = \pm 1[/latex] can be verified independently of the derivation of the formula, but Calculus is required to fully understand what is happening at those [latex]x[/latex] values. You'll see what we mean when you work through the details of the identity for [latex]\tan(2t).[/latex] For now, we exclude [latex]x = \pm 1[/latex] from our answer. ↵

