0.6 Basic Inequalities in One Variable
0.6.1 Linear Inequalities
We now turn our attention to linear inequalities. Unlike linear equations which admit at most one solution, the solutions to linear inequalities are generally intervals of real numbers. While the solution strategy for solving linear inequalities is the same as with solving linear equations, we need to remind ourselves that, should we decide to multiply or divide both sides of an inequality by a negative number, we need to reverse the direction of the inequality. In the example below, we work not only some `simple’ linear inequalities in the sense there is only one inequality present, but also some `compound’ linear inequalities which require us to revisit the notions of intersection and union.
Example 0.6.1
Example 0.6.1.1
Solve the following inequalities for the indicated variable.
Solve for ![]() :
: ![]()
Solution:
Solve for ![]() :
: ![]() .
.
We begin by clearing denominators. Then we gather all of the terms containing ![]() to one side of the inequality and put the remaining terms on the other.
to one side of the inequality and put the remaining terms on the other.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{7-8x}{2} & \geq & 4x + 1 & \\ [8pt] 2\left(\dfrac{7-8x}{2}\right) & \geq & 2(4x + 1) & \text{Multiply by $2$} \\ [10pt] \dfrac{\cancel{2}(7-8x)}{\cancel{2}} & \geq & 2(4x) + 2(1) & \text{Distribute} \\ [3pt] 7 - 8x & \geq & 8x + 2 & \\ (7-8x) + 8x-2 & \geq & 8x+2 + 8x -2 & \text{Add $8x$, subtract $2$} \\ 7 - 2 - 8x + 8x & \geq & 8x + 8x + 2 - 2 & \text{Rearrange terms} \\ 5 & \geq & 16x & \text{$8x + 8x = (8+8)x = 16x$} \\ [3pt] \dfrac{5}{16} & \geq & \dfrac{16x}{16} & \text{Divide by the coefficient of $x$} \\[8pt] \dfrac{5}{16} & \geq & x & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-2d6f8eccfef326ec021937d159fb7029_l3.png)
We get ![]() or, said differently,
or, said differently, ![]() . We express this set[1] of real numbers as
. We express this set[1] of real numbers as ![]() .
.
Though not required to do so, we could partially check our answer by substituting ![]() and a few other values in our solution set (
and a few other values in our solution set (![]() , for instance) to make sure the inequality holds. (It also isn’t a bad idea to choose an
, for instance) to make sure the inequality holds. (It also isn’t a bad idea to choose an ![]() , say
, say ![]() , to see that the inequality doesn’t hold there.) The only real way to actually show that our answer works for all values in our solution set is to start with
, to see that the inequality doesn’t hold there.) The only real way to actually show that our answer works for all values in our solution set is to start with ![]() and reverse all of the steps in our solution procedure to prove it is equivalent to our original inequality.
and reverse all of the steps in our solution procedure to prove it is equivalent to our original inequality.
Example 0.6.1.2
Solve the following inequalities for the indicated variable.
Solve for ![]() :
: ![]()
Solution:
Solve for ![]() :
: ![]() .
.
We have our first example of a `compound’ inequality. The solutions to
![]()
must satisfy
![]()
One approach is to solve each of these inequalities separately, then intersect their solution sets. While this method works (and will be used later for more complicated problems), our variable ![]() appears only in the middle expression so we can proceed by working both inequalities at once:
appears only in the middle expression so we can proceed by working both inequalities at once:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{3}{4} \leq & \dfrac{7-y}{2} & < 6 & \\ [10pt] 4\left(\dfrac{3}{4} \right) \leq & 4\left( \dfrac{7-y}{2}\right) & < 4(6) & \text{Multiply by $4$} \\ [12pt] \dfrac{\cancel{4} \cdot 3}{\cancel{4}} \leq & \dfrac{\cancelto{2}{4}(7-y)}{\cancel{2}} & < 24 & \\ [5pt] 3 \leq & 2(7-y) & < 24 & \\ 3 \leq & 2(7)-2y & < 24 & \text{Distrbute}\\ 3 \leq & 14-2y & < 24 & \\ 3 -14 \leq & (14-2y) - 14 & < 24 - 14 & \text{Subtract $14$}\\ -11 \leq & -2y & < 10 & \\ [3pt] \dfrac{-11}{-2} \geq & \dfrac{-2y}{-2} & > \dfrac{10}{-2} & \text{Divide by the coefficient of $y$} \\ [-5pt] & & & \text{Reverse inequalities} \\ [-3pt] \dfrac{11}{2} \geq & y & > -5 & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-51f854ab369f3aee30f78c1d488babbf_l3.png)
Our final answer is ![]() , or, said differently,
, or, said differently, ![]() . In interval notation, this is
. In interval notation, this is ![]() .
.
We could check the reasonableness of our answer as before, and the reader is encouraged to do so.
Example 0.6.1.3
Solve the following inequalities for the indicated variable.
Solve for ![]() :
: ![]()
Solution:
Solve for ![]() :
: ![]() .
.
We have another compound inequality and what distinguishes this one from our previous example is that ![]() appears on both sides of both inequalities. In this case, we need to create two separate inequalities and find all of the real numbers
appears on both sides of both inequalities. In this case, we need to create two separate inequalities and find all of the real numbers ![]() which satisfy both
which satisfy both
![]()
The first inequality,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} 2t-1 &\leq& 4-t \\ 3t &\leq& 5 \\ t \leq \frac{5}{3} \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-72e7a53b83462cd80fc041b95ab5bc18_l3.png)
The second inequality,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} 4-t &<& 6t+1 \\ 3 &<& 7t \\t &>& \frac{3}{7} \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3a175d00b2261bbd0c1d699898e9cb91_l3.png)
Thus our solution is all real numbers ![]() with
with ![]() and
and ![]() , or, writing this as a compound inequality,
, or, writing this as a compound inequality, ![]() . Using interval notation,[2] we express our solution as
. Using interval notation,[2] we express our solution as ![]() .
.
Example 0.6.1.4
Solve the following inequalities for the indicated variable.
Solve for ![]() :
: ![]()
Solution:
Solve for ![]() :
: ![]() .
.
As before, with this inequality we have no choice but to solve each inequality individually and intersect the solution sets. Starting with the leftmost inequality, we first note that in the term ![]() , the vinculum of the square root extends over the
, the vinculum of the square root extends over the ![]() only, meaning the
only, meaning the ![]() is not part of the radicand. In order to avoid confusion, we will write
is not part of the radicand. In order to avoid confusion, we will write ![]() as
as ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 5 + x\sqrt{7} & \leq & 4x+1 & \\ (5 + x\sqrt{7} ) -4x - 5 & \leq& (4x + 1) - 4x - 5 & \text{Subtract $4x$ and $5$} \\ x\sqrt{7} - 4x + 5 - 5 & \leq & 4x - 4x + 1 - 5 & \text{Rearrange terms} \\ x(\sqrt{7} - 4) & \leq & -4 & \text{Factor} \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f9cdb7a87d8396b4adcfb9fd49f110c6_l3.png)
At this point, we need to exercise a bit of caution because the number ![]() is negative.[3]
is negative.[3]
When we divide by it the inequality reverses:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} x(\sqrt{7} - 4) & \leq & -4 & \\[3pt] \dfrac{x(\sqrt{7}-4)}{\sqrt{7}-4} & \geq & \dfrac{-4}{\sqrt{7} - 4} & \text{Divide by the coefficient of $x$} \\ [-8pt] & & & \text{Reverse inequalities} \\ [-3pt] x & \geq & \dfrac{-4}{\sqrt{7} - 4} & \\ [10pt] x & \geq & \dfrac{-4}{-(4 - \sqrt{7})} & \\ [12pt] x & \geq & \dfrac{4}{4 -\sqrt{7}} & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4870b5ad9a1f48448e1569ead9eb3589_l3.png)
We’re only half done because we still have the rightmost inequality to solve.
Fortunately, that one seems rather mundane:
![]()
without too much incident.
Our solution is ![]() and
and ![]() .
.
We may be tempted to write ![]() and call it a day but that would be nonsense! To see why, notice that
and call it a day but that would be nonsense! To see why, notice that ![]() is between
is between ![]() and
and ![]() so
so ![]() is between
is between ![]() and
and ![]() . In particular, we get
. In particular, we get ![]() . On the other hand,
. On the other hand, ![]() . This means that our `solutions’ have to be simultaneously greater than
. This means that our `solutions’ have to be simultaneously greater than ![]() AND less than
AND less than ![]() which is impossible.
which is impossible.
Therefore, this compound inequality has no solution, which means we did all that work for nothing.
Example 0.6.1.5
Solve the following inequalities for the indicated variable.
Solve for ![]() :
: ![]() or
or ![]()
Solution:
Solve for ![]() :
: ![]() or
or ![]() .
.
Our last example is yet another compound inequality but here, instead of the two inequalities being connected with the conjunction `and‘, they are connected with `or‘, which indicates that we need to find the union of the results of each.
Starting with ![]() , we get
, we get ![]() , which gives[4]
, which gives[4] ![]() .
.
The second inequality, ![]() , becomes
, becomes ![]() , which reduces to
, which reduces to ![]() .
.
Our solution set consists of all real numbers ![]() with
with ![]() or
or ![]() . In interval notation, this is
. In interval notation, this is ![]() .
.
0.6.2 Absolute Value Inequalities
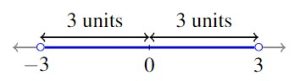
We now turn our attention to solving some basic inequalities involving the absolute value. Suppose we wished to solve ![]() . Geometrically, we are looking for all of the real numbers whose distance from 0 is less than 3 units. We get
. Geometrically, we are looking for all of the real numbers whose distance from 0 is less than 3 units. We get ![]() , or in interval notation,
, or in interval notation, ![]() . Suppose we are asked to solve
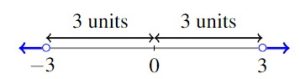
. Suppose we are asked to solve ![]() instead. Now we want the distance between
instead. Now we want the distance between ![]() and
and ![]() to be greater than
to be greater than ![]() units. Moving in the positive direction, this means
units. Moving in the positive direction, this means ![]() . In the negative direction, this puts
. In the negative direction, this puts ![]() . Our solutions would then satisfy
. Our solutions would then satisfy ![]() or
or ![]() . In interval notation, we express this as
. In interval notation, we express this as ![]() .
.
Generalizing this notion, we get the following:
Theorem 0.8 Inequalities Involving Absolute Value
Let ![]() be a real number.
be a real number.
- If
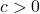 ,
, 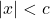 is equivalent to
is equivalent to 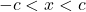 .
. - If
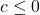 ,
, 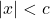 has no solution.
has no solution. - If
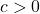 ,
, 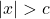 is equivalent to
is equivalent to 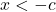 or
or 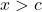 .
. - If
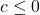 ,
, 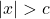 is true for all real numbers.
is true for all real numbers.
If the inequality we’re faced with involves `![]() ‘ or `
‘ or `![]() ,’ we can combine the results of Theorem 0.8 with Theorem 0.4 as needed.
,’ we can combine the results of Theorem 0.8 with Theorem 0.4 as needed.
Strategy for Solving Inequalities Involving Absolute Value
In order to solve an inequality involving the absolute value of a quantity ![]() :
:
- Isolate the absolute value on one side of the inequality.
- Apply Theorem 0.8.
Example 0.6.2
Example 0.6.2.1
Solve the following inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
From Theorem 0.8, ![]() is equivalent to
is equivalent to ![]() or
or ![]() .
.
Solving this compound inequality, we get ![]() or
or ![]() .
.
Our answer, in interval notation, is: ![]() .
.
As with linear inequalities, we can only partially check our answer by selecting values of ![]() both inside and outside of the solution intervals to see which values of
both inside and outside of the solution intervals to see which values of ![]() satisfy the original inequality and which do not.
satisfy the original inequality and which do not.
Example 0.6.2.2
Solve the following inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
Our first step in solving ![]() is to isolate the absolute value.
is to isolate the absolute value.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{4 - 2|2x+1|}{4} & \geq & -\sqrt{3} & \\ [5pt] 4 - 2|2x+1| & \geq & -4\sqrt{3} & \text{Multiply by $4$} \\ - 2|2x+1| & \geq & -4-4\sqrt{3} & \text{Subtract $4$} \\ |2x+1| & \leq & \dfrac{-4-4\sqrt{3}}{-2} & \text{Divide by $-2$, reverse the inequality} \\ [8pt] |2x+1| & \leq & 2 + 2\sqrt{3} & \text{Reduce} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e41ff751d7b73eddd7464367188a6aef_l3.png)
Due to the fact that we’re dealing with `![]() ‘ instead of just `
‘ instead of just `![]() ,’ we can combine Theorems 0.8 and 0.4 to rewrite this last inequality as:[5]
,’ we can combine Theorems 0.8 and 0.4 to rewrite this last inequality as:[5] ![]() .
.
Subtracting the `![]() ‘ across both inequalities gives
‘ across both inequalities gives ![]() , which reduces to
, which reduces to ![]()
In interval notation this reads as ![]() .
.
Example 0.6.2.3
Solve the following inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
There are two absolute values in ![]() , so we cannot directly apply Theorem 0.8 here. Notice, however, that
, so we cannot directly apply Theorem 0.8 here. Notice, however, that ![]() . Using this, we get:
. Using this, we get:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} |2x - 1| & \leq & 3|4 - 8x| - 10 & \\ |2x - 1| & \leq & 3|(-4)(2x-1)| - 10 & \text{Factor}\\ |2x - 1| & \leq & 3|-4||2x-1| - 10 & \text{Product Rule}\\ |2x - 1| & \leq & 12|2x-1| - 10 & \\ -11|2x - 1| & \leq & - 10 & \text{Subtract $12|2x-1|$} \\ |2x - 1| & \geq & \dfrac{10}{11} & \text{Divide by $-11$ and reduce} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9ce772f94a549cb6f03bad5f316785c4_l3.png)
Now we are allowed to invoke Theorems 0.4 and 0.8 and write the equivalent compound inequality: ![]() or
or ![]() .
.
We get ![]() or
or ![]() , which when written with interval notation becomes
, which when written with interval notation becomes ![]() .
.
Example 0.6.2.4
Solve the following inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
The inequality ![]() differs from the previous example in exactly one respect: on the right side of the inequality, we have `
differs from the previous example in exactly one respect: on the right side of the inequality, we have `![]() ‘ instead of `
‘ instead of `![]() .’
.’
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} |2x - 1| & \leq & 3|4 - 8x| + 10 & \\ |2x - 1| & \leq & 3|(-4)(2x-1)| + 10 & \text{Factor}\\ |2x - 1| & \leq & 3|-4||2x-1| + 10 & \text{Product Rule}\\ |2x - 1| & \leq & 12|2x-1| + 10 & \\ -11|2x - 1| & \leq & + 10 & \text{Subtract $12|2x-1|$} \\ |2x - 1| & \geq & -\dfrac{10}{11} & \text{Divide by $-11$ and reduce} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3700b0d59d0939c987b6e6623e25b3e3_l3.png)
The resulting inequality is always true. (Absolute value is, by definition, a distance and hence always ![]() or greater.)
or greater.)
Thus our solution to this inequality is all real numbers.
Example 0.6.2.5
Solve the following inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
To solve ![]() , we rewrite it as the compound inequality:
, we rewrite it as the compound inequality: ![]() and
and ![]() .
.
The first inequality, ![]() , can be re-written as
, can be re-written as ![]() so it is equivalent to
so it is equivalent to ![]() or
or ![]() .
.
Thus the solution to ![]() is
is ![]() or
or ![]() , which in interval notation is
, which in interval notation is ![]() .
.
For ![]() , we combine the results of Theorems 0.4 and 0.8 to get
, we combine the results of Theorems 0.4 and 0.8 to get ![]() so that
so that ![]() , or
, or ![]() .
.
Our solution to ![]() is comprised of values of
is comprised of values of ![]() which satisfy both parts of the inequality, so we intersect
which satisfy both parts of the inequality, so we intersect ![]() with
with ![]() to get our final answer
to get our final answer ![]() .
.
Example 0.6.2.6
Solve the following inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
Our first hope when encountering ![]() is that we can somehow combine the two absolute value quantities as we’d done in earlier examples. We leave it to the reader to show, however, that no matter what we try to factor out of the absolute value quantities, what remains inside the absolute values will always be different.
is that we can somehow combine the two absolute value quantities as we’d done in earlier examples. We leave it to the reader to show, however, that no matter what we try to factor out of the absolute value quantities, what remains inside the absolute values will always be different.
At this point, we take a step back and look at the equation in a more general way: we are adding two absolute values together and wanting the result to be less than or equal to ![]() . The absolute value of anything is always
. The absolute value of anything is always ![]() or greater, so there are no solutions to:
or greater, so there are no solutions to: ![]() .
.
Is it possible that ![]() ? Only if there is an
? Only if there is an ![]() where
where ![]() and
and ![]() at the same time.[6]
at the same time.[6]
The first equation holds only when ![]() , while the second holds only when
, while the second holds only when ![]() . Alas, we have no solution.
. Alas, we have no solution.
The astute reader will have noticed by now that the authors have done nothing in the way of explaining why anyone would ever need to know this stuff. These sections were designed to review skills and concepts that you’ve already learned. Thus, the deeper applications are in the main body of the text as opposed to here in Chapter 0.
We close this section with an example of how the properties in Theorem 0.3 are used in Calculus. Here, `![]() ‘ is the Greek letter `epsilon’ and it represents a positive real number. Those of you who will be taking Calculus in the future should become very familiar with this type of algebraic manipulation.
‘ is the Greek letter `epsilon’ and it represents a positive real number. Those of you who will be taking Calculus in the future should become very familiar with this type of algebraic manipulation.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \left| \dfrac{8-4x}{3} \right| & < & \varepsilon & \\ [12pt] \dfrac{|8 - 4x|}{|3|} & < & \varepsilon & \text{Quotient Rule}\\ [12pt] \dfrac{|-4(x-2)|}{3} & < & \varepsilon & \text{Factor} \\ [12pt] \dfrac{|-4| |x-2|}{3} & < & \varepsilon & \text{Product Rule} \\ [12pt] \dfrac{4 |x-2|}{3} & < & \varepsilon & \\ [12pt] \dfrac{3}{4} \cdot \dfrac{4 |x-2|}{3} & < & \dfrac{3}{4} \cdot \varepsilon & \text{Multiply by $\dfrac{3}{4}$} \\ [12pt] |x -2 | & < & \dfrac{3}{4} \varepsilon & \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-799bba944e66b982e52fb12a70b9ad1a_l3.png)
0.6.3 Section Exercises
In Exercises 1 – 18, solve the given inequality. Write your answer using interval notation.
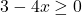
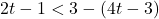
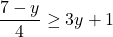
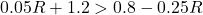
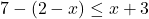
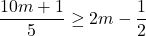
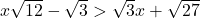
![Rendered by QuickLaTeX.com 2t - 7 \leq \sqrt[3]{18} t](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d143d2f54c6cbacc76ca51933c001225_l3.png)
![Rendered by QuickLaTeX.com 117y \geq y\sqrt{2} - 7y \sqrt[4]{8}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5ab7b545beb61ff075568ef287832340_l3.png)
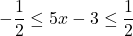
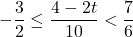
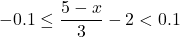
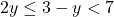
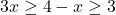
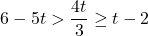
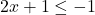 or
or 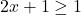
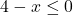 or
or 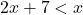
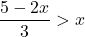 or
or 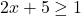
In Exercises 19 – 30, solve the inequality. Write your answer using interval notation.
Section 0.6 Exercise Answers can be found in the Appendix … Coming soon
- Using set-builder notation, our `set' of solutions here is
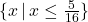 . ↵
. ↵ - If we intersect the solution sets of the two individual inequalities, we get the answer, too:
![Rendered by QuickLaTeX.com \left(-\infty, \frac{5}{3}\right] \cap \left(\frac{3}{7}, \infty\right) = \left( \frac{3}{7}, \frac{5}{3} \right]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ca687dd33aeffcead5a2f0000a989e19_l3.png) . ↵
. ↵ - As a result of
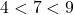 , it stands to reason that
, it stands to reason that 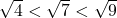 and thus
and thus 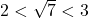 . ↵
. ↵ - Don't forget to change the direction of the inequality! ↵
- Note the use of parentheses:
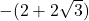 as opposed to
as opposed to 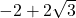 . ↵
. ↵ - Do you see why? ↵

