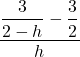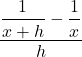3.1 Simplifying Rational Expressions
Before we launch into reviewing the basic arithmetic operations of rational expressions, we take a moment to review how to simplify them properly. As with numeric fractions, we `divide out common factors,’ not common terms. That is, in order to simplify rational expressions, we first factor the numerator and denominator. For example:
![Rendered by QuickLaTeX.com \[ \dfrac{x^4 + 5x^3}{x^3 - 25x} \neq \dfrac{x^4 + 5\cancel{x^3}}{\cancel{x^3} - 25x} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-26c4ec021f64be62569e916eca28410f_l3.png)
but, rather
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{x^4 + 5x^3}{x^3 - 25x} & = & \dfrac{x^3(x + 5)}{x(x^2-25)} & \text{Factor G.C.F.} \\ [12pt] & = & \dfrac{x^3(x + 5)}{x(x-5)(x+5)} & \text{Difference of Squares} \\ [12pt] & = & \dfrac{\cancelto{x^2}{x^3}\cancel{(x + 5)}}{\cancel{x}(x-5)\cancel{(x+5)}} & \text{Divide out the common factors}\\ [12pt] & = & \dfrac{x^2}{x-5} & \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9d134398b79aef7af52829df00e72bb6_l3.png)
This equivalence holds provided the factors being divided aren’t ![]() . A factor of
. A factor of ![]() and a factor of
and a factor of ![]() were divided, thus
were divided, thus ![]() and
and ![]() , so
, so ![]() . We usually stipulate this as:
. We usually stipulate this as:
![]()
While we’re talking about common mistakes, please notice that
![]()
Just like their numeric counterparts, you don’t add algebraic fractions by adding denominators of fractions with common numerators – it’s the other way around:[1]
![]()
It’s time to review the basic arithmetic operations with rational expressions.
Example 3.1.1
Example 3.1.1.1
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
As with numeric fractions, we divide rational expressions by `inverting and multiplying’. Before we get too carried away however, we factor to see what, if any, factors divide out.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{2x^2-5x-3}{x^4 - 4} \div \dfrac{x^2-2x-3}{x^5 + 2x^3} & = & \dfrac{2x^2-5x-3}{x^4 - 4} \cdot \dfrac{x^5 + 2x^3}{x^2-2x-3} & \text{Invert and multiply} \\ [13pt] & = & \dfrac{(2x^2-5x-3)(x^5 + 2x^3)}{(x^4 - 4)(x^2-2x-3)} & \text{Multiply fractions} \\ [13pt] & = & \dfrac{(2x+1)(x-3)x^3(x^2+2)}{(x^2-2)(x^2+2)(x-3)(x+1)} & \text{Factor} \\ [13pt] & = & \dfrac{(2x+1)\cancel{(x-3)}x^3\cancel{(x^2+2)}}{(x^2-2)\cancel{(x^2+2)}\cancel{(x-3)}(x+1)} & \text{divide out common factors} \\ [13pt] & = & \dfrac{x^3(2x+1)}{(x+1)(x^2-2)} & \text{Provided }x \neq 3 \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5e70528774e5af75c56da2b626f811f1_l3.png)
The `![]() ‘ is a result of a factor of
‘ is a result of a factor of ![]() being divided out as we reduced the expression. We also divided out a factor of
being divided out as we reduced the expression. We also divided out a factor of ![]() . Why is there no stipulation as a result of dividing this factor? Because
. Why is there no stipulation as a result of dividing this factor? Because ![]() for all real
for all real ![]() . (See Section 0.5.6 for details.) At this point, we could go ahead and multiply out the numerator and denominator to get
. (See Section 0.5.6 for details.) At this point, we could go ahead and multiply out the numerator and denominator to get
![]()
but for most of the applications where this kind of algebra is needed (solving equations, for instance), it is best to leave the expressions factored. Your instructor will let you know whether to leave your answer in factored form or not.[2]
Example 3.1.1.2
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
As with numeric fractions we need common denominators in order to subtract. This is already the case here so we proceed by subtracting the numerators.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{5}{w^2 - 9} - \dfrac{w+2}{w^2-9} & = & \dfrac{5 - (w+2)}{w^2 - 9}& \text{Subtract fractions}\\ [13pt] & = & \dfrac{5 - w - 2}{w^2-9} & \text{Distribute} \\ [13pt] & = & \dfrac{3-w}{w^2-9} & \text{Combine like terms} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f1edf6df716fc42593f1c3247fdae172_l3.png)
At this point, we need to determine if we can reduce this expression, so we proceed to factor. It first appears as if we have no common factors among the numerator and denominator until we recall the property of `factoring negatives’ from Section 0.1: ![]() . This yields:
. This yields:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{3-w}{w^2-9} & = & \dfrac{-(w-3)}{(w-3)(w+3)} & \text{Factor} \\ [13pt] & = & \dfrac{-\cancel{(w-3)}}{\cancel{(w-3)}(w+3)} & \text{Divide out the common factors} \\ [13pt] & = & \dfrac{-1}{w+3} & \text{Provided $w \neq 3$} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-51e111757c541e7b43150b13a088093f_l3.png)
The stipulation ![]() comes from the division of the
comes from the division of the ![]() factor.
factor.
Example 3.1.1.3
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
In this next example, we are asked to add two rational expressions with different denominators. As with numeric fractions, we must first find a common denominator. To do so, we start by factoring each of the denominators.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{3}{y^2 - 8y + 16} + \dfrac{y+1}{16y - y^3} & = & \dfrac{3}{(y-4)^2} + \dfrac{y+1}{y(16 - y^2)} & \text{Factor} \\ [13pt] & = & \dfrac{3}{(y-4)^2} + \dfrac{y+1}{y(4-y)(4+y)} & \text{Factor some more} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c204278c808b0a8983886e62acc9d6fa_l3.png)
To find the common denominator, we examine the factors in the first denominator and note that we need a factor of ![]() . We now look at the second denominator to see what other factors we need. We need a factor of
. We now look at the second denominator to see what other factors we need. We need a factor of ![]() and
and ![]() . What about
. What about ![]() ? As mentioned in the last example, we can factor this as:
? As mentioned in the last example, we can factor this as: ![]() . Using properties of negatives, we `migrate’ this negative out to the front of the fraction, turning the addition into subtraction. We find the (least) common denominator to be
. Using properties of negatives, we `migrate’ this negative out to the front of the fraction, turning the addition into subtraction. We find the (least) common denominator to be ![]() . We can now proceed to multiply the numerator and denominator of each fraction by whatever factors are missing from their respective denominators to produce equivalent expressions with common denominators.
. We can now proceed to multiply the numerator and denominator of each fraction by whatever factors are missing from their respective denominators to produce equivalent expressions with common denominators.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{3}{(y-4)^2} + \dfrac{y+1}{y(4-y)(4+y)} & = & \dfrac{3}{(y-4)^2} + \dfrac{y+1}{y(-(y-4))(y+4)} & \\ [8pt] & = & \dfrac{3}{(y-4)^2} - \dfrac{y+1}{y(y-4)(y+4)} & \\ [10pt] & = & \dfrac{3}{(y-4)^2} \cdot \dfrac{y(y+4)}{y(y+4)} - \dfrac{y+1}{y(y-4)(y+4)} \cdot \dfrac{(y-4)}{(y-4)} & \text{Equivalent} \\[-8pt] & & & \text{Fractions} \\ & = & \dfrac{3y(y+4)}{(y-4)^2y(y+4)} - \dfrac{(y+1)(y-4)}{y(y-4)^2(y+4)} & \text{Multiply} \\ [-8pt] & & & \text{Fractions} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-776c9832798aeca9c159197e21f77c95_l3.png)
At this stage, we can subtract numerators and simplify. We’ll keep the denominator factored (in case we can reduce down later), but in the numerator, as there are no common factors, we proceed to perform the indicated multiplication and combine like terms.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{3y(y+4)}{(y-4)^2y(y+4)} - \dfrac{(y+1)(y-4)}{y(y-4)^2(y+4)} & = & \dfrac{3y(y+4) -(y+1)(y-4)}{(y-4)^2y(y+4)} & \text{Subtract numerators} \\ [10pt] & = & \dfrac{3y^2 + 12y - (y^2 - 3y - 4)}{(y-4)^2 y (y+4)} & \text{Distribute} \\ [10pt] & = & \dfrac{3y^2 + 12y - y^2 + 3y + 4}{(y-4)^2 y (y+4)} & \text{Distribute} \\ [10pt] & = & \dfrac{2y^2 + 15y + 4}{y (y+4) (y-4)^2} & \text{Gather like terms} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c9bdabf5a8651224f7daa2f3e3b8b368_l3.png)
We would like to factor the numerator and divide out factors it has in common with the denominator. After a few attempts, it appears as if the numerator doesn’t factor, at least over the integers. As a check, we compute the discriminant of ![]() and get
and get ![]() . This isn’t a perfect square so we know that the quadratic equation
. This isn’t a perfect square so we know that the quadratic equation ![]() has irrational solutions. This means
has irrational solutions. This means ![]() can’t factor over the integers[3] so we are done.
can’t factor over the integers[3] so we are done.
Example 3.1.1.4
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
At first glance, it doesn’t seem as if there is anything that can be done with ![]() because the exponents on the variables are different. However, the exponents are negative, so these are actually rational expressions. In the first term, the
because the exponents on the variables are different. However, the exponents are negative, so these are actually rational expressions. In the first term, the ![]() exponent applies to the
exponent applies to the ![]() only but in the second term, the exponent
only but in the second term, the exponent ![]() applies to both the
applies to both the ![]() and the
and the ![]() , as indicated by the parentheses. One way to proceed is as follows:
, as indicated by the parentheses. One way to proceed is as follows:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 2t^{-3} - (3t)^{-2} & = & \dfrac{2}{t^3} - \dfrac{1}{(3t)^2} & \\ [10pt] & = & \dfrac{2}{t^3} - \dfrac{1}{9t^2} & \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-cb2fa7e208cf3c3bbfd80c61c3a9853a_l3.png)
We see that we are being asked to subtract two rational expressions with different denominators, so we need to find a common denominator. The first fraction contributes a ![]() to the denominator, while the second contributes a factor of
to the denominator, while the second contributes a factor of ![]() . Thus our common denominator is
. Thus our common denominator is ![]() , so we are missing a factor of `
, so we are missing a factor of `![]() ‘ in the first denominator and a factor of `
‘ in the first denominator and a factor of `![]() ‘ in the second.
‘ in the second.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{2}{t^3} - \dfrac{1}{9t^2} & = & \dfrac{2}{t^3} \cdot \dfrac{9}{9} - \dfrac{1}{9t^2} \cdot \dfrac{t}{t} & \text{Equivalent Fractions} \\ [10pt] & = & \dfrac{18}{9t^3} - \dfrac{t}{9t^3} & \text{Multiply}\\ [10pt] & = & \dfrac{18 - t}{9t^3} & \text{Subtract} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d1bd38b1e1ef410561570c1275470a8c_l3.png)
We find no common factors among the numerator and denominator, so we are done.
A second way to approach this problem is by factoring. We can extend the concept of the `Polynomial G.C.F.’ to these types of expressions and we can follow the same guidelines as set forth in Section 0.3 to factor out the G.C.F. of these two terms. The key ideas to remember are that we take out each factor with the smallest exponent and that factoring is the same as dividing. We first note that ![]() and we see that the smallest power on
and we see that the smallest power on ![]() is
is ![]() . Thus we want to factor out
. Thus we want to factor out ![]() from both terms. It’s clear that this will leave
from both terms. It’s clear that this will leave ![]() in the first term, but what about the second term? As factoring is the same as dividing, we would be dividing the second term by
in the first term, but what about the second term? As factoring is the same as dividing, we would be dividing the second term by ![]() which thanks to the properties of exponents is the same as multiplying by
which thanks to the properties of exponents is the same as multiplying by ![]() . The same holds for
. The same holds for ![]() . Even though there are no factors of
. Even though there are no factors of ![]() in the first term, we can factor out
in the first term, we can factor out ![]() by multiplying it by
by multiplying it by ![]() . We put these ideas together below.
. We put these ideas together below.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 2t^{-3} - (3t)^{-2} & = & 2t^{-3} - 3^{-2} t^{-2} & \text{Properties of Exponents} \\ [5pt] & = & 3^{-2} t^{-3} (2(3)^2 - t^{1}) & \text{Factor} \\ [5pt] & = & \dfrac{1}{3^2} \dfrac{1}{t^3} (18 - t) & \text{Rewrite}\\ [10pt] & = & \dfrac{18-t}{9t^3} & \text{Multiply} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e565a8aa55f14375a06c85925b03eaf5_l3.png)
While both ways are valid, one may be more of a natural fit than the other depending on the circumstances and temperament of the student.
Example 3.1.1.5
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
As with the previous example, we show two different yet equivalent ways to approach simplifying ![]() . First up is what we’ll call the `common denominator approach’ where we rewrite the negative exponents as fractions and proceed from there.
. First up is what we’ll call the `common denominator approach’ where we rewrite the negative exponents as fractions and proceed from there.
- Common Denominator Approach:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 10x(x-3)^{-1} + 5x^2(-1)(x-3)^{-2} & = & \dfrac{10x}{x-3} + \dfrac{5x^2(-1)}{(x-3)^2} & \\ [10pt] & = & \dfrac{10x}{x-3} \cdot \dfrac{x-3}{x-3} - \dfrac{5x^2}{(x-3)^2} & \text{Equivalent Fractions} \\ [10pt] & = & \dfrac{10x(x-3)}{(x-3)^2} - \dfrac{5x^2}{(x-3)^2} & \text{Multiply} \\ [10pt] & = & \dfrac{10x(x-3) - 5x^2}{(x-3)^2} & \text{Subtract} \\ [10pt] & = & \dfrac{5x(2(x-3) - x)}{(x-3)^2} & \text{Factor out G.C.F.} \\ [10pt] & = & \dfrac{5x(2x-6-x)}{(x-3)^2} & \text{Distribute} \\ [10pt] & = & \dfrac{5x(x-6)}{(x-3)^2} & \text{Combine like terms} \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d5525059ac3abbabc421cb51f54a6a85_l3.png)
Both the numerator and the denominator are completely factored with no common factors so we are done.
- Factoring Approach: In this case, the G.C.F. is
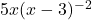 . Factoring this out of both terms gives:
. Factoring this out of both terms gives:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 10x(x-3)^{-1} + 5x^2(-1)(x-3)^{-2} & = & 5x(x-3)^{-2}(2(x-3)^{1} - x) & \text{Factor} \\ [8pt] & = & \dfrac{5x}{(x-3)^2} (2x-6 - x) & \text{Rewrite, distribute}\\ [12pt] & = & \dfrac{5x(x-6)}{(x-3)^2} & \text{Multiply}\\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-0cad5f767831febee1c1bc12af555291_l3.png)
As expected, we got the same reduced fraction as before.
3.1.1 Difference Quotients
Recall in Section 1.3.4 the concept of the average rate of change of a function over the interval ![]() is the slope between the two points
is the slope between the two points ![]() and
and ![]() and is given by
and is given by
![]()
Consider a function ![]() defined over an interval containing
defined over an interval containing ![]() and
and ![]() where
where ![]() . The average rate of change of
. The average rate of change of ![]() over the interval
over the interval ![]() is thus given by the formula:[4]
is thus given by the formula:[4]
![]()
The above is an example of what is traditionally called the difference quotient or Newton quotient of ![]() , as it is the quotient of two differences, namely
, as it is the quotient of two differences, namely ![]() and
and ![]() . Another formula for the difference quotient keeps with the notation
. Another formula for the difference quotient keeps with the notation ![]() instead of
instead of ![]() :
:
![]()
It is important to understand that in this formulation of the difference quotient, the variables `![]() ‘ and `
‘ and `![]() ‘ are distinct – that is they do not combine as like terms.
‘ are distinct – that is they do not combine as like terms.
In Section 3.2, the average rate of change of position function ![]() can be interpreted as the average velocity (see Definition 3.5.) We can likewise re-cast this definition. After relabeling
can be interpreted as the average velocity (see Definition 3.5.) We can likewise re-cast this definition. After relabeling ![]() , we get
, we get
![]()
which measures the average velocity between time ![]() and time
and time ![]() as a function of
as a function of ![]() .
.
Note that, regardless of which form the difference quotient takes, when ![]() ,
, ![]() , or
, or ![]() is
is ![]() , the difference quotient returns the indeterminant form `
, the difference quotient returns the indeterminant form `![]() .’ As we will see with rational functions in Section 3.2, when this happens, we can reduce the fraction to lowest terms to see if we have a vertical asymptote or hole in the graph. With this in mind, when we speak of `simplifying the difference quotient,’ we mean to manipulate the expression until the factor of `
.’ As we will see with rational functions in Section 3.2, when this happens, we can reduce the fraction to lowest terms to see if we have a vertical asymptote or hole in the graph. With this in mind, when we speak of `simplifying the difference quotient,’ we mean to manipulate the expression until the factor of `![]() ‘ or `
‘ or `![]() ‘ divides out from the denominator.
‘ divides out from the denominator.
Our next example invites us to simplify three difference quotients, each cast slightly differently. In each case, the bulk of the work involves algebra. We refer the reader Section 0.2 for additional review, if needed.
Example 3.1.2
Example 3.1.2.1a
Compute and simplify the indicated difference quotients for the following functions:
For ![]() , compute and simplify:
, compute and simplify:
![]()
Solution:
For ![]() , compute and simplify
, compute and simplify ![]() .
.
For our first difference quotient, we find ![]() by substituting the quantity
by substituting the quantity ![]() in for
in for ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} f(3+h) & = & (3+h)^2 - (3+h) -2 & \\ & = & 9 + 6h+h^2 - 3 - h -2 & \\ & = & 4 + 5h + h^2 & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7dfdb612e1dcf3d6a6e0d333de19f707_l3.png)
![]() , so the difference quotient can be rewritten as:
, so the difference quotient can be rewritten as:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{f(3+h)-f(3)}{h} & = & \dfrac{(4 + 5h + h^2) -4}{h} & \\ & = & \dfrac{5h+h^2}{h} & \\ & = & \dfrac{h(5+h)}{h} & \text{factor} \\ & = & \dfrac{\cancel{h}(5+h)}{\cancel{h}} & \text{divide out } h \\[6pt] & = & 5+h \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9e13453c511c16ff57ad32956cf67d74_l3.png)
Example 3.1.2.1b
Compute and simplify the indicated difference quotients for the following functions:
For ![]() , compute and simplify:
, compute and simplify:
![]()
Solution:
For ![]() , compute and simplify
, compute and simplify ![]() .
.
For the second difference quotient, we first find ![]() . We replace every occurrence of
. We replace every occurrence of ![]() in the formula
in the formula ![]() with the quantity
with the quantity ![]() to get
to get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} f(x+h) & = & (x+h)^2 - (x+h) -2 & \\ [8pt] & = & x^2 + 2xh + h^2 - x - h - 2. \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-21315c8a60e6b153febce374a6b1e432_l3.png)
So the difference quotient is
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{f(x+h)-f(x)}{h} & = & \dfrac{\left(x^2+2xh+h^2-x-h-2 \right)-\left(x^{2}-x-2 \right)}{h} & \\[8pt] & = & \dfrac{x^2+2xh+h^2-x-h-2-x^2+x+2}{h} & \\ [8pt] & = & \dfrac{2xh+h^2-h}{h} & \\ [8pt] & = & \dfrac{h \left(2x+h-1\right)}{h} & \text{factor} \\ [8pt] & = & \dfrac{\cancel{h} \left(2x+h-1\right)}{\cancel{h}} & \text{divide out } h \\ [8pt] & = & 2x+h-1 \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3896cc036462253b54c4dc1e43062ca3_l3.png)
Note if we substitute ![]() into this expression, we obtain
into this expression, we obtain ![]() which agrees with our answer from the first difference quotient.
which agrees with our answer from the first difference quotient.
Example 3.1.2.2a
Compute and simplify the indicated difference quotients for the following functions:
For ![]() , compute and simplify:
, compute and simplify:
![]()
Solution:
For ![]() , compute and simplify
, compute and simplify ![]() .
.
Rewriting ![]() , we see the first expression really is a difference quotient:
, we see the first expression really is a difference quotient:
![]()
![]() and
and ![]() , so our difference quotient is:
, so our difference quotient is:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{g(0+\Delta x)-g(0)}{\Delta x} & = & \dfrac{\dfrac{3}{2\Delta x+1}-3}{\Delta x} & \\ [10pt] & = & \dfrac{\dfrac{3}{2\Delta x+1}-3}{\Delta x} \cdot \dfrac{(2\Delta x+1)}{(2\Delta x+1)} & \\ [10pt] & = & \dfrac{3-3(2\Delta x+1)}{\Delta x(2\Delta x+1)} & \\ [10pt] & = & \dfrac{3 - 6 \Delta x - 3}{\Delta x(2\Delta x+1)} & \\ [10pt] & = & \dfrac{-6\Delta x}{\Delta x(2\Delta x+1)} & \\ [10pt] & = & \dfrac{-6\cancel{\Delta x}}{\cancel{\Delta x}(2\Delta x+1)} & \\ [10pt] & = & \dfrac{-6}{2\Delta x+1} & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9514474cd9ec56c00a23932a80236f53_l3.png)
Example 3.1.2.2b
Compute and simplify the indicated difference quotients for the following functions:
For ![]() , compute and simplify:
, compute and simplify:
![]()
Solution:
For ![]() , compute and simplify
, compute and simplify ![]() .
.
For our next difference quotient, we first find ![]() by replacing every occurrence of
by replacing every occurrence of ![]() in the formula for
in the formula for ![]() with the quantity
with the quantity ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} g(x+\Delta x) & = & \dfrac{3}{2(x+\Delta x)+1} & \\ & = & \dfrac{3}{2x+2\Delta x+1}. \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c087127f8a90f9218a04168494047b65_l3.png)
Hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{g(x+\Delta x)-g(x)}{\Delta x} & = & \dfrac{\dfrac{3}{2x+2\Delta x+1}-\dfrac{3}{2x+1}}{\Delta x} & \\ [10pt] & = & \dfrac{\dfrac{3}{2x+2\Delta x+1}-\dfrac{3}{2x+1}}{\Delta x} \cdot \dfrac{(2x+2\Delta x+1)(2x+1)}{(2x+2\Delta x+1)(2x+1)} & \\ [10pt] & = & \dfrac{3(2x+1)-3(2x+2\Delta x+1)}{\Delta x(2x+2\Delta x+1)(2x+1)} & \\ [10pt] & = & \dfrac{6x+3-6x-6\Delta x-3}{\Delta x(2x+2\Delta x+1)(2x+1)} & \\ [10pt] & = & \dfrac{-6\Delta x}{\Delta x(2x+2\Delta x+1)(2x+1)} & \\ [10pt] & = & \dfrac{-6\cancel{\Delta x}}{\cancel{\Delta x}(2x+2\Delta x+1)(2x+1)} & \\ [10pt] & = & \dfrac{-6}{(2x+2\Delta x+1)(2x+1)} & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a25cd60d049782f438b7750c03059bad_l3.png)
We have managed to divide the factor `![]() ‘ from the denominator, therefore we are done. Substituting
‘ from the denominator, therefore we are done. Substituting ![]() into our final expression gives
into our final expression gives ![]() , thus checking our previous answer.
, thus checking our previous answer.
Example 3.1.2.3a
Compute and simplify the indicated difference quotients for the following functions:
For ![]() , compute and simplify:
, compute and simplify:
![]()
Solution:
For ![]() , compute and simplify
, compute and simplify ![]() .
.
We start with ![]() and
and ![]() and get:
and get:
![]()
In order to divide out the factor `![]() ‘ from the denominator, we set about rationalizing the numerator by multiplying both numerator and denominator by the conjugate of the numerator,
‘ from the denominator, we set about rationalizing the numerator by multiplying both numerator and denominator by the conjugate of the numerator, ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcll} \dfrac{r(9+\Delta t) - r(9)}{\Delta t} & = & \dfrac{\sqrt{9+\Delta t} - 3}{\Delta t} & \\ [20pt] & = & \dfrac{\left(\sqrt{9+\Delta t} - 3 \right)}{\Delta t} \cdot \dfrac{\left(\sqrt{9+\Delta t} + 3\right)}{\left(\sqrt{9+\Delta t} + 3\right)} & \text{Multiply by the conjugate.} \\[20pt] & = & \dfrac{\left(\sqrt{9+\Delta t}\right)^2 -(3)^2}{\Delta t\left(\sqrt{9+\Delta t} + 3\right)} & \text{Difference of Squares.}\\ [20pt] & = & \dfrac{(9+\Delta t) - 9}{\Delta t\left(\sqrt{9+\Delta t} + 3\right)} & \\ [20pt] & = & \dfrac{\Delta t}{\Delta t\left(\sqrt{9+\Delta t} + 3\right)} & \\ [20pt] & = & \dfrac{\cancelto{1}{\Delta t}}{\cancel{\Delta t}\left(\sqrt{9+\Delta t} + 3\right)} & \\ [20pt] & = & \dfrac{1}{\sqrt{9+\Delta t} +3} & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-322993b59c390dd2faea877dadb7531c_l3.png)
Example 3.1.2.3b
Compute and simplify the indicated difference quotients for the following functions:
For ![]() , compute and simplify:
, compute and simplify:
![]()
Solution:
For ![]() , compute and simplify
, compute and simplify ![]() .
.
As one might expect, we use the same strategy to simplify our final different quotient. We have:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcll} \dfrac{r(t+\Delta t) - r(t)}{\Delta t} & = & \dfrac{\sqrt{t+\Delta t} - \sqrt{t}}{\Delta t} & \\ [20pt] & = & \dfrac{\left(\sqrt{t+\Delta t} - \sqrt{t}\right)}{\Delta t} \cdot \dfrac{\left(\sqrt{t+\Delta t} + \sqrt{t}\right)}{\left(\sqrt{t+\Delta t} + \sqrt{t}\right)} & \text{Multiply by the conjugate.} \\ [20pt] & = & \dfrac{\left(\sqrt{t+\Delta t}\right)^2 - \left(\sqrt{t}\right)^2}{\Delta t\left(\sqrt{t+\Delta t} + \sqrt{t}\right)} & \text{Difference of Squares.}\\ [20pt] & = & \dfrac{(t+\Delta t) - t}{\Delta t\left(\sqrt{t+\Delta t} + \sqrt{t}\right)} & \\ [20pt] & = & \dfrac{\Delta t}{\Delta t\left(\sqrt{t+\Delta t} + \sqrt{t}\right)} & \\ [20pt] & = & \dfrac{\cancelto{1}{\Delta t}}{\cancel{\Delta t}\left(\sqrt{t+\Delta t} + \sqrt{t}\right)} & \\ [20pt] & = & \dfrac{1}{\sqrt{t+\Delta t} + \sqrt{t}} & \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-843b53fb37113bec25061f01e83efcf1_l3.png)
We have divided the original `![]() ‘ factor from the denominator, thus we are done. Setting
‘ factor from the denominator, thus we are done. Setting ![]() in this expression, we get
in this expression, we get ![]() which agrees with our previous answer.
which agrees with our previous answer.
We close this section with an application.
Example 3.1.3
Example 3.1.3.1
Let ![]() ,
, ![]() give the height of a model rocket above the Moon’s surface, in feet,
give the height of a model rocket above the Moon’s surface, in feet, ![]() seconds after liftoff.
seconds after liftoff.
Compute and simplify: ![]() , for
, for ![]() .
.
Solution:
Compute and simplify: ![]() , for
, for ![]() .
.
To find ![]() , we first find
, we first find ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} s(15+\Delta t) & = & -5(15+\Delta t)^2 + 100(15+\Delta t) & \\ & = & -5(225+30 \Delta t + (\Delta t)^2) + 1500 + 100 \Delta t& \\ & = & -5(\Delta t)^2 -50 \Delta t +375 & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-92f9cf9e6b84c07c82454efc1aa6e2ea_l3.png)
![]() , giving us:
, giving us:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \overline{v}(\Delta t)& = & \dfrac{s(15+ \Delta t) - s(15)}{\Delta t} & \\ [7pt] & = & \dfrac{(-5(\Delta t)^2-50 \Delta t + 375) - 375}{\Delta t} & \\ [7pt] & = & \dfrac{\Delta t (-5 \Delta t - 50)}{\Delta t} & \\ [7pt] & = & \dfrac{\cancel{\Delta} t (-5 \Delta t - 50)}{\cancel{\Delta t}} & \\ [7pt] & = & -5 \Delta t - 50 & \text{$\Delta t \neq 0$} \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b07df8fff8d1a4e2c06b7c5a4aa87c14_l3.png)
In addition to the restriction ![]() , we also know the domain of
, we also know the domain of ![]() is
is ![]() . Hence, we also require
. Hence, we also require ![]() or
or ![]() .
.
Our final answer is ![]() , for
, for ![]()
Example 3.1.3.2
Let ![]() ,
, ![]() give the height of a model rocket above the Moon’s surface, in feet,
give the height of a model rocket above the Moon’s surface, in feet, ![]() seconds after liftoff.
seconds after liftoff.
Determine and interpret ![]() .
.
Solution:
Determine and interpret ![]() . \vskip 0.15em
. \vskip 0.15em
We find ![]() .
.
This means the average velocity over between time ![]() seconds and
seconds and ![]() seconds is
seconds is ![]() feet per second. This indicates the rocket is, on average, heading downwards at a rate of
feet per second. This indicates the rocket is, on average, heading downwards at a rate of ![]() feet per second.
feet per second.
Example 3.1.3.3
Let ![]() ,
, ![]() give the height of a model rocket above the Moon’s surface, in feet,
give the height of a model rocket above the Moon’s surface, in feet, ![]() seconds after liftoff.
seconds after liftoff.
Graph ![]() .
.
Solution:
Graph ![]() .
.
The graph of ![]() is a line with slope
is a line with slope ![]() and
and ![]() -intercept
-intercept ![]() . However, as the domain of
. However, as the domain of ![]() is
is ![]() , the graph of
, the graph of ![]() is a line segment from
is a line segment from ![]() to
to ![]() with a hole at
with a hole at ![]() .
.

Example 3.1.3.4
Let ![]() ,
, ![]() give the height of a model rocket above the Moon’s surface, in feet,
give the height of a model rocket above the Moon’s surface, in feet, ![]() seconds after liftoff.
seconds after liftoff.
Describe the behavior of ![]() as
as ![]() and interpret.
and interpret.
Solution:
Describe the behavior of ![]() as
as ![]() and interpret.
and interpret.
As ![]() ,
, ![]() meaning as we approach
meaning as we approach ![]() , the velocity of the rocket approaches
, the velocity of the rocket approaches ![]() feet per second. That is,
feet per second. That is, ![]() seconds after lift-off, the rocket is heading back towards the surface of the moon at a rate of
seconds after lift-off, the rocket is heading back towards the surface of the moon at a rate of ![]() feet per second.
feet per second.
The reader is invited to compare Example 3.2.3 in Section 3.2 with Example 3.1.3 above. We obtain the exact same information because we are asking the exact same questions – they are just framed differently.
3.1.2 Section Exercises
In Exercises 1 – 18, perform the indicated operations and simplify.
In Exercises 19 – 28, find and simplify the difference quotients:
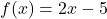
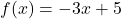
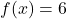
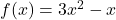
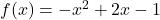
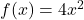
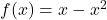
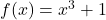
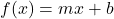 where
where 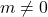
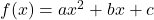 where
where 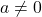
In Exercises 29 – 36, find and simplify the difference quotients:
In Exercises 37 – 43, find and simplify the difference quotients:
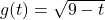

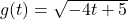
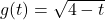
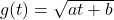 , where
, where 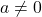 .
.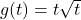
![Rendered by QuickLaTeX.com g(t) = \sqrt[3]{t}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7c7e24d89d18511552e695969d277dde_l3.png) HINT:
HINT: 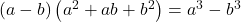
- In this exercise, we explore decomposing a function into its positive and negative parts. Given a function
 , we define the positive part of
, we define the positive part of  , denoted
, denoted 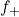 and negative part of
and negative part of  , denoted
, denoted 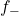 by:
by:
![Rendered by QuickLaTeX.com \[ f_{+}(x) = \dfrac{f(x) + |f(x)|}{2}, \qquad \text{and} \qquad f_{-}(x) = \dfrac{f(x) - |f(x)|}{2}. \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-386ab1a8e9037a862f9b3bac80185617_l3.png)
- Graph each of the functions
 below along with
below along with 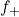 and
and 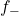 .
.
Why is
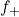 called the `positive part’ of
called the `positive part’ of  and
and 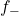 called the `negative part’ of
called the `negative part’ of  ?
? - Show that
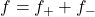 .
. - Use Definition 1.12 to rewrite the expressions for
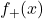 and
and 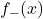 as piecewise defined functions.
as piecewise defined functions.
- Graph each of the functions
Section 3.1 Exercise Answers can be found in the Appendix … Coming soon
- One of the most common errors students make on college Mathematics placement tests is that they forget how to add algebraic fractions correctly. This places many students into remedial classes even though they are probably ready for college-level Math. We urge you to really study this section with great care so that you don't fall into that trap. ↵
- Speaking of factoring, do you remember why
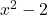 can't be factored over the integers? ↵
can't be factored over the integers? ↵ - See the remarks following Theorem 0.6. ↵
- assuming
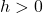 ; otherwise, we the interval is
; otherwise, we the interval is ![Rendered by QuickLaTeX.com [x+h, x]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3d6790477ffcb4cdc4cc21531880a99e_l3.png) . We get the same formula for the difference quotient either way. ↵
. We get the same formula for the difference quotient either way. ↵
The average rate of change for f(x) between a point (x,f(x)) and a point (x+h, f(x+h)) on the curve.