4.1 Properties of Root Functions and Their Graphs
4.1.1 Root Functions
As with polynomial functions and rational functions, we begin our study of functions involving radicals with a special family of functions: the (principal) root functions.
Definition 4.1
Let ![]() with
with ![]() . The
. The ![]() th (principal) root function is the function
th (principal) root function is the function ![]() .
.
NOTE: If ![]() is even, the domain of
is even, the domain of ![]() is
is ![]() ; if
; if ![]() is odd, the domain of
is odd, the domain of ![]() is
is ![]() .
.
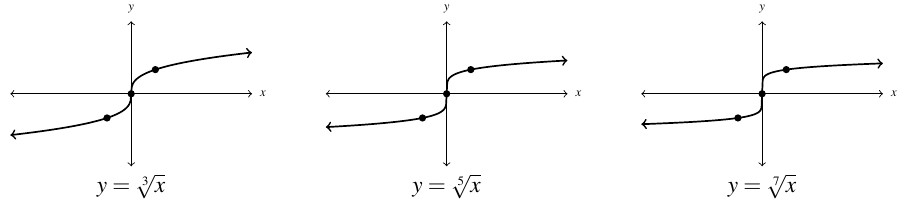
The domain restriction for even indexed roots means that, once again, we are restricting our attention to real numbers.[1] We graph a few members of the root function family below, and quickly notice that, as with the monomial, and, more generally, the Laurent monomial functions, the behavior of the root functions depends primarily on whether the root is even or odd.
In addition to having the common domain of ![]() , the graphs of
, the graphs of ![]() for even indices,
for even indices, ![]() , all share the points
, all share the points ![]() and
and ![]() . As
. As ![]() increases, the functions become `steeper’ near the
increases, the functions become `steeper’ near the ![]() -axis and `flatter’ as
-axis and `flatter’ as ![]() . To show
. To show ![]() as
as ![]() , we show, more generally, the range of
, we show, more generally, the range of ![]() is
is ![]() . Indeed, if
. Indeed, if ![]() is a real number, then
is a real number, then ![]() so
so ![]() is in the range of
is in the range of ![]() . Note that
. Note that ![]() is increasing: that is, if
is increasing: that is, if ![]() , then
, then ![]() . This property is useful in solving certain types of polynomial inequalities.[2]
. This property is useful in solving certain types of polynomial inequalities.[2]

The functions ![]() for odd natural numbers,
for odd natural numbers, ![]() , also follow a predictable trend – steepening near
, also follow a predictable trend – steepening near ![]() and flattening as
and flattening as ![]() . The range for these functions is
. The range for these functions is ![]() because if
because if ![]() is any real number,
is any real number, ![]() , so
, so ![]() is in the range of
is in the range of ![]() . Like the even indexed roots, the odd indexed roots are also increasing. Moreover, these graphs appear to be symmetric about the origin. Sure enough, when
. Like the even indexed roots, the odd indexed roots are also increasing. Moreover, these graphs appear to be symmetric about the origin. Sure enough, when ![]() is odd,
is odd, ![]() so
so ![]() is an odd function.
is an odd function.
At this point, you’re probably expecting a theorem like Theorems 1.4, 2.1, 2.2, 3.1 – that is, a theorem which tells us how to obtain the graph of ![]() from the graph of
from the graph of ![]() – and you would not be wrong. Here, however, we need to add an extra parameter `
– and you would not be wrong. Here, however, we need to add an extra parameter `![]() ‘ to the recipe and discuss functions of the form
‘ to the recipe and discuss functions of the form ![]() . The reason is that, with all of the previous function families, we were always able to factor out the coefficient of
. The reason is that, with all of the previous function families, we were always able to factor out the coefficient of ![]() . We list some examples of this below, and invite the reader to revisit other examples in the text:
. We list some examples of this below, and invite the reader to revisit other examples in the text:
For a function like ![]() , this approach works fine. However, if the coefficient of
, this approach works fine. However, if the coefficient of ![]() is negative, for example,
is negative, for example, ![]() we get stuck the product rule for radicals doesn’t extend to negative quantities when the index is even.[3] Hence we add an extra parameter which means we have an extra step. We state Theorem 4.1 below.
we get stuck the product rule for radicals doesn’t extend to negative quantities when the index is even.[3] Hence we add an extra parameter which means we have an extra step. We state Theorem 4.1 below.
Theorem 4.1
For real numbers ![]() ,
, ![]() ,
, ![]() , and
, and ![]() with
with ![]() , the graph of
, the graph of ![]() can be obtained from the graph of
can be obtained from the graph of ![]() by performing the following operations, in sequence:
by performing the following operations, in sequence:
- add
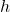 to each of the
to each of the 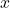 -coordinates of the points on the graph of
-coordinates of the points on the graph of  . This results in a horizontal shift to the right if
. This results in a horizontal shift to the right if 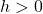 or left if
or left if 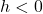 .
.
NOTE: This transforms the graph of![Rendered by QuickLaTeX.com y = \sqrt[n]{x}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-971585c308a087c2cf47a63a9a4a3204_l3.png) to
to ![Rendered by QuickLaTeX.com y = \sqrt[n]{x-h}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8c3813859176fcdfb4b78517878295d0_l3.png) .
. - divide the
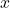 -coordinates of the points on the graph obtained in Step 1 by
-coordinates of the points on the graph obtained in Step 1 by 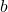 . This results in a horizontal scaling, but may also include a reflection about the
. This results in a horizontal scaling, but may also include a reflection about the 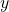 -axis if
-axis if 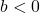 .
.
NOTE: This transforms the graph of![Rendered by QuickLaTeX.com y = \sqrt[n]{x-h}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8c3813859176fcdfb4b78517878295d0_l3.png) to
to ![Rendered by QuickLaTeX.com y = \sqrt[n]{bx-h}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6fad93e0689df48fcf6eb8a758475849_l3.png) .
. - multiply the
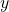 -coordinates of the points on the graph obtained in Step 2 by
-coordinates of the points on the graph obtained in Step 2 by  . This results in a vertical scaling, but may also include a reflection about the
. This results in a vertical scaling, but may also include a reflection about the 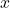 -axis if
-axis if 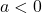 .
.
NOTE: This transforms the graph of![Rendered by QuickLaTeX.com y = \sqrt[n]{bx-h}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6fad93e0689df48fcf6eb8a758475849_l3.png) to
to ![Rendered by QuickLaTeX.com y = a\sqrt[n]{bx-h}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-0f741f4a7d96fafe64d9c5c756784d9b_l3.png) .
. - add
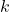 to each of the
to each of the 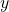 -coordinates of the points on the graph obtained in Step 3. This results in a vertical shift up if
-coordinates of the points on the graph obtained in Step 3. This results in a vertical shift up if 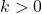 or down if
or down if 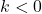 .
.
NOTE: This transforms the graph of![Rendered by QuickLaTeX.com y = a\sqrt[n]{bx-h}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-0f741f4a7d96fafe64d9c5c756784d9b_l3.png) to
to ![Rendered by QuickLaTeX.com y = a\sqrt[n]{bx-h} + k](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-12d8ab85975c529aa0cd8621517cc596_l3.png) .
.
Proof. As usual, we `build’ the graph of ![]() starting with the graph of
starting with the graph of ![]() one step at a time. First, we consider the graph of
one step at a time. First, we consider the graph of ![]() . A generic point on the graph of
. A generic point on the graph of ![]() looks like
looks like ![]() . Note that if
. Note that if ![]() is odd,
is odd, ![]() can be any real number whereas if
can be any real number whereas if ![]() is even
is even ![]() so
so ![]() . If we let
. If we let ![]() , then
, then ![]() and we can change (dummy) variables[4] and obtain a new representation of the point:
and we can change (dummy) variables[4] and obtain a new representation of the point: ![]() . Note that if
. Note that if ![]() is odd,
is odd, ![]() and
and ![]() vary through all real numbers; if
vary through all real numbers; if ![]() is even,
is even, ![]() and, hence,
and, hence, ![]() . As a generic point on the graph of
. As a generic point on the graph of ![]() can be represented as
can be represented as ![]() for applicable values of
for applicable values of ![]() , we see that we can obtain every point on the graph of
, we see that we can obtain every point on the graph of ![]() by adding
by adding ![]() to each
to each ![]() -coordinate of the graph of
-coordinate of the graph of ![]() , establishing step 1 of the theorem.
, establishing step 1 of the theorem.
Proceeding to (the new!) step 2, a point on the graph of ![]() has the form
has the form ![]() . If
. If ![]() is odd, as usual,
is odd, as usual, ![]() can vary through all real numbers. If
can vary through all real numbers. If ![]() is even, we require
is even, we require ![]() or
or ![]() . If
. If ![]() , this gives
, this gives ![]() . If, on the other hand,
. If, on the other hand, ![]() , then we have
, then we have ![]() . Let
. Let ![]() and thus by assuming
and thus by assuming ![]() , we have
, we have ![]() . Once again, we change dummy variables from
. Once again, we change dummy variables from ![]() to
to ![]() and describe a generic point on the graph of
and describe a generic point on the graph of ![]() as
as ![]() . If
. If ![]() is odd,
is odd, ![]() and
and ![]() can vary through all real numbers. If
can vary through all real numbers. If ![]() is even and
is even and ![]() , then
, then ![]() and, hence,
and, hence, ![]() ; if
; if ![]() , then
, then ![]() also gives
also gives ![]() . A generic point on the graph of
. A generic point on the graph of ![]() can be represented as
can be represented as ![]() for applicable values of
for applicable values of ![]() , so we see we can obtain every point on the graph of
, so we see we can obtain every point on the graph of ![]() by dividing every
by dividing every ![]() -coordinate on the graph of
-coordinate on the graph of ![]() by
by ![]() , as per step 2 of the theorem.
, as per step 2 of the theorem.
The proof of steps 3 and 4 of Theorem 4.1} are identical to the proof of Theorem 2.2 (just with ![]() instead of
instead of ![]() ) so we invite the reader to work through the details on their own.
) so we invite the reader to work through the details on their own. ![]()
We demonstrate Theorem 4.1 in the following example.
Example 4.1.1
Example 4.1.1.1
Use Theorem 4.1 to graph the following. Label at least three points and the asymptotes. State the domain and range using interval notation.
![]()
Solution:
Graph ![]() .
.
We begin by rewriting the expression for ![]() in the form prescribed Theorem 4.1:
in the form prescribed Theorem 4.1:
![]() . We identify
. We identify ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
Step 1: add ![]() to each of the
to each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() :
:

As ![]() , we can proceed to Step 3 (dividing a real number by
, we can proceed to Step 3 (dividing a real number by ![]() results in the same real number.)
results in the same real number.)
Step 3: multiply each of the ![]() -coordinates of each point on the graph of
-coordinates of each point on the graph of ![]() by
by ![]() :
:

Step 4: add ![]() to
to ![]() -coordinates of each point on the graph of
-coordinates of each point on the graph of ![]() :
:
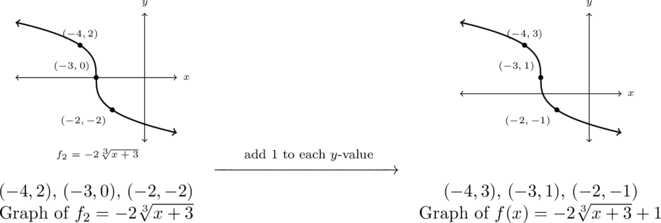
We get the domain and range of ![]() are both
are both ![]() .
.
Example 4.1.1.2
Use Theorem 4.1 to graph the following. Label at least three points and the asymptotes. State the domain and range using interval notation.
![]()
Solution:
Graph ![]() .
.
For ![]() , we identify
, we identify ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
We are asked to label three points on the graph, so we track ![]() along with
along with ![]() and
and ![]() .[5]
.[5]
Step 1: add ![]() to each of the
to each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() :
:

Step 2: divide each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() by
by ![]() :
:

Step 3: multiply each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() by
by ![]() :
:

We get the domain is ![]() and the range is
and the range is ![]() .
.
4.1.2 Other Functions involving Radicals
Now that we have some practice with basic root functions, we turn our attention to more general functions involving radicals. In general, Calculus is the best tool with which to study these functions. Nevertheless, we will use what algebra we know in combination with a graphing utility to help us visualize these functions and preview concepts which are studied in greater depth in later courses. In the table below, we summarize some of the properties of radicals from elsewhere in this text we will be using in the coming examples.
Example 4.1.2
Example 4.1.2.1
For the following function: ![]()
- Analytically:
- State the domain
- Identify the axis intercepts
- Analyze the end behavior
- Construct a sign diagram for each function using the intercepts and sketch a graph
- Using technology determine:
- The range
- The local extrema, if they exist
- Intervals where the function is increasing
- Intervals where the function is decreasing
Solution:
Analyze and graph ![]() .
.
When looking for the domain, we have two thing to watch out for: denominators (which we must make sure aren’t ![]() ) and even indexed radicals (whose radicands we must ensure are nonnegative.)
) and even indexed radicals (whose radicands we must ensure are nonnegative.)
Looking at the expression for ![]() , we have no denominators nor do we have an even indexed radical, so we are confident the domain is all real numbers,
, we have no denominators nor do we have an even indexed radical, so we are confident the domain is all real numbers, ![]() .
.
As ![]() is also on the
is also on the ![]() -axis and functions can have at most one
-axis and functions can have at most one ![]() -intercept, we know
-intercept, we know ![]() is the only
is the only ![]() -intercept.[9] That being said, we can quickly verify
-intercept.[9] That being said, we can quickly verify ![]() .
.
To determine the end behavior, we consider ![]() as
as ![]() . Using `number sense,’ [10] we have
. Using `number sense,’ [10] we have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &=& 3x \sqrt[3]{2-x} \\ &=& 3x \sqrt[3]{-x+2} \\ &\approx& (\text{big } (+)) \sqrt[3]{\text{big } (-)} \\ &=& (\text{big } (+))(\text{big } (-)) \\ &=& \text{big } (-) \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-74be46d7498a894e3617a1240bd7d8c3_l3.png)
so ![]() .
.
As ![]() we get
we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &=& 3x \sqrt[3]{-x+2} \\ &\approx & (\text{big } (-)) \sqrt[3]{\text{big } (+)} \\ &=& (\text{big } (-))(\text{big } (+)) \\ &=& \text{big } (-) \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-191b604fd6a5b0e03943b342314f0938_l3.png)
so ![]() here, too.
here, too.
To create a sign diagram for ![]() , we note that the function has zeros
, we note that the function has zeros ![]() and
and ![]()
For ![]() ,
, ![]() or
or ![]() , for
, for ![]() ,
, ![]() or
or ![]() , and for
, and for ![]() ,
, ![]() or
or ![]()
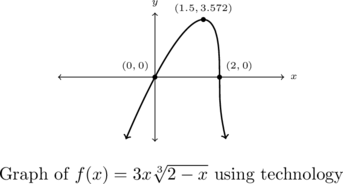
The sign diagram for ![]() is on the left. The graph of
is on the left. The graph of ![]() is on the right.
is on the right.
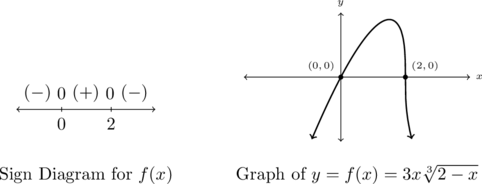
From the graph and our use of technology, the range is approximately ![]() with a local maximum (which also happens to be the maximum) at
with a local maximum (which also happens to be the maximum) at ![]() . We also see
. We also see ![]() appears to be increasing on
appears to be increasing on ![]() and decreasing on
and decreasing on ![]() .
.
It is also worth noting that there appears to be `unusual steepness’ near the ![]() -intercept
-intercept ![]() . We invite the reader to zoom in on the graph near
. We invite the reader to zoom in on the graph near ![]() to see that the function appears `locally vertical.’[11]
to see that the function appears `locally vertical.’[11]
Example 4.1.2.2
For the following function: ![]()
- Analytically:
- State the domain
- Identify the axis intercepts
- Analyze the end behavior
- Construct a sign diagram for each function using the intercepts and sketch a graph
- Using technology determine:
- The range
- The local extrema, if they exist
- Intervals where the function is increasing
- Intervals where the function is decreasing
Solution:
Analyze and graph ![]() .
.
The index of the radical in the expression for ![]() is odd, so our only concern is the denominator. Setting
is odd, so our only concern is the denominator. Setting ![]() gives
gives ![]() , which we exclude, so our domain is
, which we exclude, so our domain is ![]() or using interval notation,
or using interval notation, ![]() .
.
If we take the time to analyze the behavior of ![]() near
near ![]() , we find that as
, we find that as ![]()
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& \sqrt[3]{\frac{8t}{t+1}} \\[8pt] &\approx & \sqrt[3]{\frac{-8}{\text{small } (-)}} \\[8pt] &\approx & \sqrt[3]{\text{ big } (+)} \\[8pt] &=& \text{big } (+) \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fa1be66925e19d8467c30b0259dc7019_l3.png)
That is, as ![]() ,
, ![]() .
.
Likewise, as ![]()
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) & \approx & \sqrt[3]{\frac{-8}{\text{small } (+)}} \\[8pt] & \approx & \sqrt[3]{\text{ big } (-)} \\[8pt] &=& \text{big } (-) \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f9ef4011d1201fd91d3d8146a99e4501_l3.png)
This suggests as ![]() ,
, ![]() . This behavior points to a vertical asymptote,
. This behavior points to a vertical asymptote, ![]()
To find the ![]() -intercepts of the graph of
-intercepts of the graph of ![]() , we find the zeros of
, we find the zeros of ![]() by setting
by setting ![]() . Cubing both sides and clearing denominators gives
. Cubing both sides and clearing denominators gives ![]() or
or ![]() . Hence our
. Hence our ![]() -, and in this case,
-, and in this case, ![]() – intercept is
– intercept is ![]()
To determine the end behavior, we note that as ![]()
![]()
Hence, it stands to reason that as ![]()
![]()
This suggests the graph of ![]() has a horizontal asymptote at
has a horizontal asymptote at ![]()
To create a sign diagram for ![]() , we note that the function is undefined when
, we note that the function is undefined when ![]() (so we place a dashed line above it) and has a zero
(so we place a dashed line above it) and has a zero ![]()
When ![]() ,
, ![]() or
or ![]() , for
, for ![]() ,
, ![]() or
or ![]() , and for
, and for ![]() ,
, ![]() or
or ![]()
On the left is a sign diagram for ![]() . The graph of
. The graph of ![]() is on the right.
is on the right.
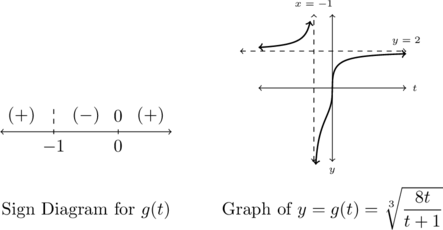
The graph confirms our suspicions about the asymptotes ![]() and
and ![]()
Moreover, the range appears to be ![]() .
.
We could check if the graph ever crosses its horizontal asymptote by attempting to solve ![]() . Cubing both sides and clearing denominators gives
. Cubing both sides and clearing denominators gives ![]() which results in
which results in ![]() , a contradiction. This proves
, a contradiction. This proves ![]() is not in the range, as we had suspected.
is not in the range, as we had suspected.
Scanning the graph, there appears to be no local extrema, and, moreover, the graph suggests ![]() is increasing on
is increasing on ![]() and again on
and again on ![]() . As with the previous example, the graph appears locally vertical near its intercept
. As with the previous example, the graph appears locally vertical near its intercept ![]() .
.
Example 4.1.2.3
For the following function: ![]()
- Analytically:
- State the domain
- Identify the axis intercepts
- Analyze the end behavior
- Construct a sign diagram for each function using the intercepts and sketch a graph
- Using technology determine:
- The range
- The local extrema, if they exist
- Intervals where the function is increasing
- Intervals where the function is decreasing
Solution:
Analyze and graph ![]() .
.
The expression for ![]() has both a denominator and an even-indexed radical, so we have to be extra cautious here.
has both a denominator and an even-indexed radical, so we have to be extra cautious here.
Fortunately for us, the quantity ![]() for al real numbers
for al real numbers ![]() . Not only does this mean
. Not only does this mean ![]() is always defined, it also tells us
is always defined, it also tells us ![]() for all
for all ![]() , too. This means the domain of
, too. This means the domain of ![]() is all real numbers,
is all real numbers, ![]()
Solving for the zeros of ![]() gives only
gives only ![]() , and we find, once again,
, and we find, once again, ![]() is both our lone
is both our lone ![]() – and
– and ![]() -intercept.
-intercept.
Moving on to end behavior, as ![]() , the term
, the term ![]() is the dominant term in the radicand in the denominator. As such,
is the dominant term in the radicand in the denominator. As such,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(x) &=& \frac{3x}{\sqrt{x^2 + 1}} \\[8pt] & \approx & \frac{3x}{\sqrt{x^2}} \\[8pt] &=& \frac{3x}{|x|} \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fd61310d640b972b4c2e0d454bca15bc_l3.png)
As ![]() ,
, ![]() (because
(because ![]() ), so
), so
![]()
so ![]() .
.
Likewise, as ![]() ,
, ![]() (because
(because ![]() ) and hence,
) and hence,
![]()
so ![]() .
.
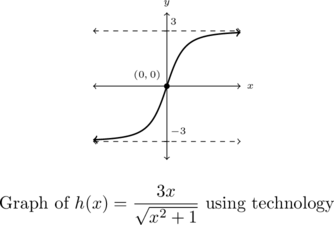
This analysis suggests the graph of ![]() has not one, but two horizontal asymptotes.[12] The graph of
has not one, but two horizontal asymptotes.[12] The graph of ![]() below on the right bears this out.
below on the right bears this out.
The domain of ![]() is all real number and the only zero of
is all real number and the only zero of ![]() is
is ![]() , so the sign diagram for
, so the sign diagram for ![]() is fairly straight forward. For
is fairly straight forward. For ![]() ,
, ![]() or
or ![]() and for
and for ![]() ,
, ![]() or
or ![]()
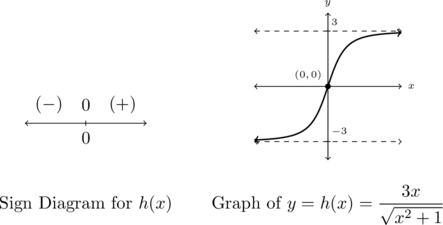
From the graph, we see the range of ![]() appears to be
appears to be ![]()
Attempting to solve ![]() gives, in either case,
gives, in either case, ![]() which reduces to
which reduces to ![]() , a contradiction. Hence, the graph of
, a contradiction. Hence, the graph of ![]() never reaches its horizontal asymptotes.
never reaches its horizontal asymptotes.
Moreover, ![]() appears to be always increasing, with no local extrema or `unusual’ steepness.
appears to be always increasing, with no local extrema or `unusual’ steepness.
One last remark: it appears as if the graph of ![]() is symmetric about the origin. We check
is symmetric about the origin. We check ![]() which verifies
which verifies ![]() is odd.
is odd.
Example 4.1.2.4
For the following function: ![]()
- Analytically:
- State the domain
- Identify the axis intercepts
- Analyze the end behavior
- Construct a sign diagram for each function using the intercepts and sketch a graph
- Using technology determine:
- The range
- The local extrema, if they exist
- Intervals where the function is increasing
- Intervals where the function is decreasing
Solution:
Analyze and graph ![]() .
.
The first thing to note about the expression ![]() is that
is that ![]() .
.
Hence, we must exclude ![]() from the domain straight away.
from the domain straight away.
Next, we have an even-indexed radical expression: ![]() . In order for this to return a real number, we require
. In order for this to return a real number, we require ![]() . Instead of using a sign diagram to solve this, we opt instead to carefully use properties of radicals. Isolating
. Instead of using a sign diagram to solve this, we opt instead to carefully use properties of radicals. Isolating ![]() , we have
, we have ![]() . As the root functions are increasing, we can apply the fourth root to both sides and preserve the inequality:
. As the root functions are increasing, we can apply the fourth root to both sides and preserve the inequality: ![]() which gives[13]
which gives[13] ![]() . Note that
. Note that ![]() does not satisfy this inequality, thus restricting
does not satisfy this inequality, thus restricting ![]() in this manner takes care of both domain issues, so the domain is
in this manner takes care of both domain issues, so the domain is ![]() .
.
Next, we look for zeros. Setting ![]() gives
gives ![]() . After squaring both sides, we get
. After squaring both sides, we get ![]() or
or ![]() . Extracting fourth roots, we get
. Extracting fourth roots, we get ![]() . Both of these are (barely!) in the domain of
. Both of these are (barely!) in the domain of ![]() , so our
, so our ![]() intercepts are
intercepts are ![]() and
and ![]()
Note, the graph of ![]() has no
has no ![]() -intercept, because
-intercept, because ![]() is undefined (
is undefined (![]() is not in the domain of
is not in the domain of ![]() ).
).
Concerning end behavior, we note the term ![]() dominates the radicand
dominates the radicand ![]() as
as ![]() , hence,
, hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} r(t) &=& \frac{\sqrt{16t^4-1}}{t} \\[8pt] &\approx & \frac{\sqrt{16t^4}}{t} \\[8pt] &=& \frac{4t^2}{t} \\[8pt] &=& 4t \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-56537a0a018555b4534b355f2f5f618b_l3.png)
This suggests the graph of ![]() has a slant asymptote with slope
has a slant asymptote with slope ![]() .[14]
.[14]
To construct the sign diagram for ![]() we note
we note ![]() has two zeros,
has two zeros, ![]() .
.
For ![]() ,
, ![]() or
or ![]() and when
and when ![]() ,
, ![]() or
or ![]() . When
. When ![]() ,
, ![]() is undefined so we have removed that segment from the diagram, as seen below on the left. The graph of
is undefined so we have removed that segment from the diagram, as seen below on the left. The graph of ![]() is on the right.
is on the right.
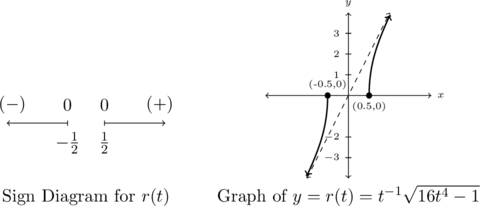
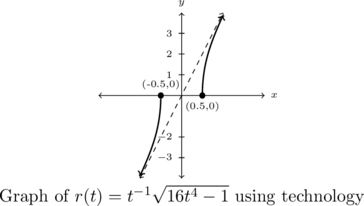
We see the range appears to be all real numbers, ![]() .
.
It appears as if ![]() is increasing on
is increasing on ![]() and again on
and again on ![]() .
.
The graph does appear to be asymptotic to ![]() , and it also appears to be symmetric about the origin. Sure enough, we find
, and it also appears to be symmetric about the origin. Sure enough, we find ![]() , proving
, proving ![]() is an odd function.
is an odd function.
We end this section with a classic application of root functions.
Example 4.1.3
Example 4.1.3.1
Carl wishes to get high speed internet service installed in his remote Sasquatch observation post located ![]() miles from Route
miles from Route ![]() . The nearest junction box is located
. The nearest junction box is located ![]() miles down the road from the post, as indicated in the diagram below. Suppose it costs
miles down the road from the post, as indicated in the diagram below. Suppose it costs ![]() per mile to run cable along the road and
per mile to run cable along the road and ![]() per mile to run cable off of the road.
per mile to run cable off of the road.
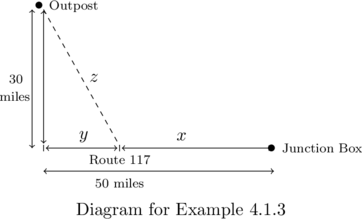
Write an expression, ![]() , which computes the cost of connecting the Junction Box to the Outpost as a function of
, which computes the cost of connecting the Junction Box to the Outpost as a function of ![]() , the number of miles the cable is run along Route
, the number of miles the cable is run along Route ![]() before heading off road directly towards the Outpost. Determine a reasonable applied domain for the problem.
before heading off road directly towards the Outpost. Determine a reasonable applied domain for the problem.
Solution:
Write an expression ![]() .
.
The cost is broken into two parts: the cost to run cable along Route ![]() at
at ![]() per mile, and the cost to run it off road at
per mile, and the cost to run it off road at ![]() per mile.
per mile.
![]() represents the miles of cable run along Route
represents the miles of cable run along Route ![]() , thus the cost for that portion is
, thus the cost for that portion is ![]() .
.
From the diagram, we see that the number of miles the cable is run off road is ![]() , so the cost of that portion is
, so the cost of that portion is ![]() .
.
Hence, the total cost is ![]() .
.
Our next goal is to determine ![]() in terms of
in terms of ![]() . The diagram suggests we can use the Pythagorean Theorem to get
. The diagram suggests we can use the Pythagorean Theorem to get ![]() .
.
But we also see ![]() so that
so that ![]() .
.
Substituting ![]() in for
in for ![]() we obtain
we obtain ![]() .
.
Solving for ![]() , we obtain
, we obtain ![]() .
.
Because ![]() represents a distance, we choose
represents a distance, we choose ![]() .
.
Hence, the cost as a function of ![]() is given by
is given by ![]() . From the context of the problem, we have
. From the context of the problem, we have ![]() .
.
Example 4.1.3.1
Carl wishes to get high speed internet service installed in his remote Sasquatch observation post located ![]() miles from Route
miles from Route ![]() . The nearest junction box is located
. The nearest junction box is located ![]() miles down the road from the post, as indicated in the diagram below. Suppose it costs
miles down the road from the post, as indicated in the diagram below. Suppose it costs ![]() per mile to run cable along the road and
per mile to run cable along the road and ![]() per mile to run cable off of the road.
per mile to run cable off of the road.

Graph ![]() on its domain. What is the minimum cost? How far along Route
on its domain. What is the minimum cost? How far along Route ![]() should the cable be run before turning off of the road?
should the cable be run before turning off of the road?
Solution:
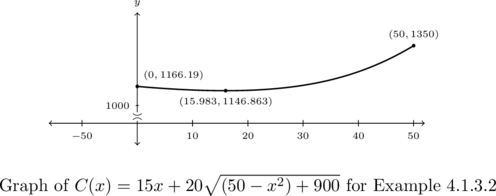
Graph ![]() .
.
We graph ![]() below and find our (local) minimum to be at the point
below and find our (local) minimum to be at the point ![]() , using technology.
, using technology.
Here the ![]() -coordinate tells us that in order to minimize cost, we should run
-coordinate tells us that in order to minimize cost, we should run ![]() miles of cable along Route 117 and then turn off of the road and head towards the outpost. The
miles of cable along Route 117 and then turn off of the road and head towards the outpost. The ![]() -coordinate tells us that the minimum cost, in dollars, to do so is 1146.86 dollars. The ability to stream live SasquatchCasts? Priceless.
-coordinate tells us that the minimum cost, in dollars, to do so is 1146.86 dollars. The ability to stream live SasquatchCasts? Priceless.
4.1.3 Section Exercises
In Exercises 1 – 8, given the pair of functions ![]() and
and ![]() , sketch the graph of
, sketch the graph of ![]() by starting with the graph of
by starting with the graph of ![]() and using Theorem 4.1. Track at least two points and state the domain and range using interval notation.
and using Theorem 4.1. Track at least two points and state the domain and range using interval notation.
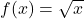 and
and 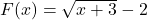
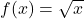 and
and 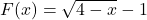
![Rendered by QuickLaTeX.com f(x) = \sqrt[3]{x}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9b50ca065c07a421d5aaef1e13245aae_l3.png) and
and ![Rendered by QuickLaTeX.com F(x) = \sqrt[3]{x-1}-2](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4d42e14b2457dbdbc124fd5578172fc2_l3.png)
![Rendered by QuickLaTeX.com f(x) = \sqrt[3]{x}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9b50ca065c07a421d5aaef1e13245aae_l3.png) and
and ![Rendered by QuickLaTeX.com F(x) = -\sqrt[3]{8x + 8} + 4](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c9efa3e18a11af21e6ce2d4d74bde45f_l3.png)
![Rendered by QuickLaTeX.com f(x) = \sqrt[4]{x}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-887452a0fb9f7210a8e1a969d4ee2df1_l3.png) and
and ![Rendered by QuickLaTeX.com F(x) = \sqrt[4]{x-1}-2](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-42c9079f6a3933b1e3314abbf1ff04e8_l3.png)
![Rendered by QuickLaTeX.com f(x) = \sqrt[4]{x}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-887452a0fb9f7210a8e1a969d4ee2df1_l3.png) and
and ![Rendered by QuickLaTeX.com F(x) = -3\sqrt[4]{x - 7} +1](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-151629967bddbaffaa5377596fe5bbe8_l3.png)
![Rendered by QuickLaTeX.com f(x) = \sqrt[5]{x}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-371ba74227f12831d7a1bde147e863d0_l3.png) and
and ![Rendered by QuickLaTeX.com F(x) = \sqrt[5]{x + 2} + 3](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9e7db4008eb160096aabd7f2b29e150b_l3.png)
![Rendered by QuickLaTeX.com f(x) = \sqrt[8]{x}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b4652d4be50de97a2a58add38a35c3c2_l3.png) and
and ![Rendered by QuickLaTeX.com F(x) = \sqrt[8]{-x} - 2](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-470238f477e1d2e13e408873a753dd5e_l3.png)
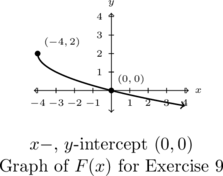
In Exercises 9 – 10, find a formula for each function below in the form ![]() .
.
NOTE: There may be more than one solution!
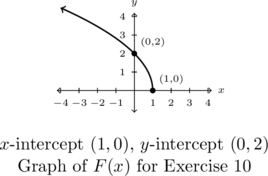
In Exercises 11 – 12, find a formula for each function below in the form ![]() .
.
NOTE: There may be more than one solution!
-
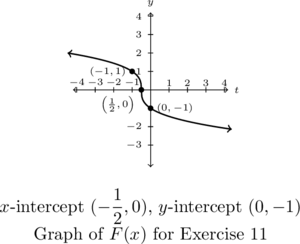
-
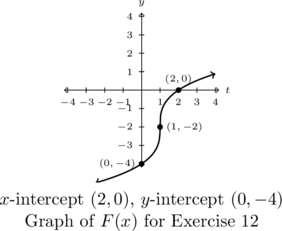
- Use the fact that the
 th root functions are increasing to solve the following polynomial inequalities:
th root functions are increasing to solve the following polynomial inequalities:
For the following inequalities, remember
![Rendered by QuickLaTeX.com \sqrt[n]{x^{n}} = |x|](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5ccf1dbb879e81dd8b2ba41bf425557f_l3.png) if
if 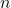 is even:
is even:
For each function in Exercises 14 – 21 below
- Analytically:
- State the domain
- Determine the axis intercepts
- Analyze the end behavior
- Construct a sign diagram for each function using the intercepts and sketch a graph.
- Using technology determine:
- The range
- The local extrema, if they exist
- Intervals where the function is increasing/decreasing
- Any `unusual steepness’ or `local’ verticality
- Vertical asymptotes
- Horizontal/slant asymptotes
- Comment on any observed symmetry
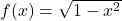
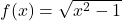

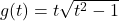
![Rendered by QuickLaTeX.com f(x) = \sqrt[4]{\dfrac{16x}{x^{2} - 9}}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6def95b38ad724dc7e237a82e9575165_l3.png)
![Rendered by QuickLaTeX.com f(x) = \dfrac{5x}{\sqrt[3]{x^{3} + 8}}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-17058ab84d35a1ef1e8007d0e2d83b00_l3.png)
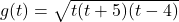
![Rendered by QuickLaTeX.com g(t) = \sqrt[3]{t^{3} + 3t^{2} - 6t - 8}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-949a64f9d72def308aa86c6af9a6163e_l3.png)
- Rework Example 4.1.3 so that the outpost is 10 miles from Route 117 and the nearest junction box is 30 miles down the road for the post.
- The volume
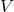 of a right cylindrical cone depends on the radius of its base
of a right cylindrical cone depends on the radius of its base  and its height
and its height 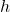 and is given by the formula
and is given by the formula 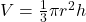 . The surface area
. The surface area 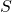 of a right cylindrical cone also depends on
of a right cylindrical cone also depends on  and
and 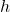 according to the formula
according to the formula 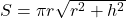 . In the following problems, suppose a cone is to have a volume of 100 cubic centimeters.
. In the following problems, suppose a cone is to have a volume of 100 cubic centimeters.
- Use the formula for volume to find the height as a function of
 ,
, 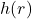 .
. - Use the formula for surface area along with your answer to 23a to find the surface area as a function of
 ,
, 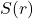 .
. - Use your calculator to find the values of
 and
and 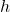 which minimize the surface area. What is the minimum surface area? Round your answers to two decimal places.
which minimize the surface area. What is the minimum surface area? Round your answers to two decimal places.
- Use the formula for volume to find the height as a function of
- The period of a pendulum in seconds is given by
![Rendered by QuickLaTeX.com \[T = 2\pi \sqrt{\dfrac{L}{g}}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9fecd62ee64789f6d4d2b44a20c27413_l3.png)
(for small displacements) where
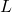 is the length of the pendulum in meters and
is the length of the pendulum in meters and 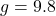 meters per second per second is the acceleration due to gravity. My Seth-Thomas antique schoolhouse clock needs
meters per second per second is the acceleration due to gravity. My Seth-Thomas antique schoolhouse clock needs 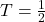 second and I can adjust the length of the pendulum via a small dial on the bottom of the bob. At what length should I set the pendulum?
second and I can adjust the length of the pendulum via a small dial on the bottom of the bob. At what length should I set the pendulum? - According to Einstein’s Theory of Special Relativity, the observed mass of an object is a function of how fast the object is traveling. Specifically, if
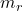 is the mass of the object at rest,
is the mass of the object at rest,  is the speed of the object and
is the speed of the object and  is the speed of light, then the observed mass of the object
is the speed of light, then the observed mass of the object 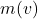 is given by:
is given by:
![Rendered by QuickLaTeX.com \[m(v) = \dfrac{m_{r}}{\sqrt{1 - \dfrac{v^{2}}{c^{2}}}}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d76c89dcf820bc0796e73f0fbf8e6575_l3.png)
- State the applied domain of the function.
- Compute
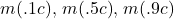 and
and 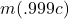 .
. - As
 , what happens to
, what happens to 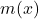 ?
? - How slowly must the object be traveling so that the observed mass is no greater than 100 times its mass at rest?
- Find the inverse of
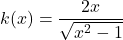 .
.
Section 4.1 Exercise Answers can be found in the Appendix … Coming soon
- Although we discussed imaginary numbers in Section 1.5, we restrict our attention to real numbers in this section. ↵
- See Exercise 13. ↵
- Because, otherwise,
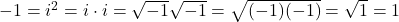 , a contradiction. ↵
, a contradiction. ↵ - again this is because every real number can be represented as both
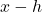 for some value
for some value 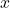 and as
and as 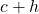 for some value
for some value  . ↵
. ↵ - As
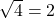 , we know
, we know 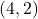 is on the graph of
is on the graph of 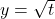 . ↵
. ↵ - i.e., if
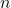 is odd,
is odd, 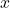 ,
,  , and
, and 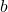 can be any real numbers; if, on the other hand
can be any real numbers; if, on the other hand 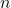 is even,
is even, 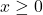 ,
, 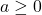 , and
, and 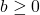 . ↵
. ↵ - a.k.a., `Inverse Properties.' See Section 5.1. ↵
- i.e., root functions are increasing. ↵
- Why is this, again? ↵
- remember this means we use the adjective `big' here to mean large in absolute value ↵
- Of course, the Vertical Line Test prohibits the graph from actually being a vertical line. This behavior is more precisely defined and more closely studied in Calculus. ↵
- We warned you this was coming
 see the discussion following Theorem 3.3 in Section 3.2. ↵
see the discussion following Theorem 3.3 in Section 3.2. ↵ - Recall:
![Rendered by QuickLaTeX.com \sqrt[n]{x^n} = |x|](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5c9bf00f6faf055a9464d7fd13357ee5_l3.png) , not
, not 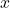 , if
, if 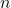 is even. ↵
is even. ↵ - Note: this analysis suggests the slant asymptote is
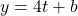 , but from this analysis, we cannot determine the value of
, but from this analysis, we cannot determine the value of 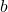 . As with slant asymptotes in Section 3.2, we'd need to perform a more detailed analysis which we omit in this case owing to the complexity of the function. ↵
. As with slant asymptotes in Section 3.2, we'd need to perform a more detailed analysis which we omit in this case owing to the complexity of the function. ↵

![Rendered by QuickLaTeX.com \begin{array}{rcl} F(x) = (2x-1)^2 + 1 &=& \left[2 \left(x - \frac{1}{2}\right)\right]^2+1 \\ &=& (2)^2 \left(x - \frac{1}{2}\right)^2 + 1 \\ &=& 4\left(x - \frac{1}{2}\right)^2 + 1 \end{array}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6108352598ee757860c77be02aad6a06_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{rcl} F(x) = \frac{2}{(1-x)^3}- 5 &=& \frac{2}{[(-1)(x-1)]^3} - 5 \\ &=& \frac{2}{(-1)^3(x-1)^3} - 5\\ &=& \frac{2}{- (x-1)^3} - 5 \\ &=& \frac{-2}{(x-1)^3} - 5 \end{array}](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1edc62b08c14fa2a7797e26108ed507e_l3.png)