5.6 Solving Equations Involving Logarithmic Functions
In Section 5.5 we solved equations and inequalities involving exponential functions using one of two basic strategies. We now turn our attention to equations and inequalities involving logarithmic functions, and not surprisingly, there are two basic strategies to choose from.
For example, per Theorem 5.7, the only solution to ![]() is
is ![]() . Now consider
. Now consider ![]() . To use Theorem 5.7, we need to rewrite
. To use Theorem 5.7, we need to rewrite ![]() as a logarithm base
as a logarithm base ![]() . Theorem 5.6 gives us
. Theorem 5.6 gives us ![]() . Hence,
. Hence, ![]() is equivalent to
is equivalent to ![]() so that
so that ![]() .
.
A second approach to solving ![]() us to apply the corresponding exponential function,
us to apply the corresponding exponential function, ![]() to both sides:
to both sides: ![]() so
so ![]() .
.
A third approach to solving ![]() is to use Theorem 5.6 to rewrite
is to use Theorem 5.6 to rewrite ![]() as
as ![]() , so
, so ![]() .
.
In the grand scheme of things, all three approaches we have presented to solve ![]() are mathematically equivalent, so we opt to choose the last approach in our summary below.
are mathematically equivalent, so we opt to choose the last approach in our summary below.
Steps for Solving an Equation Involving Logarithmic Functions
- Isolate the logarithmic function.
- (a) If convenient, express both sides as logs with the same base and equate
arguments.
(b) Otherwise, rewrite the log equation as an exponential equation.
Example 5.6.1
Example 5.6.1.1
Solve the following equations. Check your solutions graphically.
![]()
Solution:
Solve ![]() for
for ![]() .
.
We have the same base on both sides of the equation ![]() , thus we equate the arguments (what’s inside) of the logs to get
, thus we equate the arguments (what’s inside) of the logs to get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} 1-3x & = & x^2-3 \\ x^2+3x-4 & = & 0 \\ x=-4 & \text{ and } & x=1 \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-28d9ee3f944380d4c91d0738f40f32df_l3.png)
To check these answers using a graph, we make use of the change of base formula and graph ![]() and
and ![]() . We see these graphs intersect only at
. We see these graphs intersect only at ![]() . however.
. however.
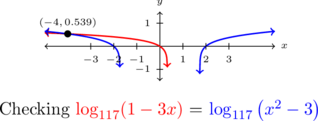
To see what happened to the solution ![]() , we substitute it into our original equation to obtain
, we substitute it into our original equation to obtain ![]() . While these expressions look identical, neither is a real number,[1] which means
. While these expressions look identical, neither is a real number,[1] which means ![]() is not in the domain of the original equation, and is not a solution.
is not in the domain of the original equation, and is not a solution.
Example 5.6.1.2
Solve the following equations. Check your solutions graphically.
![]()
Solution:
Solve ![]() for
for ![]() .
.
To solve ![]() , we first isolate the logarithm and get
, we first isolate the logarithm and get ![]() . Rewriting
. Rewriting ![]() as an exponential equation, we get is
as an exponential equation, we get is ![]() , so
, so ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 2 - \ln(t-3) & = & 1 & \text{Isolate the logarithm} \\ \ln(t-3) & = & 1 & \\[4pt] e^{1} & = & t-3 & \text{Rewrite as an exponential} \\ t & = & e+3 & \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a7c5dce9dd8435caaa14adc641aeb766_l3.png)
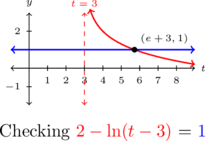
A graph shows the graphs of ![]() and
and ![]() intersect at
intersect at ![]() .
.
Example 5.6.1.3
Solve the following equations. Check your solutions graphically.
![]()
Solution:
Solve ![]() for
for ![]() .
.
We start solving ![]() by using the Product Rule for logarithms to rewrite the equation
by using the Product Rule for logarithms to rewrite the equation
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \log_{6}\left[(x+4)(3-x)\right] &= & 1 & \text{Rewrite as an exponential} \\ 6^{1} & = & (x+4)(3-x) & \\ x^2+x-6 &=& 0 & \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-88442f709414f90847424fed5a1cc1fb_l3.png)
We get two solutions: ![]() and
and ![]() .
.
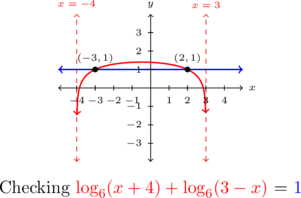
Using the change of base formula, we graph ![]() and
and ![]() and we see the graphs intersect twice, at
and we see the graphs intersect twice, at ![]() and
and ![]() , as required.
, as required.
Example 5.6.1.4
Solve the following equations. Check your solutions graphically.
![]()
Solution:
Solve ![]() for
for ![]() .
.
Taking a cue from the previous problem, we begin solving ![]() by first collecting the logarithms on the same side,
by first collecting the logarithms on the same side,
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \log_{7}(1-2t) + \log_{7}(3-t) & = & 1 & \text{Power Rule} \\ \log_{7}[(1-2t)(3-t)] & = & 1 & \text{Rewrite as an exponential} \\[2pt] 7^{1} & =& (1-2t)(3-t) & \\ 7 & = & 2t^2 - 7t + 3 & \\ 2t^2-7t-4 &= &0 & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-442495b810931bfc256351bdeefed5d5_l3.png)
Solving, we find ![]() and
and ![]() .
.
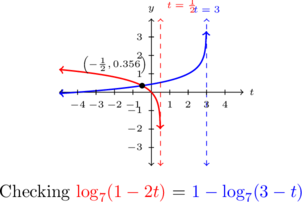
Once again, we use the change of base formula and find the graphs of ![]() and
and ![]() intersect only at
intersect only at ![]() .
.
Checking ![]() in the original equation produces
in the original equation produces ![]() , showing
, showing ![]() is not in the domain of
is not in the domain of ![]() nor
nor ![]() .
.
Example 5.6.1.5
Solve the following equations. Check your solutions graphically.
![]()
Solution:
Solve ![]() for
for ![]() .
.
Our first step in solving ![]() is to gather the logarithms to one side of the equation:
is to gather the logarithms to one side of the equation:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \log_{2}(x+3) - \log_{2}(6-x) & = & 3 & \\ \log_{2}\left(\frac{x+3}{6-x}\right) & = & 3 & \text{Quotient Rule} \\[2pt] 2^{3} & = & \frac{x+3}{6-x} & \text{Rewrite as an exponential} \\ 8(6-x) & = & x+3 & \\ x & = & 5 & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-12947a5559f4e5adbcd1d6ec8f813515_l3.png)
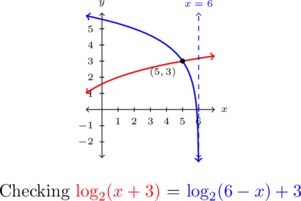
Using the change of base once again, we graph ![]() and
and ![]() and find they intersect at
and find they intersect at ![]() .
.
Example 5.6.1.6
Solve the following equations. Check your solutions graphically.
![]()
Solution:
Solve ![]() for
for ![]() .
.
Our first step in solving ![]() is to gather the logs on one side of the equation. We obtain
is to gather the logs on one side of the equation. We obtain ![]() but find we need a common base to combine the logs.
but find we need a common base to combine the logs.
As ![]() is a power of
is a power of ![]() , we use change of base to convert
, we use change of base to convert ![]() . Hence, our original equation becomes
. Hence, our original equation becomes
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 1 & = & 2 \log_{2}(t) - 2 \left(\frac{1}{2} \log_{2}(t+1)\right) & \\ [2pt] 1 &= & 2\log_{2}(t) - \log_{2}(t+1) & \\ [2pt] 1 & = & \log_{2}\left(t^2\right) - \log_{2}(t+1) & \text{Power Rule} \\ [6pt] 1 & = & \log_{2}\left( \dfrac{t^{2}}{t+1}\right) & \text{Quotient Rule} \\ \frac{t^{2}}{t+1} & = & 2 & \text{Rewrite as a exponential} \\ t^2 -2t-2 & = & 0 & \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-58bae889996c7b25df8f8e3d4e5817a7_l3.png)
Using the quadratic formula, we obtain ![]() .
.
One last time, we use the change of base formula and graph ![]() and
and ![]() . We see the graphs intersect only at
. We see the graphs intersect only at ![]() .
.
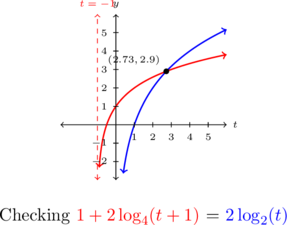
Note the solution ![]() . Hence if substituted into the original equation, the term
. Hence if substituted into the original equation, the term ![]() is undefined, which explains why the graphs intersect only once.
is undefined, which explains why the graphs intersect only once.
If nothing else, Example 5.6.1 demonstrates the importance of checking for extraneous solutions[2] when solving equations involving logarithms. Even though we checked our answers graphically, extraneous solutions are easy to spot: any supposed solution which causes the argument of a logarithm to be negative must be discarded.
While identifying extraneous solutions is important, it is equally important to understand which machinations create the opportunity for extraneous solutions to appear. In the case of Example 5.6.1, extraneous solutions, by and large, result from using the Power, Product, or Quotient Rules. We encourage the reader to take the time to track each extraneous solution found in Example 5.6.1 backwards through the solution process to see at precisely which step it fails to be a solution.
Example 5.6.2
Example 5.6.2.1
The function ![]() is one-to-one.
is one-to-one.
Write a formula for ![]() and check your answer graphically.
and check your answer graphically.
Solution:
Write a formula for ![]() and check your answer graphically.
and check your answer graphically.
We first write ![]() then interchange the
then interchange the ![]() and
and ![]() and solve for
and solve for ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} y & = & f(x) & \\ y & = & \dfrac{\log(x)}{1-\log(x)} & \\[8pt] x & = & \dfrac{\log(y)}{1-\log(y)} & \text{Interchange $x$ and $y$.}\\[8pt] x\left(1-\log(y)\right) & = & \log(y) & \\ x - x\log(y) & = & \log(y) & \\ x & = & x \log(y) + \log(y) & \\ x & = & (x+1) \log(y) & \\ \dfrac{x}{x+1} & = & \log(y) & \\ y & = & 10^{\frac{x}{x+1}} & \text{Rewrite as an exponential equation.}\\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e2d12e64afd522eabe24644631dccc9c_l3.png)
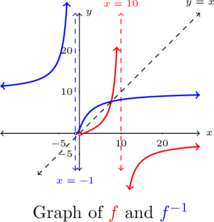
We have ![]() . Graphing
. Graphing ![]() and
and ![]() on the same graph produces the required symmetry about
on the same graph produces the required symmetry about ![]() .
.
Example 5.6.2.2
The function ![]() is one-to-one.
is one-to-one.
Solve ![]()
Solution:
Solve ![]() .
.
Recognizing ![]() as
as ![]() , we have
, we have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} x & = & f^{-1}(1) \\ & = & 10^{\frac{1}{1+1}} \\ & = & 10^{\frac{1}{2}} \\ & = & \sqrt{10} \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-56acb022a008a7263402d51efe7728c9_l3.png)
To check our answer algebraically, first recall ![]() . Next, we know
. Next, we know ![]() . Hence,
. Hence, ![]() . It follows that
. It follows that ![]() , as required.
, as required.
5.6.1 Section Exercises
In Exercises 1 – 24, solve the equation analytically.
In Exercises 25 – 30, state the domain of the function.
Section 5.6 Exercise Answers can be found in the Appendix … Coming soon

