7.3 Graphs of Sine and Cosine
In Section 7.2, we discussed how to interpret the sine and cosine of real numbers. To review, we identify a real number ![]() with an oriented angle
with an oriented angle ![]() measuring
measuring ![]() radians[1] and define
radians[1] and define ![]() and
and ![]() . Every real number can be identified with one and only one angle
. Every real number can be identified with one and only one angle ![]() this way, therefore the domains of the functions
this way, therefore the domains of the functions ![]() and
and ![]() are all real numbers,
are all real numbers, ![]() .
.
When it comes to range, recall that the sine and cosine of angles are coordinates of points on the Unit Circle and hence, each fall between ![]() and
and ![]() inclusive. As the real number line,[2] when wrapped around the Unit Circle completely covers the circle, we can be assured that every point on the Unit Circle corresponds to at least one real number. Putting these two facts together, we conclude the range of
inclusive. As the real number line,[2] when wrapped around the Unit Circle completely covers the circle, we can be assured that every point on the Unit Circle corresponds to at least one real number. Putting these two facts together, we conclude the range of ![]() and
and ![]() are both
are both ![]() . We summarize these two important facts below.
. We summarize these two important facts below.
Theorem 7.5 Domain and Range of the Cosine and Sine Functions
- The function
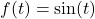
- has a domain of
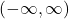
- has a range of
![Rendered by QuickLaTeX.com [-1,1]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-01968fac04e5065aa6fb740566b7905b_l3.png)
- has a domain of
- The function
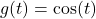
- has a domain of
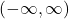
- has a range of
![Rendered by QuickLaTeX.com [-1,1]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-01968fac04e5065aa6fb740566b7905b_l3.png)
- has a domain of
Our aim in this section is to become familiar with the graphs of ![]() and
and ![]() . To that end, we begin by making a table and plotting points. We’ll start by graphing
. To that end, we begin by making a table and plotting points. We’ll start by graphing ![]() by making a table of values and plotting the corresponding points. We’ll keep the independent variable `
by making a table of values and plotting the corresponding points. We’ll keep the independent variable `![]() ‘ for now and use the default `
‘ for now and use the default `![]() ‘ as our dependent variable.[3] Note in the graph below, on the right, the scale of the horizontal and vertical axis is far from 1:1. (We will present a more accurately scaled graph shortly.)
‘ as our dependent variable.[3] Note in the graph below, on the right, the scale of the horizontal and vertical axis is far from 1:1. (We will present a more accurately scaled graph shortly.)
![Rendered by QuickLaTeX.com \[\begin{array}{ccc}\begin{array}{|r||r|r|} \hline t & \sin(t) & (t,\sin(t)) \\ \hline 0 & 0 & (0, 0) \\ [1pt] \hline \frac{\pi}{4} & \frac{\sqrt{2}}{2} & \left(\frac{\pi}{4}, \frac{\sqrt{2}}{2}\right) \\ [1pt] \hline \frac{\pi}{2} & 1 & \left(\frac{\pi}{2}, 1\right) \\ [1pt] \hline \frac{3\pi}{4} & \frac{\sqrt{2}}{2} & \left(\frac{3\pi}{4}, \frac{\sqrt{2}}{2}\right) \\ [1pt] \hline \pi & 0 & (\pi, 0) \\ [1pt] \hline \end{array} & \qquad \qquad & \begin{array}{|r||r|r|} \hline t & \sin(t) & (t,\sin(t)) \\ \hline \frac{5\pi}{4} & -\frac{\sqrt{2}}{2} & \left(\frac{5\pi}{4}, -\frac{\sqrt{2}}{2}\right) \\ [1pt] \hline \frac{3\pi}{2} & -1 & \left(\frac{3\pi}{2}, -1 \right) \\ [1pt] \hline \frac{7\pi}{4} & -\frac{\sqrt{2}}{2} & \left(\frac{7\pi}{4}, -\frac{\sqrt{2}}{2}\right) \\ [1pt] \hline 2\pi & 0 & (2\pi, 0) \\ [1pt] \hline \end{array} \\ \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e8b07345b5720a0f87124df1e8da29ae_l3.png)
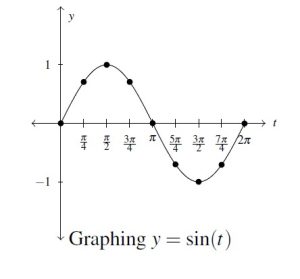
If we plot additional points, we soon find that the graph repeats itself. This shouldn’t come as too much of a surprise considering Theorem 7.3. In fact, in light of that theorem, we expect the function to repeat itself every ![]() units. Below is a more accurately scaled graph highlighting the portion we had already graphed above. The graph is often described as having a `wavelike’ nature and is sometimes called a sine wave or, more technically, a sinusoid.
units. Below is a more accurately scaled graph highlighting the portion we had already graphed above. The graph is often described as having a `wavelike’ nature and is sometimes called a sine wave or, more technically, a sinusoid.
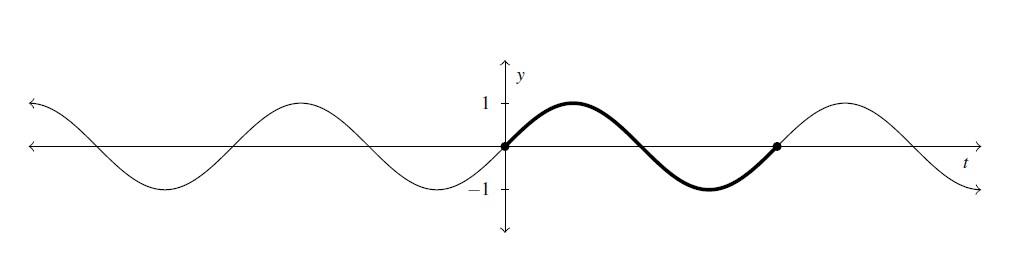
Note that by copying the highlighted portion of the graph and pasting it end-to-end, we obtain the entire graph of ![]() . We give this `repeating’ property a name.
. We give this `repeating’ property a name.
Definition 7.4 Periodic Functions
A function ![]() is said to be periodic if there is a real number
is said to be periodic if there is a real number ![]() so that
so that ![]() for all real numbers
for all real numbers ![]() in the domain of
in the domain of ![]() . The smallest positive number
. The smallest positive number ![]() for which
for which ![]() for all real numbers
for all real numbers ![]() in the domain of
in the domain of ![]() , if it exists, is called the period of
, if it exists, is called the period of ![]() .
.
We have already seen a family of periodic functions in Section 1.3.1: the constant functions. However, despite being periodic a constant function has no period. (We’ll leave that odd gem as an exercise for you.)
Returning to ![]() , we see that by Definition 7.4,
, we see that by Definition 7.4, ![]() is periodic as
is periodic as ![]() . To determine the period of
. To determine the period of ![]() , we need to find the smallest real number
, we need to find the smallest real number ![]() so that
so that ![]() for all real numbers
for all real numbers ![]() or, said differently, the smallest positive real number
or, said differently, the smallest positive real number ![]() such that
such that ![]() for all real numbers
for all real numbers ![]() .
.
We know that ![]() for all real numbers
for all real numbers ![]() but the question remains if any smaller real number will do the trick. Suppose
but the question remains if any smaller real number will do the trick. Suppose ![]() and
and ![]() for all real numbers
for all real numbers ![]() . Then, in particular,
. Then, in particular, ![]() so that
so that ![]() . From this we know
. From this we know ![]() is a multiple of
is a multiple of ![]() . Given
. Given ![]() , we know
, we know ![]() . Hence,
. Hence, ![]() so the period of
so the period of ![]() is
is ![]() .
.
Having period ![]() essentially means that we can completely understand everything about the function
essentially means that we can completely understand everything about the function ![]() by studying one interval of length
by studying one interval of length ![]() , say
, say ![]() .[4] For this reason, when graphing sine (and cosine) functions, we typically restrict our attention to graphing these functions over the course of one period to produce one cycle of the graph.
.[4] For this reason, when graphing sine (and cosine) functions, we typically restrict our attention to graphing these functions over the course of one period to produce one cycle of the graph.
Not surprisingly, the graph of ![]() exhibits similar behavior as
exhibits similar behavior as ![]() .[5]
.[5]
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|} \hline t & \cos(t) & (t,\cos(t)) \\ \hline 0 & 1 & (0, 1) \\ [2pt] \hline \frac{\pi}{4} & \frac{\sqrt{2}}{2} & \left(\frac{\pi}{4}, \frac{\sqrt{2}}{2}\right) \\ [2pt] \hline \frac{\pi}{2} & 0 & \left(\frac{\pi}{2}, 0\right) \\ [2pt] \hline \frac{3\pi}{4} & -\frac{\sqrt{2}}{2} & \left(\frac{3\pi}{4}, -\frac{\sqrt{2}}{2}\right) \\ [2pt] \hline \pi & -1 & (\pi, -1) \\ [2pt] \hline \frac{5\pi}{4} & -\frac{\sqrt{2}}{2} & \left(\frac{5\pi}{4}, -\frac{\sqrt{2}}{2}\right) \\ [2pt] \hline \frac{3\pi}{2} & 0 & \left(\frac{3\pi}{2}, 0 \right) \\ [2pt] \hline \frac{7\pi}{4} & \frac{\sqrt{2}}{2} & \left(\frac{7\pi}{4}, \frac{\sqrt{2}}{2}\right) \\ [2pt] \hline 2\pi & 1 & (2\pi, 1) \\ [2pt] \hline \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-21ad96b4b2a2ab9d93e8549bbe153534_l3.png)
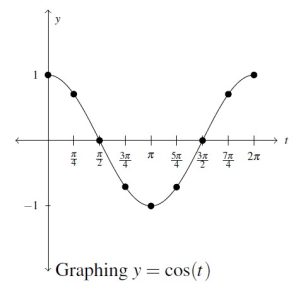
Like ![]() ,
, ![]() is a wavelike curve with period
is a wavelike curve with period ![]() . Moreover, the graphs of the sine and cosine functions have the same shape – differing only in what appears to be a horizontal shift. As we’ll prove in Section 8.2,
. Moreover, the graphs of the sine and cosine functions have the same shape – differing only in what appears to be a horizontal shift. As we’ll prove in Section 8.2, ![]() , which means we can obtain the graph of
, which means we can obtain the graph of ![]() by shifting the graph of
by shifting the graph of ![]() to the left
to the left ![]() units.[6]
units.[6]
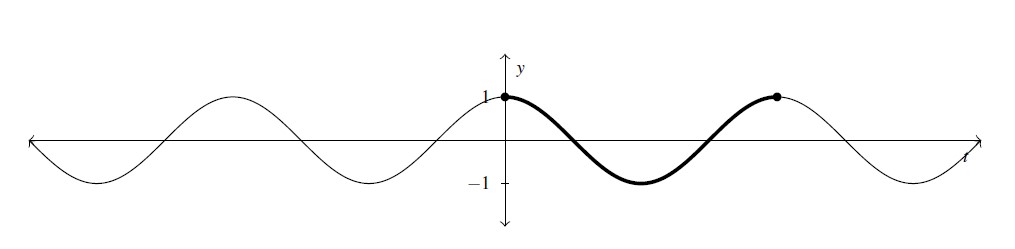
While arguably the most important property shared by ![]() and
and ![]() is their periodic `wavelike’ nature,[7] their graphs suggest these functions are both continuous and smooth. Recall from Section 2.2 that, like polynomial functions, the graphs of the sine and cosine functions have no jumps, gaps, holes in the graph, vertical asymptotes, corners or cusps.
is their periodic `wavelike’ nature,[7] their graphs suggest these functions are both continuous and smooth. Recall from Section 2.2 that, like polynomial functions, the graphs of the sine and cosine functions have no jumps, gaps, holes in the graph, vertical asymptotes, corners or cusps.
Moreover, the graphs of both ![]() and
and ![]() meander and never `settle down’ as
meander and never `settle down’ as ![]() to any one real number. So even though these functions are `trapped’ (or bounded) between
to any one real number. So even though these functions are `trapped’ (or bounded) between ![]() and
and ![]() , neither graph has any horizontal asymptotes.
, neither graph has any horizontal asymptotes.
Lastly, the graphs of ![]() and
and ![]() suggest each enjoy one of the symmetries introduced in Section 2.2. The graph of
suggest each enjoy one of the symmetries introduced in Section 2.2. The graph of ![]() appears to be symmetric about the origin while the graph of
appears to be symmetric about the origin while the graph of ![]() appears to be symmetric about the
appears to be symmetric about the ![]() -axis. Indeed, as we’ll prove in Section 8.2,
-axis. Indeed, as we’ll prove in Section 8.2, ![]() is, in fact, an odd function: [8] that is,
is, in fact, an odd function: [8] that is, ![]() and
and ![]() is an even function, so
is an even function, so ![]() .
.
We summarize all of these properties in the following result.
Theorem 7.6 Properties of the Sine and Cosine Functions
- The function
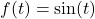
- has domain
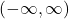
- has range
![Rendered by QuickLaTeX.com [-1,1]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-01968fac04e5065aa6fb740566b7905b_l3.png)
- is continuous and smooth
- is odd
- has period
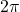
- has domain
- The function
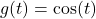
- has domain
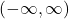
- has range
![Rendered by QuickLaTeX.com [-1,1]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-01968fac04e5065aa6fb740566b7905b_l3.png)
- is continuous and smooth
- is even
- has period
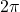
- has domain
- Conversion formulas:
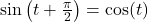 and
and 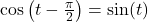
Now that we know the basic shapes of the graphs of ![]() and
and ![]() , we can use the results of Section 1.6 to graph more complicated functions using transformations. As mentioned already, the fact that both of these functions are periodic means we only have to know what happens over the course of one period of the function in order to determine what happens to all points on the graph. To that end, we graph the `fundamental cycle‘, the portion of each graph generated over the interval
, we can use the results of Section 1.6 to graph more complicated functions using transformations. As mentioned already, the fact that both of these functions are periodic means we only have to know what happens over the course of one period of the function in order to determine what happens to all points on the graph. To that end, we graph the `fundamental cycle‘, the portion of each graph generated over the interval ![]() , for each of the sine and cosine functions below.
, for each of the sine and cosine functions below.

In working through Section 1.6, it was very helpful to track `key points’ through the transformations. The `key points’ we’ve indicated on the graphs above correspond to the quadrantal angles and generate the zeros and the extrema of functions. Due to the fact that the quadrantal angles divide the interval ![]() into four equal pieces, we shall refer to these angles henceforth as the `quarter marks.’
into four equal pieces, we shall refer to these angles henceforth as the `quarter marks.’
It is worth noting that because the transformations discussed in Section 1.6 are linear,[9] the relative spacing of the points before and after the transformations remains the same.[10] In particular, wherever the interval ![]() is mapped, the quarter marks of the new interval correspond to the quarter marks of
is mapped, the quarter marks of the new interval correspond to the quarter marks of ![]() . (Can you see why?) We will exploit this fact in the following example.
. (Can you see why?) We will exploit this fact in the following example.
Example 7.3.1
Example 7.3.1.1
Graph one cycle of the following functions. State the period of each.
![]()
Solution:
Graph one cycle of ![]() .
.
One way to proceed is to use Theorem 1.12 and follow the procedure outlined there.
Starting with the fundamental cycle of ![]() , we divide each
, we divide each ![]() -coordinate by
-coordinate by ![]() and multiply each
and multiply each ![]() -coordinate by 3 to obtain one cycle of
-coordinate by 3 to obtain one cycle of ![]() .
.
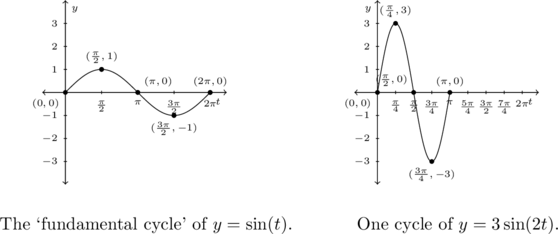
As a result of one cycle of ![]() being completed over the interval
being completed over the interval ![]() , the period of
, the period of ![]() is
is ![]() .
.
Example 7.3.1.2
Graph one cycle of the following functions. State the period of each.
![]()
Solution:
Graph one cycle of ![]() .
.
Starting with the fundamental cycle of ![]() and using Theorem 1.12, we subtract
and using Theorem 1.12, we subtract ![]() from each of the
from each of the ![]() -coordinates, then multiply each
-coordinates, then multiply each ![]() -coordinate by
-coordinate by ![]() , and add
, and add ![]() to each
to each ![]() -coordinate.
-coordinate.
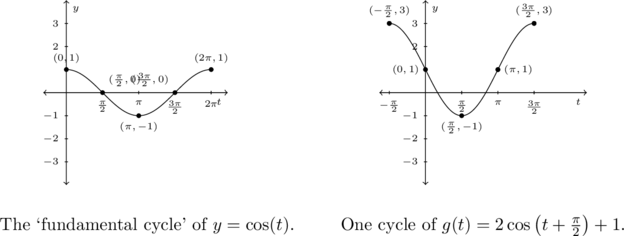
We find one cycle of ![]() is completed over the interval
is completed over the interval ![]() , the period is
, the period is ![]() .
.
As previously mentioned, the curves graphed in Example 7.3.1 are examples of sinusoids. A sinusoid is the result of taking the graph of ![]() or
or ![]() and performing any of the transformations mentioned in Section 1.6. We graph one cycle of a generic sinusoid below. Sinusoids can be characterized by four properties: period, phase shift, vertical shift (or `baseline’), and amplitude.
and performing any of the transformations mentioned in Section 1.6. We graph one cycle of a generic sinusoid below. Sinusoids can be characterized by four properties: period, phase shift, vertical shift (or `baseline’), and amplitude.
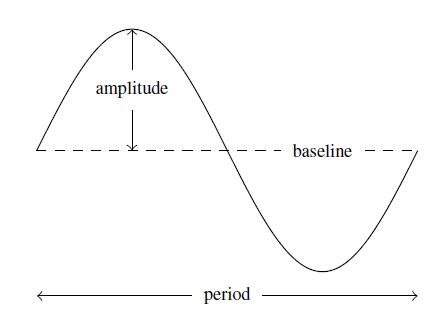
We have already discussed the period of a sinusoid. If we think of ![]() as measuring time, the period is how long it takes for the sinusoid to complete one cycle and is usually represented by the letter
as measuring time, the period is how long it takes for the sinusoid to complete one cycle and is usually represented by the letter ![]() . The standard period of both
. The standard period of both ![]() and
and ![]() is
is ![]() , but horizontal scalings will change this.
, but horizontal scalings will change this.
In Example 7.3.1, for instance, the function ![]() has period
has period ![]() instead of
instead of ![]() because the graph is horizontally compressed by a factor of
because the graph is horizontally compressed by a factor of ![]() as compared to the graph of
as compared to the graph of ![]() . However, the period of
. However, the period of ![]() is the same as the period of
is the same as the period of ![]() ,
, ![]() , because there are no horizontal scalings.
, because there are no horizontal scalings.
The phase shift of the sinusoid is the horizontal shift. Again, thinking of ![]() as time, the phase shift of a sinusoid can be thought of as when the sinusoid `starts’ as compared to
as time, the phase shift of a sinusoid can be thought of as when the sinusoid `starts’ as compared to ![]() . Assuming there are no reflections across the
. Assuming there are no reflections across the ![]() -axis, we can determine the phase shift of a sinusoid by finding where the value
-axis, we can determine the phase shift of a sinusoid by finding where the value ![]() on the graph of
on the graph of ![]() or
or ![]() is mapped to under the transformations.
is mapped to under the transformations.
For ![]() , the phase shift is `
, the phase shift is `![]() ‘ because the value
‘ because the value ![]() on the graph of
on the graph of ![]() remains stationary under the transformations. Loosely speaking, this means both
remains stationary under the transformations. Loosely speaking, this means both ![]() and
and ![]() `start’ at the same time. The phase shift of
`start’ at the same time. The phase shift of ![]() is
is ![]() or `
or `![]() to the left‘ because the value
to the left‘ because the value ![]() on the graph of
on the graph of ![]() is mapped to
is mapped to ![]() on the graph of
on the graph of ![]() . Again, loosely speaking, this means
. Again, loosely speaking, this means ![]() starts
starts ![]() time units earlier than
time units earlier than ![]()
The vertical shift of a sinusoid is exactly the same as the vertical shifts in Section 1.6 and determines the new `baseline’ of the sinusoid. Thanks to symmetry, the vertical shift can always be found by averaging the maximum and minimum values of the sinusoid. For ![]() , the vertical shift is
, the vertical shift is ![]() whereas the vertical shift of
whereas the vertical shift of ![]() is
is ![]() or `
or `![]() up.’
up.’
The amplitude of the sinusoid is a measure of how `tall’ the wave is, as indicated in the figure below. Said differently, the amplitude measures how much the curve gets displaced from its `baseline. ‘ The amplitude of the standard cosine and sine functions is ![]() , but vertical scalings can alter this.
, but vertical scalings can alter this.
In Example 7.3.1, the amplitude of ![]() is
is ![]() , owing to the vertical stretch by a factor of
, owing to the vertical stretch by a factor of ![]() as compared with the graph of
as compared with the graph of ![]() . In the case of
. In the case of ![]() , the amplitude is
, the amplitude is ![]() due to its vertical stretch as compared with the graph of
due to its vertical stretch as compared with the graph of ![]() . Note that the `
. Note that the `![]() ‘ here does not affect the amplitude of the curve; it merely changes the `baseline’ from
‘ here does not affect the amplitude of the curve; it merely changes the `baseline’ from ![]() to
to ![]() .
.
The following theorem shows how these four fundamental quantities relate to the parameters which describe a generic sinusoid. The proof follows from Theorem 1.12 and is left to the reader in Exercise 31.
Theorem 7.7
For ![]() , the graphs of
, the graphs of
![]()
- have frequency of
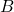
- have period
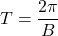
- have amplitude
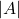
- have phase shift
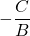
- have vertical shift or `baseline’
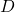
We put Theorem 7.7 to good use in the next example.
Example 7.3.2
Example 7.3.2.1
Use Theorem 7.7 to determine the frequency, period, phase shift, amplitude, and vertical shift of each of the following functions and use this information to graph one cycle of each function.
![]()
Solution:
Determine the frequency, period, phase shift, amplitude, and vertical shift of ![]() and then graph on cycle of the function.
and then graph on cycle of the function.
To use Theorem 7.7, we first need to rewrite ![]() in the form prescribed by Theorem 7.7. To that end, we rewrite:
in the form prescribed by Theorem 7.7. To that end, we rewrite: ![]() .
.
From this, we identify ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
According to Theorem 7.7, the frequency is ![]() , the period is
, the period is ![]() , the phase shift is
, the phase shift is ![]() (indicating a shift to the right
(indicating a shift to the right ![]() unit), the amplitude is
unit), the amplitude is ![]() , and the vertical shift is
, and the vertical shift is ![]() (indicating a shift up
(indicating a shift up ![]() unit.)
unit.)
To graph ![]() , we know one cycle begins at
, we know one cycle begins at ![]() (the phase shift.) Because the period is
(the phase shift.) Because the period is ![]() , we know the cycle ends
, we know the cycle ends ![]() units later at
units later at ![]() . If we divide the interval
. If we divide the interval ![]() into four equal pieces, each piece has length
into four equal pieces, each piece has length ![]() . Hence, we to get our quarter marks, we start with
. Hence, we to get our quarter marks, we start with ![]() and add
and add ![]() unit until we reach the endpoint,
unit until we reach the endpoint, ![]() . Our new quarter marks are:
. Our new quarter marks are: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]()
We now substitute these new quarter marks into ![]() to obtain the corresponding
to obtain the corresponding ![]() -values on the graph.[11] We connect the dots in a `wavelike’ fashion to produce the graph on the right.
-values on the graph.[11] We connect the dots in a `wavelike’ fashion to produce the graph on the right.
Note that we can (partially) spot-check our answer by noting the average of the maximum and minimum is ![]() (our vertical shift) and the amplitude,
(our vertical shift) and the amplitude, ![]() is indeed
is indeed ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|} \hline t & f(t) & (t,f(t)) \\ [2pt] \hline 1 & 4 & (1,4) \\ [2pt] \hline 2 & 1 & (2,1) \\ [2pt] \hline 3 & -2 & (3,-2) \\ [2pt] \hline 4 & 1 & (4,1) \\ [2pt] \hline 5 & 4 & (5,4) \\ [2pt] \hline \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-dca21a19f6278bcb36e988be051d69d9_l3.png)
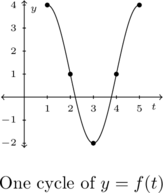
Thought not asked for, this example provides a nice opportunity to interpret the ordinary frequency: ![]() . Hence,
. Hence, ![]() of the sinusoid is traced out over an interval that is
of the sinusoid is traced out over an interval that is ![]() unit long.
unit long.
Example 7.3.2.2
Use Theorem 7.7 to determine the frequency, period, phase shift, amplitude, and vertical shift of each of the following functions and use this information to graph one cycle of each function.
![]()
Solution:
Determine the frequency, period, phase shift, amplitude, and vertical shift of ![]() and then graph on cycle of the function.
and then graph on cycle of the function.
Turning our attention now to the function ![]() , we first note that the coefficient of
, we first note that the coefficient of ![]() is negative. In order to use Theorem 7.7, we need that coefficient to be positive. Hence, we first use the odd property of the sine function to rewrite
is negative. In order to use Theorem 7.7, we need that coefficient to be positive. Hence, we first use the odd property of the sine function to rewrite ![]() so that instead of a coefficient of
so that instead of a coefficient of ![]() ,
, ![]() has a coefficient of
has a coefficient of ![]() . We get
. We get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \sin(\pi-2t) &=& \sin(-2t+\pi) \\ &=& \sin(- (2t-\pi)) \\ &=& -\sin(2t-\pi) \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-27da66dbdd2988c1a737f59b45644149_l3.png)
Hence, ![]()
We identify ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
The frequency is ![]() , the period is
, the period is ![]() , the phase shift is
, the phase shift is ![]() (indicating a shift right
(indicating a shift right ![]() units), the amplitude is
units), the amplitude is ![]() , and, finally, the vertical shift is up
, and, finally, the vertical shift is up ![]()
Proceeding as before, we know one cycle of ![]() starts at
starts at ![]() and ends at
and ends at ![]() . Dividing the interval
. Dividing the interval ![]() into four equal pieces gives pieces of length
into four equal pieces gives pieces of length ![]() units. Hence, to obtain our new quarter marks, we start at
units. Hence, to obtain our new quarter marks, we start at ![]() and add
and add ![]() until we reach
until we reach ![]() . Our new quarter marks are:
. Our new quarter marks are: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Substituting these values into
. Substituting these values into ![]() gives us the points to plot to produce the graph below on the right.
gives us the points to plot to produce the graph below on the right.
Again, we can quickly check the vertical shift by averaging the maximum and minimum values: ![]() and verify the amplitude:
and verify the amplitude: ![]()
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|} \hline t & g(t) & (t,g(t)) \\ [2pt] \hline \frac{\pi}{2} & \frac{3}{2} & \left(\frac{\pi}{2}, \frac{3}{2}\right) \\ [2pt] \hline \frac{3\pi}{4} & 1 & \left(\frac{3\pi}{4} , 1 \right) \\ [2pt] \hline \pi & \frac{3}{2} & \left(\pi , \frac{3}{2} \right) \\ [2pt] \hline \frac{5\pi}{4} & 2 & \left(\frac{5\pi}{4} , 2 \right) \\ [2pt] \hline \frac{3\pi}{2} & \frac{3}{2} & \left(\frac{3\pi}{2}, \frac{3}{2} \right) \\ [2pt] \hline \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c98b9dd57c57d9bfbeb0b27aa00e479e_l3.png)
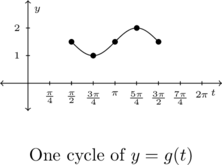
Note that in this section, we have discussed two ways to graph sinusoids: using Theorem 1.12 from Section 1.6 and using Theorem 7.7. Both methods will produce one cycle of the resulting sinusoid, but each method may produce a different cycle of the same sinusoid.
For example, if we graphed the function ![]() from Example 7.3.2 using Theorem 1.12, we obtain the following:
from Example 7.3.2 using Theorem 1.12, we obtain the following:
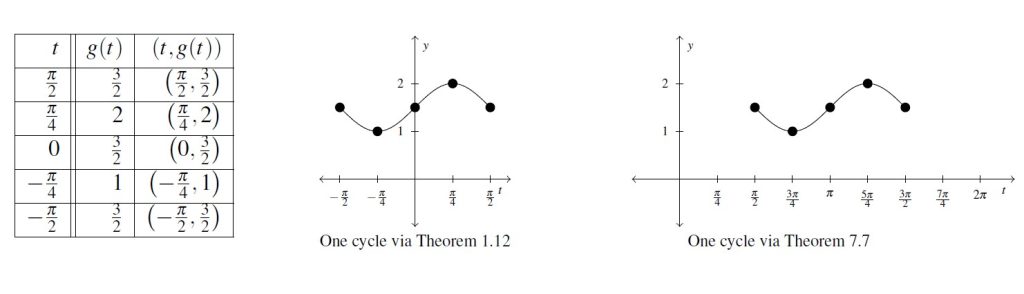
Comparing this result with the one obtained in Example 7.3.2 side by side, we see that one cycle ends right where the other starts. The cause of this discrepancy goes back to using the odd property of sine.
Essentially, the odd property of the sine function converts a reflection across the ![]() -axis into a reflection across the
-axis into a reflection across the ![]() -axis. (Can you see why?) For this reason, whenever the coefficient of
-axis. (Can you see why?) For this reason, whenever the coefficient of ![]() is negative, Theorems 1.12 and 7.7 will produce different results.
is negative, Theorems 1.12 and 7.7 will produce different results.
In the Exercises, we assume the problems are worked using Theorem 7.7. If you choose to use Theorems 1.12 instead, your answer may look different than what is provided even though both your answer and the textbook’s answer represent one cycle of the same function.
In the next example, we use Theorem 7.7 to determine the formula of a sinusoid given the graph of one cycle. Note that in some disciplines, sinusoids are written in terms of sines whereas in others, cosines functions are preferred. To cover all bases, we ask for both.
Example 7.3.3
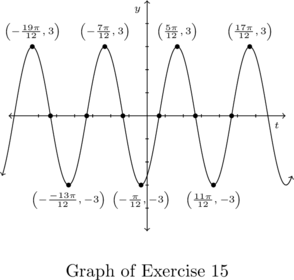
Example 7.3.3.1
Below is the graph of one complete cycle of a sinusoid ![]() .
.
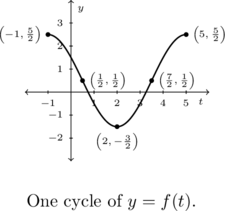
Write ![]() in the form
in the form ![]() , for
, for ![]() .
.
Solution:
Write ![]() in the form
in the form ![]() , for
, for ![]() .
.
One cycle is graphed over the interval ![]() , thus its period is
, thus its period is ![]() .
.
According to Theorem 7.7, ![]() , so that
, so that ![]() .
.
Next, we see that the phase shift is ![]() , so we have
, so we have ![]() , or
, or ![]() .
.
To find the baseline, we average the maximum and minimum values: ![]() .
.
To find the amplitude, we subtract the maximum value from the baseline: ![]() .
.
Putting this altogether, we obtain our final answer is ![]() .
.
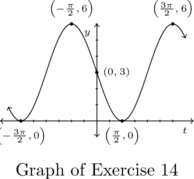
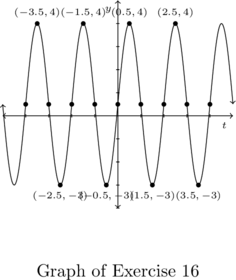
Example 7.3.3.2
Below is the graph of one complete cycle of a sinusoid ![]() .
.

Write ![]() in the form
in the form ![]() , for
, for ![]() .
.
Solution:
Write ![]() in the form
in the form ![]() , for
, for ![]() .
.
Because we have written ![]() in terms of cosines, we can use the conversion from sine to cosine as listed in Theorem 7.6.
in terms of cosines, we can use the conversion from sine to cosine as listed in Theorem 7.6.
As ![]() ,
, ![]() , so
, so ![]() .
.
Our final answer is ![]() .
.
However, for the sake of completeness, we provide another solution strategy which enables us to write ![]() in terms of sines without starting with our answer from part 1.
in terms of sines without starting with our answer from part 1.
Note that we obtain the period, amplitude, and vertical shift as before: ![]() ,
, ![]() and
and ![]() . The trickier part is finding the phase shift.
. The trickier part is finding the phase shift.
To that end, we imagine extending the graph of the given sinusoid as in the figure below so that we can identify a cycle beginning at ![]() . Taking the phase shift to be
. Taking the phase shift to be ![]() , we get
, we get ![]() , or
, or ![]()
Hence, our answer is ![]()
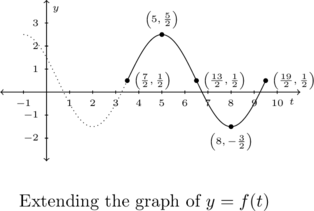
Note that each of the answers given in Example 7.3.3 is one choice out of many possible answers. For example, when fitting a sine function to the data, we could have chosen to start at ![]() taking
taking ![]() . In this case, the phase shift is
. In this case, the phase shift is ![]() so
so ![]() for an answer of
for an answer of ![]() . The ultimate check of any solution is to graph the answer and check it matches the given data.
. The ultimate check of any solution is to graph the answer and check it matches the given data.
7.3.1 Applications of Sinusoids
In the same way exponential functions can be used to model a wide variety of phenomena in nature,[12] the sine and cosine functions can be used to model their fair share of natural behaviors. Our first foray into sinusoidal motion revisits circular motion – in particular Equation 7.3.
Example 7.3.4
Example 7.3.4
Recall from Exercise 55 in Section 7.1.2 that The Giant Wheel at Cedar Point is a circle with diameter 128 feet which sits on an 8 foot tall platform making its overall height 136 feet. It completes two revolutions in 2 minutes and 7 seconds. Assuming that the riders are at the edge of the circle, find a sinusoid which describes the height of the passengers above the ground ![]() seconds after they pass the point on the wheel closest to the ground.
seconds after they pass the point on the wheel closest to the ground.
Solution:
We sketch the problem situation below and assume a counter-clockwise rotation.[13]

We know from the equations given on Circular Motion in Section 7.2.3 that the ![]() -coordinate for counter-clockwise motion on a circle of radius
-coordinate for counter-clockwise motion on a circle of radius ![]() centered at the origin with constant angular velocity (frequency)
centered at the origin with constant angular velocity (frequency) ![]() is given by
is given by ![]() . Here,
. Here, ![]() corresponds to the point
corresponds to the point ![]() so that
so that ![]() , the angle measuring the amount of rotation, is in standard position.
, the angle measuring the amount of rotation, is in standard position.
In our case, the diameter of the wheel is 128 feet, so the radius is ![]() feet. Because the wheel completes two revolutions in 2 minutes and 7 seconds (which is
feet. Because the wheel completes two revolutions in 2 minutes and 7 seconds (which is ![]() seconds) the period
seconds) the period ![]() seconds. Hence, the frequency is
seconds. Hence, the frequency is ![]() radians per second.
radians per second.
Putting these two pieces of information together, we have that ![]() describes the
describes the ![]() -coordinate on the Giant Wheel after
-coordinate on the Giant Wheel after ![]() seconds, assuming it is centered at
seconds, assuming it is centered at ![]() with
with ![]() corresponding to point
corresponding to point ![]() .
.
In order to find an expression for ![]() , we take the point
, we take the point ![]() in the figure as the origin. As the base of the Giant Wheel ride is
in the figure as the origin. As the base of the Giant Wheel ride is ![]() feet above the ground and the Giant Wheel itself has a radius of
feet above the ground and the Giant Wheel itself has a radius of ![]() feet, its center is
feet, its center is ![]() feet above the ground. To account for this vertical shift upward,[14] we add
feet above the ground. To account for this vertical shift upward,[14] we add ![]() to our formula for
to our formula for ![]() to obtain the new formula
to obtain the new formula ![]()
Next, we need to adjust things so that ![]() corresponds to the point
corresponds to the point ![]() instead of the point
instead of the point ![]() . This is where the phase comes into play. Geometrically, we need to shift the angle
. This is where the phase comes into play. Geometrically, we need to shift the angle ![]() in the figure back
in the figure back ![]() radians.
radians.
From the discussion on circular motion, we know ![]() , so we (temporarily) write the height in terms of
, so we (temporarily) write the height in terms of ![]() as
as ![]() . Subtracting
. Subtracting ![]() from
from ![]() gives
gives
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(t) &=& 64 \sin\left(\theta - \frac{\pi}{2}\right) + 72 \\[6pt] &=& 64\sin\left(\frac{4 \pi}{127} t -\frac{\pi}{2} \right) + 72 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e1111e8289abe6799eb9bea14367ef79_l3.png)
We can check the reasonableness of our answer by graphing ![]() over the interval
over the interval ![]() and visualizing the path of a person on the Big Wheel ride over the course of one rotation.
and visualizing the path of a person on the Big Wheel ride over the course of one rotation.
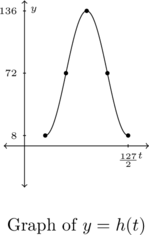
A few remarks about Example 7.3.4 are in order. First, note that the amplitude of ![]() in our answer corresponds to the radius of the Giant Wheel. This means that passengers on the Giant Wheel never stray more than
in our answer corresponds to the radius of the Giant Wheel. This means that passengers on the Giant Wheel never stray more than ![]() feet vertically from the center of the Wheel, which makes sense. Second, the phase shift of our answer works out to be
feet vertically from the center of the Wheel, which makes sense. Second, the phase shift of our answer works out to be ![]() . This represents the `time delay’ (in seconds) we introduce by starting the motion at the point
. This represents the `time delay’ (in seconds) we introduce by starting the motion at the point ![]() as opposed to the point
as opposed to the point ![]() . Said differently, passengers which `start’ at
. Said differently, passengers which `start’ at ![]() take
take ![]() seconds to `catch up’ to the point
seconds to `catch up’ to the point ![]()
7.3.2 Section Exercises
In Exercises 1 – 12, graph one cycle of the given function. State the period, amplitude, phase shift and vertical shift of the function.
In Exercises 13 – 16, a sinusoid is graphed. Write a formula for the sinusoid in the form ![]() and
and ![]() . Select
. Select ![]() so
so ![]() . Check your answer by graphing.
. Check your answer by graphing.
-
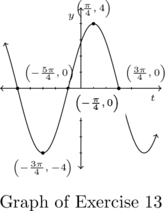
-
-
-
- Use the graph of
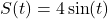 to graph each of the following functions. State the period of each.
to graph each of the following functions. State the period of each.
In Exercises 18 – 23, use a graphing utility to graph each function and discuss the related questions with your classmates.
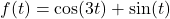 . Is this function periodic? If so, what is the period?
. Is this function periodic? If so, what is the period?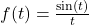 . What appears to be the horizontal asymptote of the graph?
. What appears to be the horizontal asymptote of the graph?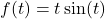 . Graph
. Graph  . What do you notice?
. What do you notice?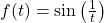 . What’s happening as
. What’s happening as 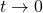 ?
?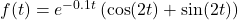 . Graph
. Graph 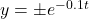 on the same set of axes. What do you notice?
on the same set of axes. What do you notice?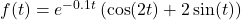 . Graph
. Graph 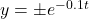 on the same set of axes. What do you notice?
on the same set of axes. What do you notice?- Show every constant function
 is periodic by explaining why
is periodic by explaining why 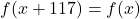 for all real numbers
for all real numbers 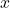 . Then show that
. Then show that  has no period by showing that you cannot find a smallest number
has no period by showing that you cannot find a smallest number 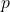 such that
such that 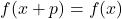 for all real numbers
for all real numbers 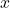 .Said differently, show that
.Said differently, show that 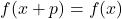 for all real numbers
for all real numbers 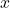 for ALL values of
for ALL values of 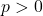 , so no smallest value exists to satisfy the definition of `period’.
, so no smallest value exists to satisfy the definition of `period’. - The sounds we hear are made up of mechanical waves. The note `A’ above the note `middle C’ is a sound wave with ordinary frequency
 Hertz
Hertz 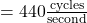 . Find a sinusoid which models this note, assuming that the amplitude is
. Find a sinusoid which models this note, assuming that the amplitude is 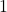 and the phase shift is
and the phase shift is 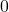 .
. - The voltage
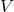 in an alternating current source has amplitude
in an alternating current source has amplitude 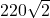 and ordinary frequency
and ordinary frequency 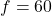 Hertz. Find a sinusoid which models this voltage. Assume that the phase is
Hertz. Find a sinusoid which models this voltage. Assume that the phase is 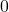 .
. - The London Eye is a popular tourist attraction in London, England and is one of the largest Ferris Wheels in the world. It has a diameter of 135 meters and makes one revolution (counter-clockwise) every 30 minutes. It is constructed so that the lowest part of the Eye reaches ground level, enabling passengers to simply walk on to, and off of, the ride. Find a sinusoid which models the height
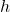 of the passenger above the ground in meters
of the passenger above the ground in meters 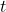 minutes after they board the Eye at ground level.
minutes after they board the Eye at ground level. - In Section 7.2.3, we found the
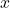 -coordinate of counter-clockwise motion on a circle of radius
-coordinate of counter-clockwise motion on a circle of radius  with angular frequency
with angular frequency 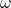 to be
to be  , where
, where 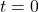 corresponds to the point
corresponds to the point 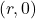 . Suppose we are in the situation of Exercise 27 above. Find a sinusoid which models the horizontal displacement
. Suppose we are in the situation of Exercise 27 above. Find a sinusoid which models the horizontal displacement 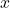 of the passenger from the center of the Eye in meters
of the passenger from the center of the Eye in meters 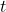 minutes after they board the Eye. Here we take
minutes after they board the Eye. Here we take 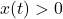 to mean the passenger is to the right of the center, while
to mean the passenger is to the right of the center, while 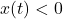 means the passenger is to the left of the center.
means the passenger is to the left of the center. - In Exercise 52 in Section 7.1.2, we introduced the yo-yo trick `Around the World’ in which a yo-yo is thrown so it sweeps out a vertical circle. As in that exercise, suppose the yo-yo string is 28 inches and it completes one revolution in 3 seconds. If the closest the yo-yo ever gets to the ground is 2 inches, find a sinusoid which models the height
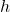 of the yo-yo above the ground in inches
of the yo-yo above the ground in inches 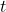 seconds after it leaves its lowest point.
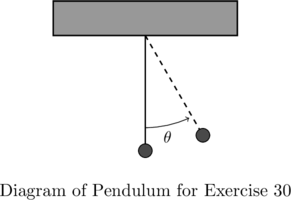
seconds after it leaves its lowest point. - Consider the pendulum below. Ignoring air resistance, the angular displacement of the pendulum from the vertical position,
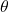 , can be modeled as a sinusoid.[15]
, can be modeled as a sinusoid.[15]
The amplitude of the sinusoid is the same as the initial angular displacement,
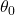 , of the pendulum and the period of the motion is given by
, of the pendulum and the period of the motion is given by![Rendered by QuickLaTeX.com \[T = 2\pi \sqrt{\dfrac{\ell}{g}}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-609bc3120c0da8d7ae8a8e516e5b8449_l3.png)
where
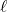 is the length of the pendulum and
is the length of the pendulum and 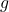 is the acceleration due to gravity.
is the acceleration due to gravity.- Find a sinusoid which gives the angular displacement
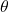 as a function of time,
as a function of time, 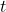 . Arrange things so
. Arrange things so 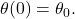
- In Exercise 24 Section 4.1, you found the length of the pendulum needed in Jeff’s antique Seth-Thomas clock to ensure the period of the pendulum is
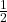 of a second. Assuming the initial displacement of the pendulum is
of a second. Assuming the initial displacement of the pendulum is 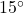 , find a sinusoid which models the displacement of the pendulum
, find a sinusoid which models the displacement of the pendulum 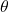 as a function of time,
as a function of time, 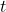 , in seconds.
, in seconds.
- Find a sinusoid which gives the angular displacement
- Use Theorem 1.12 to prove Theorem 7.7.
Section 7.3 Exercise Answers can be found in the Appendix … Coming soon
- which, you'll recall essentially `wraps the real number line around the Unit Circle ↵
- in particular the interval
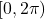 ↵
↵ - Keep in mind that we're using `
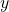 ' here to denote the output from the sine function. It is a coincidence that the
' here to denote the output from the sine function. It is a coincidence that the 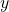 -values on the graph of
-values on the graph of 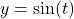 correspond to the
correspond to the 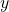 -values on the Unit Circle. ↵
-values on the Unit Circle. ↵ - Technically, we should study the interval
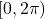 , (In some advanced texts, the interval of choice is
, (In some advanced texts, the interval of choice is 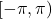 ) as whatever happens at
) as whatever happens at 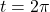 is the same as what happens at
is the same as what happens at 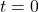 . As we will see shortly,
. As we will see shortly, 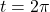 gives us an extra `check' when we go to graph these functions. ↵
gives us an extra `check' when we go to graph these functions. ↵ - Here note that the dependent variable `
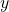 ' represents the outputs from
' represents the outputs from 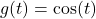 which are
which are 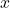 -coordinates on the Unit Circle. ↵
-coordinates on the Unit Circle. ↵ - Hence, we can obtain the graph of
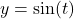 by shifting the graph of
by shifting the graph of 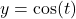 to the right
to the right 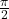 units:
units: 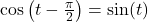 . ↵
. ↵ - this is the reason they are so useful in the Sciences and Engineering ↵
- The reader may wish to review Definitions 2.5 and 2.6 as needed. ↵
- See the remarks at the beginning of Section 1.6. ↵
- If we use a linear function
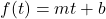 to transform the inputs,
to transform the inputs, 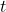 , then
, then ![Rendered by QuickLaTeX.com \Delta[f(t)] = m \Delta t](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3c9a0f10c6a673046985e3183e2e0ae7_l3.png) . That is, the change after the transformation,
. That is, the change after the transformation, 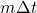 , is just a multiple of the change before the transformation,
, is just a multiple of the change before the transformation, 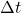 . ↵
. ↵ - Note when we substitute the quarter marks into
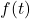 , the argument of the cosine function simplifies to the quadrantal angles. That is, when we substitute
, the argument of the cosine function simplifies to the quadrantal angles. That is, when we substitute 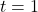 , the argument of cosine simplifies to
, the argument of cosine simplifies to 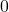 ; when we substitute
; when we substitute 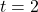 , the argument simplifies
, the argument simplifies 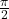 and so on. This provides a quick check of our calculations. ↵
and so on. This provides a quick check of our calculations. ↵ - See Section 5.7. ↵
- Otherwise, we could just observe the motion of the wheel from the other side. ↵
- We are readjusting our `baseline' from
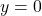 to
to 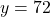 . ↵
. ↵ - Provided
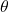 is kept `small.' Carl remembers the `Rule of Thumb' as being
is kept `small.' Carl remembers the `Rule of Thumb' as being 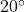 or less. Check with your friendly neighborhood physicist to make sure. ↵
or less. Check with your friendly neighborhood physicist to make sure. ↵
A graph having a wavelike nature.
A function were f(t+c)=f(t) for all t and a real number c.
The smallest positive number there the function repeats.
The portion of a trigonometric function's graph generated over the interval 0 to 2pi.
The horizontal shift of a sinusoid
The height of a sinusoid wave

