9.2 Dot Products and Projections
In Section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. In this section, we define a product of vectors. We begin with the following definition.
For example, if ![]() and
and ![]() ,then
,then
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{v} \cdot \vec{w} &=& \left<3,4\right> \cdot \left<1,-2\right>\\ &=& (3)(1) + (4)(-2) \\ &=& -5 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-943c7472a88d9d9ee05870540a5e7f8d_l3.png)
Note that the dot product takes two vectors and produces a scalar. For that reason, the quantity ![]() is often called the scalar product of
is often called the scalar product of ![]() and
and ![]() . The dot product enjoys the following properties.
. The dot product enjoys the following properties.
Theorem 9.5 Properties of the Dot Product
- Commutative Property: For all vectors
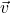 and
and 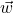 ,
, 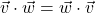
- Distributive Property: For all vectors
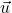 ,
, 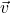 and
and 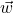 ,
, 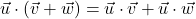
- Scalar Property: For all vectors
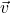 and
and 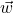 and scalars
and scalars 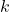 ,
, 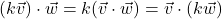
- Relation to Magnitude: For all vectors
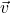 ,
, 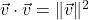
Like most of the theorems involving vectors, the proof of Theorem 9.5 amounts to using the definition of the dot product and properties of real number arithmetic.
For example, to show the commutative property, let ![]() and
and ![]() . Then
. Then
![Rendered by QuickLaTeX.com \[ \begin{array}{rcll} \vec{v} \cdot \vec{w} & = & \left<v_{1},v_{2}\right> \cdot \left<w_{1},w_{2}\right> & \\ [3pt] & = & v_{1}w_{1} + v_{2}w_{2} & \text{Definition of Dot Product} \\ [3pt] & = & w_{1}v_{1} + w_{2}v_{2} & \text{Commutativity of Real Number Multiplication} \\ [3pt] & = & \left<w_{1},w_{2}\right> \cdot \left<v_{1},v_{2}\right> & \text{Definition of Dot Product} \\ [3pt] & = & \vec{w} \cdot \vec{v} & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-354d5dbc34bba7637014d10ae7a0599c_l3.png)
The distributive property is proved similarly and is left as an exercise.
For the scalar property, assume that ![]() and
and ![]() and
and ![]() is a scalar. Then
is a scalar. Then
![Rendered by QuickLaTeX.com \[ \begin{array}{rcll} (k\vec{v}) \cdot \vec{w} & = & \left(k \left<v_{1},v_{2}\right> \right) \cdot \left<w_{1},w_{2}\right> & \\ [3pt] & = & \left<kv_{1},kv_{2}\right> \cdot \left<w_{1},w_{2}\right> & \text{Definition of Scalar Multiplication} \\ [3pt] & = & (kv_{1})(w_{1}) + (kv_{2})(w_{2}) & \text{Definition of Dot Product} \\ [3pt] & = & k(v_{1}w_{1}) + k(v_{2}w_{2}) & \text{Associativity of Real Number Multiplication} \\ [3pt] & = & k(v_{1}w_{1} + v_{2}w_{2}) & \text{Distributive Law of Real Numbers} \\ [3pt] & = & k \left<v_{1},v_{2}\right> \cdot \left<w_{1},w_{2}\right> & \text{Definition of Dot Product} \\ [3pt] & = & k (\vec{v} \cdot \vec{w}) & \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ddcaeb25e33c467bd59997699bb6b814_l3.png)
We leave the proof of ![]() as an exercise.
as an exercise.
For the last property, we note that if ![]() , then
, then ![]() , where the last equality comes courtesy of Definition 9.4.
, where the last equality comes courtesy of Definition 9.4.
The following example puts Theorem 9.5 to good use. As in Example 9.2.1, we work out the problem in great detail and encourage the reader to supply the justification for each step.
Example 9.2.1
Example 9.2.1
Prove the identity: ![]() .
.
Solution:
We begin by rewriting ![]() in terms of the dot product using Theorem 9.5.
in terms of the dot product using Theorem 9.5.
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \| \vec{v} - \vec{w} \|^2 & = & (\vec{v} - \vec{w}) \cdot (\vec{v} - \vec{w}) \\ [3pt] & = & (\vec{v} + [-\vec{w}]) \cdot (\vec{v} + [-\vec{w}]) \\ [3pt] & = & (\vec{v} + [-\vec{w}]) \cdot \vec{v} +(\vec{v} + [-\vec{w}]) \cdot [-\vec{w}] \\ [3pt] & = & \vec{v} \cdot (\vec{v} + [-\vec{w}]) + [-\vec{w}] \cdot (\vec{v} + [-\vec{w}]) \\ [3pt] & = & \vec{v} \cdot \vec{v} + \vec{v} \cdot [-\vec{w}] + [-\vec{w}]\cdot \vec{v} + [-\vec{w}]\cdot[-\vec{w}] \\ [3pt] & = & \vec{v} \cdot \vec{v} + \vec{v} \cdot [(-1)\vec{w}] + [(-1)\vec{w}]\cdot \vec{v} + [(-1)\vec{w}]\cdot[(-1)\vec{w}] \\ [3pt] & = & \vec{v} \cdot \vec{v} + (-1)(\vec{v} \cdot \vec{w}) + (-1)(\vec{w} \cdot \vec{v}) + [(-1)(-1)](\vec{w}\cdot\vec{w}) \\ [3pt] & = & \vec{v} \cdot \vec{v} + (-1)(\vec{v} \cdot \vec{w}) + (-1)(\vec{v} \cdot \vec{w}) + \vec{w}\cdot\vec{w} \\ [3pt] & = & \vec{v} \cdot \vec{v} -2(\vec{v} \cdot \vec{w}) + \vec{w}\cdot\vec{w} \\ [3pt] & = & \|\vec{v}\|^2-2(\vec{v} \cdot \vec{w}) + \|\vec{w}\|^2 \\ \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fb1fa81d9cfc5feb4488662a9d130070_l3.png)
Hence, ![]() as required.
as required.
If we take a step back from the pedantry in Example 9.2.1, we see that the bulk of the work is needed to show that ![]() . If this looks familiar, it should.
. If this looks familiar, it should.
As the dot product enjoys many of the same properties enjoyed by real numbers, the machinations required to expand ![]() for vectors
for vectors ![]() and
and ![]() match those required to expand
match those required to expand ![]() for real numbers
for real numbers ![]() and
and ![]() , and hence we get similar looking results.
, and hence we get similar looking results.
The identity verified in Example 9.2.1 plays a large role in the development of the geometric properties of the dot product, which we now explore.
Suppose ![]() and
and ![]() are two nonzero vectors. If we draw
are two nonzero vectors. If we draw ![]() and
and ![]() with the same initial point, we define the angle between
with the same initial point, we define the angle between ![]() and
and ![]() to be the angle
to be the angle ![]() determined by the rays containing the vectors
determined by the rays containing the vectors ![]() and
and ![]() , as illustrated below. We require
, as illustrated below. We require ![]() . (Think about why this is needed in the definition.)
. (Think about why this is needed in the definition.)
The following theorem gives us some insight into the geometric role the dot product plays.
Theorem 9.6 Geometric Interpretation of Dot Product
If ![]() and
and ![]() are nonzero vectors then
are nonzero vectors then
![]()
where ![]() is the angle between
is the angle between ![]() and
and ![]() .
.
We prove Theorem 9.6 in cases. If ![]() , then
, then ![]() and
and ![]() have the same direction. It follows[1] that there is a real number
have the same direction. It follows[1] that there is a real number ![]() such that
such that ![]() . Hence,
. Hence,
![]()
Working from the other end of the equation,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \| \vec{v} \| \| \vec{w} \| \cos(\theta) &=& \| \vec{v} \| \|k \vec{v} \| \cos(0) \\ &=& \| \vec{v} \| (|k| \| \vec{v} \|) (1) \\ &=& k \| \vec{v} \|^2 \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-65f22e4c06c630a399e3e85ecf2b5f61_l3.png)
where ![]() courtesy of Theorem 9.3, and
courtesy of Theorem 9.3, and ![]() because
because ![]()
Hence, in the case ![]() , we have shown
, we have shown ![]() and
and ![]() . Putting these two equations together shows that
. Putting these two equations together shows that
![]()
holds in this case.
If ![]() ,
, ![]() and
and ![]() have the exact opposite directions, so there is a real number
have the exact opposite directions, so there is a real number ![]() with
with ![]() .
.
As before, we compute ![]() . Because
. Because ![]() here, we have
here, we have ![]() . Hence, we find
. Hence, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \| \vec{v} \| \| \vec{w} \| \cos(\theta) &=& \| \vec{v} \| \| k \vec{v} \| \cos(\pi) \\ &=& \| \vec{v} \| (|k| \| \vec{v} \|) (-1) \\ &=& \| \vec{v} \| (-k) \| \vec{v} \| (-1)\\ &=& k \| \vec{v} \|^2 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-68dafdade9c6b224ae916e508031402d_l3.png)
Once again, both ![]() and
and ![]() , so
, so ![]() in this case.
in this case.
Next, if ![]() , the vectors
, the vectors ![]() ,
, ![]() and
and ![]() determine a triangle with side lengths
determine a triangle with side lengths ![]() ,
, ![]() and
and ![]() , respectively, as seen in the diagram below.
, respectively, as seen in the diagram below.

The Law of Cosines yields ![]() .
.
From Example 9.2.1, we also have that ![]()
Equating these two expressions for ![]() gives
gives
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \|\vec{v}\|^2 + \|\vec{w}\|^2 - 2\|\vec{v}\| \|\vec{w}\| \cos(\theta) &=& \|\vec{v}\|^2 -2 (\vec{v} \cdot \vec{w}) + \|\vec{w}\|^2 \\[4pt] - 2\|\vec{v}\| \|\vec{w}\| \cos(\theta) \\[4pt] &=& -2 (\vec{v} \cdot \vec{w}) \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-74056250b3d72b6bf1a256c42f30fd5e_l3.png)
Hence, ![]() , as required.
, as required.
An immediate consequence of Theorem 9.6 is the following.
We obtain the formula in Theorem 9.7 by solving the equation given in Theorem 9.6 for ![]()
As ![]() and
and ![]() are nonzero, so are
are nonzero, so are ![]() and
and ![]() . Hence, we may divide both sides of
. Hence, we may divide both sides of ![]() by
by ![]() . Given
. Given ![]() by definition, the values of
by definition, the values of ![]() exactly match the range of the arccosine function. Hence,
exactly match the range of the arccosine function. Hence,
![]()
Using Theorem 9.5, we can rewrite
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \frac{\vec{v} \cdot \vec{w}}{\| \vec{v} \| \|\vec{w} \|} &=& \left(\frac{1}{\|\vec{v}\|} \vec{v}\right) \cdot \left(\frac{1}{\|\vec{w}\|} \vec{w}\right) \\[10pt] &=& \bm\hat{v} \cdot \bm\hat{w} \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9f35f1ea326fa78d972b15a9b219e858_l3.png)
giving us the alternative formula listed in Theorem 9.7: ![]()
We are overdue for an example.
Example 9.2.2
Example 9.2.2.1
Compute the angle between the following pairs of vectors. Graph each pair of vectors in standard position to check the reasonableness of your answer.
![]() , and
, and ![]()
Solution:
We use the formula ![]() from Theorem 9.7 in each case below.
from Theorem 9.7 in each case below.
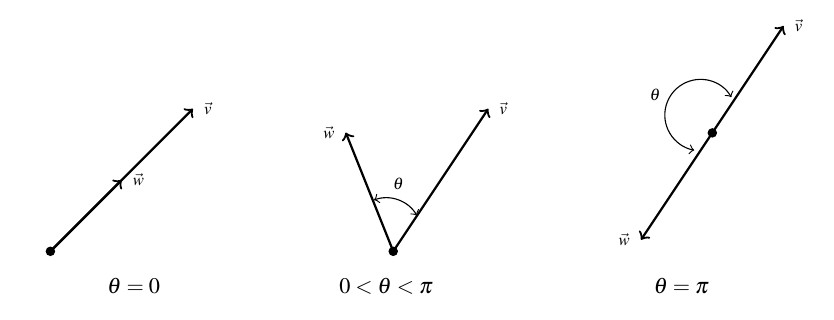
Compute the angle between ![]() , and
, and ![]()
We have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{v} \cdot \vec{w} &=& \left< 3, -3\sqrt{3} \right> \cdot \left<-\sqrt{3}, 1 \right> \\ & =& -3\sqrt{3} - 3\sqrt{3} \\ &=& -6\sqrt{3} \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-0cf051f5dc0f9e278a04ca2d2d5c90bc_l3.png)
Computing the length of each vector, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \| \vec{v} \| &=& \sqrt{3^2+(-3\sqrt{3})^2}\\[4pt] &=& \sqrt{36} \\[4pt] &=& 6 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3589d2c679b2bb768c9c7cb5a1f6afec_l3.png)
and
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \| \vec{w}\| &=& \sqrt{(-\sqrt{3})^2+1^2} \\[4pt] &=& \sqrt{4} \\[4pt] &=& 2 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-56d62a91f1de2406e77b61eca2897aae_l3.png)
Hence, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \theta &=& \arccos\left(\frac{-6\sqrt{3}}{12}\right) \\[4pt] &=& \arccos\left(-\frac{\sqrt{3}}{2}\right) \\[4pt] &=& \frac{5\pi}{6} \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f2f2ef39214964233975a45f4c13b6a9_l3.png)
We check our answer geometrically by graphing this pair of vectors.
 </p>
</p>
Example 9.2.2.2
Compute the angle between the following pairs of vectors. Graph each pair of vectors in standard position to check the reasonableness of your answer.
![]() , and
, and ![]()
Solution:
We use the formula ![]() from Theorem 9.7 in each case below.
from Theorem 9.7 in each case below.
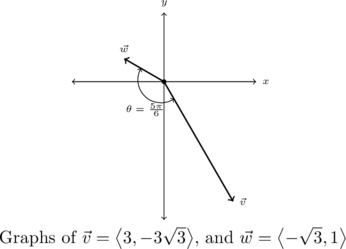
Compute the angle between ![]() , and
, and ![]() .
.
For ![]() and
and ![]() , we find
, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{v} \cdot \vec{w} &=& \left< 2, 2 \right> \cdot \left<5, -5\right>\\ &=& 10-10 \\ &=& 0 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f16ef2812b711081e3b6b574cf2d22c7_l3.png)
Hence, it doesn’t matter what ![]() and
and ![]() are,
are,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \theta &=& \arccos\left( \frac{\vec{v} \cdot \vec{w}}{\| \vec{v} \| \|\vec{w} \|}\right) \\[10pt] &=& \arccos(0) \\[4pt] &=& \frac{\pi}{2} \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-72c652a8fabf5a280a372768f022c950_l3.png)
We check our answer geometrically by graphing this pair of vectors.
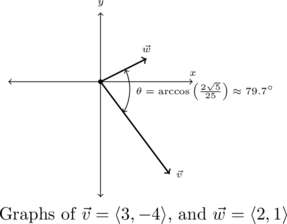
Example 9.2.2.3
Compute the angle between the following pairs of vectors. Graph each pair of vectors in standard position to check the reasonableness of your answer.
![]() , and
, and ![]()
Solution:
We use the formula ![]() from Theorem 9.7 in each case below.
from Theorem 9.7 in each case below.
Compute the angle between ![]() , and
, and ![]() .
.
We find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{v} \cdot \vec{w} &=& \left< 3, -4 \right> \cdot \left<2, 1\right>\\ &=& 6 - 4 \\ &=& 2 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8a42eb1bb6ecf05e7cb405fa28c97459_l3.png)
Computing lengths, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \| \vec{v} \| &=& \sqrt{3^2+(-4)^2}\\[4pt] &=& \sqrt{25} \\ &=& 5 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b35751ecd868f9d248754199a14e78e8_l3.png)
and
![]()
and as a result
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \theta &=& \arccos\left(\frac{2}{5\sqrt{5}}\right)\\[10pt] &=& \arccos\left(\frac{2\sqrt{5}}{25} \right) \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-188c440ec633d122e58f8c7d97cb3edf_l3.png)
As ![]() isn’t the cosine of one of the `common angles,’ we leave our exact answer in terms of the arccosine function. For the purposes of checking our answer, however, we approximate
isn’t the cosine of one of the `common angles,’ we leave our exact answer in terms of the arccosine function. For the purposes of checking our answer, however, we approximate ![]() .
.
A few remarks about Example 9.2.2 are in order. Note that for nonzero vectors ![]() and
and ![]() , the lengths
, the lengths ![]() and
and ![]() are always positive. Theorem 9.6 tells us that
are always positive. Theorem 9.6 tells us that ![]() , thus we know the sign of
, thus we know the sign of ![]() is the same as the sign of
is the same as the sign of ![]()
Geometrically, if ![]() , then
, then ![]() so
so ![]() is an obtuse angle, demonstrated in number 1 above.
is an obtuse angle, demonstrated in number 1 above.
If ![]() , then
, then ![]() so
so ![]() as in number 2. In this case, the vectors
as in number 2. In this case, the vectors ![]() and
and ![]() are called orthogonal. Geometrically, when orthogonal vectors are sketched with the same initial point, the lines containing the vectors are perpendicular. Hence, if
are called orthogonal. Geometrically, when orthogonal vectors are sketched with the same initial point, the lines containing the vectors are perpendicular. Hence, if ![]() and
and ![]() are orthogonal, we write
are orthogonal, we write ![]()
Note there is no `zero product property’ for the dot product. As with the vectors in number 2 above, it is quite possible to have ![]() but neither
but neither ![]() nor
nor ![]() be
be ![]()
Finally, if ![]() , then
, then ![]() so
so ![]() is an acute angle, as in the case of number 3 above.
is an acute angle, as in the case of number 3 above.
We summarize all of our observations in the schematic below.
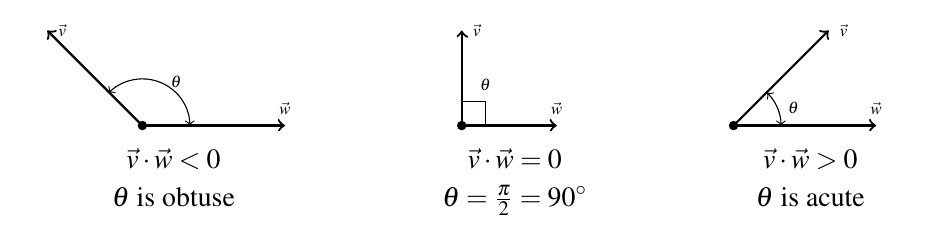
Of the three cases diagrammed above, the one which has the most mathematical significance moving forward is the orthogonal case. Hence, we state the corresponding theorem below.
Basically, Theorem 9.8 tells us that `the dot product detects orthogonality.’ This is a helpful interpretation to keep in mind as you continue your study of vectors in later courses.
We have already argued one direction of Theorem 9.8, namely if ![]() then
then ![]() in the comments following Example 9.2.2.
in the comments following Example 9.2.2.
To show the converse, we note if ![]() , then the angle between
, then the angle between ![]() and
and ![]() ,
, ![]() . From Theorem 9.6, we have that
. From Theorem 9.6, we have that ![]() , as required.
, as required.
We can use Theorem 9.8 in the following example to provide a different proof about the relationship between the slopes of perpendicular lines.[2]
Example 9.2.3
Example 9.2.3
Let ![]() be the line
be the line ![]() and let
and let ![]() be the line
be the line ![]() . Prove that
. Prove that ![]() is perpendicular to
is perpendicular to ![]() if and only if
if and only if ![]() .
.
Solution:
Our strategy is to find two vectors: ![]() , which has the same direction as
, which has the same direction as ![]() , and
, and ![]() , which has the same direction as
, which has the same direction as ![]() and show
and show ![]() if and only if
if and only if ![]()
To that end, we substitute ![]() and
and ![]() into
into ![]() to find two points which lie on
to find two points which lie on ![]() , namely
, namely ![]() and
and ![]() .
.
We let ![]() . Because
. Because ![]() is determined by two points on
is determined by two points on ![]() , it may be viewed as lying on
, it may be viewed as lying on ![]() , so
, so ![]() has the same direction as
has the same direction as ![]()
Similarly, we get the vector ![]() which has the same direction as the line
which has the same direction as the line ![]() . Hence,
. Hence, ![]() and
and ![]() are perpendicular if and only if
are perpendicular if and only if ![]() . According to Theorem 9.8,
. According to Theorem 9.8, ![]() if and only if
if and only if ![]()
Notice that ![]() . Hence,
. Hence, ![]() if and only if
if and only if ![]() , which is true if and only if
, which is true if and only if ![]() , as required.
, as required.
9.2.1 Vector Projections
While Theorem 9.8 certainly gives us some insight into what the dot product means geometrically, there is more to the story of the dot product. Consider the two nonzero vectors ![]() and
and ![]() drawn with a common initial point
drawn with a common initial point ![]() below. For the moment, assume that the angle between
below. For the moment, assume that the angle between ![]() and
and ![]() ,
, ![]() , is acute.
, is acute.
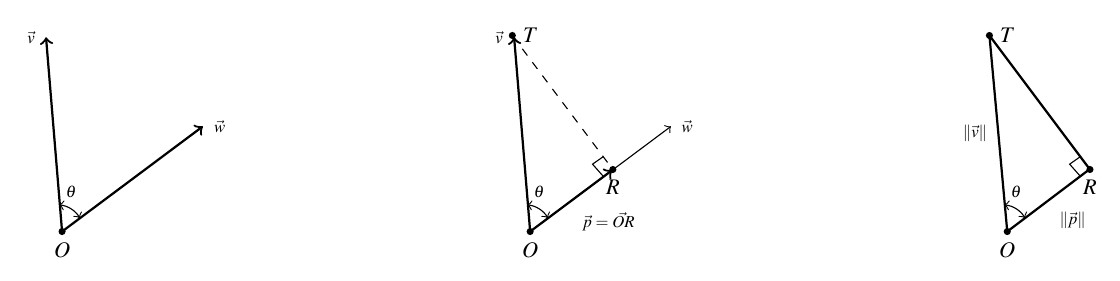
We wish to develop a formula for the vector ![]() , indicated below, which is called the orthogonal projection of
, indicated below, which is called the orthogonal projection of ![]() onto
onto ![]() The vector
The vector ![]() is obtained geometrically as follows: drop a perpendicular from the terminal point
is obtained geometrically as follows: drop a perpendicular from the terminal point ![]() of
of ![]() to the vector
to the vector ![]() and call the point of intersection
and call the point of intersection ![]() . The vector
. The vector ![]() is then defined as
is then defined as ![]()
Like any vector, ![]() is determined by its magnitude
is determined by its magnitude ![]() and its direction
and its direction ![]() according to the formula
according to the formula ![]() . Because we want
. Because we want ![]() to have the same direction as
to have the same direction as ![]() , we have
, we have ![]()
To determine ![]() , we apply Definition 7.2 to the right triangle
, we apply Definition 7.2 to the right triangle ![]() . We find
. We find ![]() , or, equivalently,
, or, equivalently, ![]() . Using Theorems 9.6 and 9.5, we get:
. Using Theorems 9.6 and 9.5, we get:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \| \vec{p} \| &=& \| \vec{v} \| \cos(\theta)\\[4pt] &=& \frac{ \| \vec{v} \| \| \vec{w} \| \cos(\theta)}{\| \vec{w} \|}\\[8pt] &=& \frac{\vec{v} \cdot \vec{w}}{\|\vec{w}\|}\\[8pt] &=& \vec{v} \cdot \left(\frac{1}{\|\vec{w}\|} \vec{w}\right)\\[10pt] &=& \vec{v} \cdot \bm\hat{w} \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4921172837aa89ce9e9c2969c702aec0_l3.png)
Hence, ![]() , and as
, and as ![]() , we have
, we have
![]()
Now suppose that the angle ![]() between
between ![]() and
and ![]() is obtuse, and consider the diagram below.
is obtuse, and consider the diagram below.
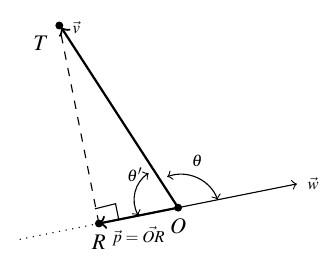
In this case, we see that ![]() and using the triangle
and using the triangle ![]() , we find
, we find ![]() . Because
. Because ![]() , it follows that
, it follows that ![]() , which means
, which means
![]()
Rewriting this last equation in terms of ![]() and
and ![]() as before, we get
as before, we get ![]() . Putting this together with
. Putting this together with ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{p} &=& \| \vec{p} \| \bm\hat{p}\\ &=& -(\vec{v} \cdot \bm\hat{w}) (-\bm\hat{w}) \\ &=& (\vec{v} \cdot \bm\hat{w}) \bm\hat{w} \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7ec4414df8faf38af87e5b6080feb05e_l3.png)
in this case as well.
If the angle between ![]() and
and ![]() is
is ![]() then it is easy to show[3] that
then it is easy to show[3] that ![]() . Because
. Because ![]() in this case,
in this case, ![]() . It follows that
. It follows that ![]() and
and ![]() in this case, too. We have motivated the following.
in this case, too. We have motivated the following.
Definition 9.8
Let ![]() and
and ![]() be nonzero vectors.
be nonzero vectors.
The orthogonal projection of ![]() onto
onto ![]() denoted
denoted ![]() is given by
is given by ![]()
Definition 9.8 gives us a good idea what the dot product does. The scalar ![]() is a measure of how much of the vector
is a measure of how much of the vector ![]() is in the direction of the vector
is in the direction of the vector ![]() and is thus called the scalar projection of
and is thus called the scalar projection of ![]() onto
onto ![]()
While the formula given in Definition 9.8 is theoretically appealing, because of the presence of the normalized unit vector ![]() , computing the projection using the formula
, computing the projection using the formula ![]() can be messy. We present two other formulas that are often used in practice.
can be messy. We present two other formulas that are often used in practice.
The proof of Theorem 9.9, which we leave to the reader as an exercise, amounts to using the formula ![]() and properties of the dot product. It is time for an example.
and properties of the dot product. It is time for an example.
Example 9.2.4
Example 9.2.4
Let ![]() and
and ![]() . Determine
. Determine ![]() . Check your answer geometrically.
. Check your answer geometrically.
Solution:
We find
![]()
and
![]()
Hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{p} &=& \frac{\vec{v} \cdot \vec{w}}{\vec{w} \cdot \vec{w}} \vec{w} \\[10pt] &=& \frac{15}{5} \left<-1,2\right>\\[10pt] &=& \left<-3,6\right> \end{array}\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-86742669b5b5178674476480f42e2811_l3.png)
We plot ![]() ,
, ![]() and
and ![]() in standard position below on the left. We see
in standard position below on the left. We see ![]() has the same direction as
has the same direction as ![]() , but we need to do more to show
, but we need to do more to show ![]() in is indeed the orthogonal projection of
in is indeed the orthogonal projection of ![]() onto
onto ![]() .
.
Consider the vector ![]() whose initial point is the terminal point of
whose initial point is the terminal point of ![]() and whose terminal point is the terminal point of
and whose terminal point is the terminal point of ![]() . From the definition of vector arithmetic,
. From the definition of vector arithmetic, ![]() , so that
, so that ![]() .
.
For ![]() and
and ![]() , then
, then ![]()
To prove ![]() , we compute the dot product:
, we compute the dot product:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{q} \cdot \vec{w} &=& \left<4,2\right> \cdot \left<-1,2\right> \\ &=& (-4)+4 \\ &=& 0 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a21f0fae93505e5022e6364959e62965_l3.png)
Hence, per Theorem 9.8, we know ![]() which completes our check.[4]
which completes our check.[4]
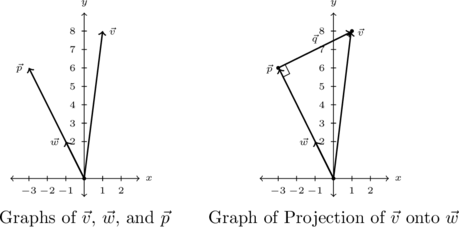
In Example 9.2.4 above, writing ![]() is an example of what is called a vector decomposition of
is an example of what is called a vector decomposition of ![]() . We generalize this result in the following theorem.
. We generalize this result in the following theorem.
Theorem 9.10 Generalized Decomposition Theorem
Let ![]() and
and ![]() be nonzero vectors. There are unique vectors
be nonzero vectors. There are unique vectors ![]() and
and ![]() such that
such that ![]() where
where ![]() for some scalar
for some scalar ![]() , and
, and ![]()
If the vectors ![]() and
and ![]() in Theorem 9.10 are nonzero, then we can say
in Theorem 9.10 are nonzero, then we can say ![]() is `parallel’[5] to
is `parallel’[5] to ![]() and
and ![]() is `orthogonal’ to
is `orthogonal’ to ![]() . In this case, the vector
. In this case, the vector ![]() is sometimes called the `vector component of
is sometimes called the `vector component of ![]() parallel to
parallel to ![]() ‘ and
‘ and ![]() is called the `vector component of
is called the `vector component of ![]() orthogonal to
orthogonal to ![]() .’
.’
To prove Theorem 9.10, we take ![]() and
and ![]() . Then
. Then ![]() is, by definition, a scalar multiple of
is, by definition, a scalar multiple of ![]() . Next, we compute
. Next, we compute ![]()
![Rendered by QuickLaTeX.com \[ \begin{array}{rcll} \vec{q} \cdot \vec{w} & = & (\vec{v} - \vec{p}) \cdot \vec{w}& \text{Definition of } \vec{q} \\ [3pt] & = & \vec{v} \cdot \vec{w} - \vec{p} \cdot \vec{w} & \text{Properties of Dot Product} \\ [8pt] & = & \vec{v} \cdot \vec{w} - \left(\dfrac{\vec{v} \cdot \vec{w}}{\vec{w} \cdot \vec{w}} \vec{w}\right) \cdot \vec{w} & \vec{p} = \text{proj}_{\vec{w}}(\vec{v}) \\ [8pt] & = & \vec{v} \cdot \vec{w} - \left(\dfrac{\vec{v} \cdot \vec{w}}{\vec{w} \cdot \vec{w}}\right) (\vec{w} \cdot \vec{w}) & \text{Properties of Dot Product} \\ [8pt] & = & \vec{v} \cdot \vec{w} - \vec{v}\cdot \vec{w} & \\ [3pt] & = & 0 & \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-bdfc04fc4aaccab83927ed12a07f8230_l3.png)
Hence, ![]() , as required. At this point, we have shown that the vectors
, as required. At this point, we have shown that the vectors ![]() and
and ![]() guaranteed by Theorem 9.10 exist. Now we need to show that they are unique – that is, there is only one such way to decompose
guaranteed by Theorem 9.10 exist. Now we need to show that they are unique – that is, there is only one such way to decompose ![]() in the manner described in Theorem 9.10.
in the manner described in Theorem 9.10.
Suppose ![]() where the vectors
where the vectors ![]() and
and ![]() satisfy the same properties described in Theorem 9.10 as
satisfy the same properties described in Theorem 9.10 as ![]() and
and ![]() . Then
. Then ![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{w} \cdot (\vec{p} - \vec{p} \,') & =& \vec{w} \cdot (\vec{q} \,' - \vec{q}) \\ &=& \vec{w} \cdot \vec{q} \,' - \vec{w} \cdot \vec{q} \\ &=& 0 - 0 \\ &=& 0 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-62a20571ef983a01df373a1d24a56249_l3.png)
The long and short of this computation is that ![]()
Now there are scalars ![]() and
and ![]() so that
so that ![]() and
and ![]() . This means
. This means
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{w} \cdot (\vec{p} - \vec{p} \,') &=& \vec{w} \cdot ( k \vec{w} - k \,' \vec{w}) \\ &=& \vec{w} \cdot ([k - k \,'] \vec{w}) \\ &=& (k - k \,') (\vec{w} \cdot \vec{w}) \\ &=& (k - k \,') \| \vec{w} \|^2 \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f01865f7f6caf2fed7471c4027978e37_l3.png)
Because ![]() ,
, ![]() , which means the only way
, which means the only way ![]() is for
is for ![]() , or
, or ![]() . \vskip 0.5em
. \vskip 0.5em
This means ![]() . As
. As ![]() , it must be that
, it must be that ![]() as well.
as well.
Hence, we have shown there is only one way to write ![]() as a sum of vectors as described in Theorem 9.10, so the decomposition listed there is unique.
as a sum of vectors as described in Theorem 9.10, so the decomposition listed there is unique.
We close this section with an application of the dot product. In Physics, if a constant force ![]() is exerted over a distance
is exerted over a distance ![]() , the work
, the work ![]() done by the force is given by
done by the force is given by ![]() . Here, the assumption is that the force is being applied in the direction of the motion. If the force applied is not in the direction of the motion, we can use the dot product to find the work done.
. Here, the assumption is that the force is being applied in the direction of the motion. If the force applied is not in the direction of the motion, we can use the dot product to find the work done.
Consider the scenario sketched below in which the constant force ![]() is applied to move an object from the point
is applied to move an object from the point ![]() to the point
to the point ![]() . Here the force is being applied at an angle
. Here the force is being applied at an angle ![]() as opposed to being applied directly in the direction of the motion.
as opposed to being applied directly in the direction of the motion.
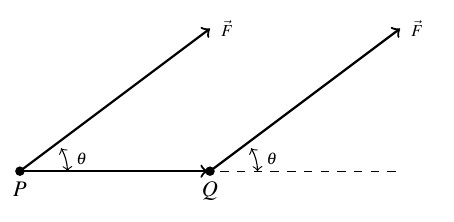
To find the work ![]() done in this scenario, we need to find how much of the force
done in this scenario, we need to find how much of the force ![]() is in the direction of the motion
is in the direction of the motion ![]() . This is precisely what the dot product
. This is precisely what the dot product ![]() represents.
represents.
The distance the object travels is ![]() , so we get
, so we get ![]() . As
. As ![]() , we can simplify this formula as follows:
, we can simplify this formula as follows: ![]()
Using Theorem 9.6, we can rewrite ![]() , where
, where ![]() is the angle between the applied force
is the angle between the applied force ![]() and the trajectory of the motion
and the trajectory of the motion ![]() . We have proved the following.
. We have proved the following.
Theorem 9.11 Work as a Dot Product
Suppose a constant force ![]() is applied along the vector
is applied along the vector ![]() . The work
. The work ![]() done by
done by ![]() is given by
is given by
![]()
where ![]() is the angle between
is the angle between ![]() and
and ![]()
We test out our formula for work in the following example.
Example 9.2.5
Example 9.2.5
Taylor exerts a force of ![]() pounds to pull her wagon a distance of
pounds to pull her wagon a distance of ![]() feet over level ground. If the handle of the wagon makes a
feet over level ground. If the handle of the wagon makes a ![]() angle with the horizontal, how much work did Taylor do pulling the wagon? Assume the force of
angle with the horizontal, how much work did Taylor do pulling the wagon? Assume the force of ![]() pounds is exerted at a
pounds is exerted at a ![]() angle for the duration of the
angle for the duration of the ![]() feet.
feet.
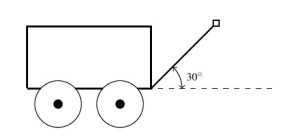
Solution:
There are (at least) two ways to attack this problem. One way is to find the vectors ![]() and
and ![]() mentioned in Theorem 9.11 and compute
mentioned in Theorem 9.11 and compute ![]() .
.
To do this, we assume the origin is at the point where the handle of the wagon meets the wagon and the positive ![]() -axis lies along the dashed line in the figure above.
-axis lies along the dashed line in the figure above.
To find the force vector ![]() , we note the force in this situation is a constant 10 pounds, so
, we note the force in this situation is a constant 10 pounds, so ![]() . Moreover, the force is being applied at a constant angle of
. Moreover, the force is being applied at a constant angle of ![]() with respect to the positive
with respect to the positive ![]() -axis. Definition 9.4 gives us
-axis. Definition 9.4 gives us
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \vec{F} &=& \| \vec{F} \| \left< \cos(\theta), \sin(\theta) \right>\\ &=& 10 \left<\cos(30^{\circ}), \sin(30^{\circ})\right>\\ &=& \left<5\sqrt{3}, 5\right> \end{array} \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fafbb3c9dbdcc5dde273fbbdd32172e3_l3.png)
The wagon is being pulled along 50 feet in the positive ![]() -direction, so we find the displacement vector is
-direction, so we find the displacement vector is
![]()
Per Theorem 9.11, ![]() .
.
Force is measured in pounds and distance is measured in feet, giving us ![]() foot-pounds.
foot-pounds.
Alternatively, we can use the formula ![]() . With
. With ![]() pounds,
pounds, ![]() feet and
feet and ![]() , we get
, we get ![]() foot-pounds of work.
foot-pounds of work.
9.2.2 Section Exercises
In Exercises 1 – 20, use the pair of vectors ![]() and
and ![]() to find the following quantities.
to find the following quantities.
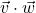
- The angle
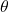 (in degrees) between
(in degrees) between 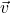 and
and 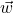
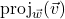
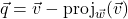 (Show that
(Show that 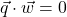 .)
.)
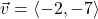 and
and 
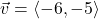 and
and 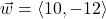
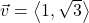 and
and 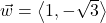
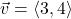 and
and 
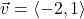 and
and 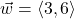
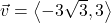 and
and 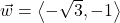
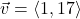 and
and 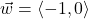
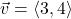 and
and 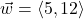
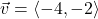 and
and 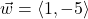
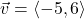 and
and 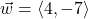
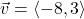 and
and 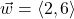
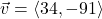 and
and 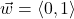
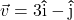 and
and 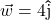
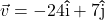 and
and 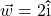
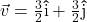 and
and 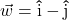
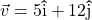 and
and 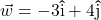
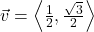 and
and 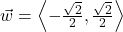
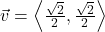 and
and 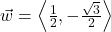
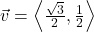 and
and 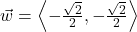
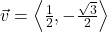 and
and 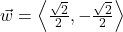
- A force of
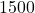 pounds is required to tow a trailer. Find the work done towing the trailer along a flat stretch of road
pounds is required to tow a trailer. Find the work done towing the trailer along a flat stretch of road 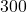 feet. Assume the force is applied in the direction of the motion.
feet. Assume the force is applied in the direction of the motion. - Find the work done lifting a
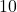 pound book
pound book 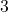 feet straight up into the air. Assume the force of gravity is acting straight downwards.
feet straight up into the air. Assume the force of gravity is acting straight downwards. - Suppose Taylor fills her wagon with rocks and must exert a force of 13 pounds to pull her wagon across the yard. If she maintains a
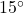 angle between the handle of the wagon and the horizontal, compute how much work Taylor does pulling her wagon 25 feet. Round your answer to two decimal places.
angle between the handle of the wagon and the horizontal, compute how much work Taylor does pulling her wagon 25 feet. Round your answer to two decimal places. - In Exercise 61 in Section 9.1, two drunken college students have filled an empty beer keg with rocks which they drag down the street by pulling on two attached ropes. The stronger of the two students pulls with a force of 100 pounds on a rope which makes a
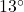 angle with the direction of motion. (In this case, the keg was being pulled due east and the student’s heading was N
angle with the direction of motion. (In this case, the keg was being pulled due east and the student’s heading was N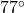 E.) Find the work done by this student if the keg is dragged 42 feet.
E.) Find the work done by this student if the keg is dragged 42 feet. - Find the work done pushing a 200 pound barrel 10 feet up a
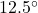 incline. Ignore all forces acting on the barrel except gravity, which acts downwards. Round your answer to two decimal places.
incline. Ignore all forces acting on the barrel except gravity, which acts downwards. Round your answer to two decimal places.
HINT: Because you are working to overcome gravity only, the force being applied acts directly upwards. This means that the angle between the applied force in this case and the motion of the object is not the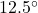 of the incline!
of the incline! - Prove the distributive property of the dot product in Theorem 9.5.
- Finish the proof of the scalar property of the dot product in Theorem 9.5.
- Show Theorem 9.10 reduces to Theorem 9.4 in the case
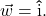
- Use the identity in Example 9.2.1 to prove the Parallelogram Law
![Rendered by QuickLaTeX.com \[ \|\vec{v}\|^2 + \|\vec{w}\|^2 = \dfrac{1}{2}\left[ \| \vec{v} + \vec{w}\|^2 + \|\vec{v} - \vec{w}\|^2\right] \]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-58e05a41b0a11500c41aff15e0c84ca8_l3.png)
- We know that
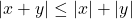 for all real numbers
for all real numbers 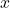 and
and 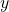 by the Triangle Inequality established in Exercise 55 in Section 1.4. We can now establish a Triangle Inequality for vectors. In this exercise, we prove that
by the Triangle Inequality established in Exercise 55 in Section 1.4. We can now establish a Triangle Inequality for vectors. In this exercise, we prove that 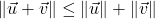 for all pairs of vectors
for all pairs of vectors 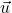 and
and 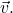
- (Step 1) Show that
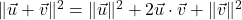 .
. - (Step 2) Show that
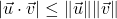 . This is the celebrated Cauchy-Schwarz Inequality.[6]
. This is the celebrated Cauchy-Schwarz Inequality.[6]
HINT: Start with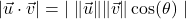 and use the fact that
and use the fact that 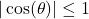 for all
for all 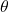 .
. - (Step 3) Show:
![Rendered by QuickLaTeX.com \[\| \vec{u} + \vec{v} \|^{2} = \| \vec{u} \|^{2} + 2\vec{u} \cdot \vec{v} + \| \vec{v} \|^{2} \leq \| \vec{u} \|^{2} + 2|\vec{u} \cdot \vec{v}| + \| \vec{v} \|^{2} \leq \| \vec{u} \|^{2} + 2\| \vec{u} \| \| \vec{v} \| + \| \vec{v} \|^{2} = (\| \vec{u} \| + \| \vec{v} \|)^{2}.\]](https://odp.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9b4fc427505a3ddcd87ff91a5c26911a_l3.png)
- (Step 4) Use Step 3 to show that
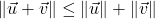 for all pairs of vectors
for all pairs of vectors 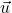 and
and 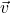 .
.
- (Step 1) Show that
Section 9.2 Exercise Answers can be found in the Appendix … Coming soon
The product of two vectors

