"

Section 2.1 Answers

  1. [latex]f(x) = x^{2} + 2[/latex] (this is both forms!)
    • No [latex]x[/latex]-intercepts
    • [latex]y[/latex]-intercept [latex](0, 2)[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Range: [latex][2, \infty)[/latex]
    • Decreasing on [latex](-\infty, 0][/latex]
    • Increasing on [latex][0, \infty)[/latex]
    • Vertex [latex](0, 2)[/latex] is a minimum
    • Axis of symmetry [latex]x = 0[/latex]
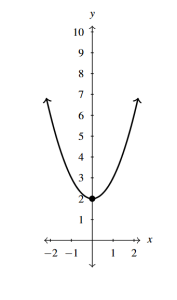
    • The rectangular plane with a parabola that opens up and has a vertex of (0,2).
      Answer to Exercise 1
  2. [latex]f(x) = -(x + 2)^{2} = -x^2-4x-4[/latex]
    • [latex]x[/latex]-intercept [latex](-2, 0)[/latex]
    • [latex]y[/latex]-intercept [latex](0, -4)[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Range: [latex](-\infty, 0][/latex]
    • Increasing on [latex](-\infty, -2][/latex]
    • Decreasing on [latex][-2, \infty)[/latex]
    • Vertex [latex](-2, 0)[/latex] is a maximum
    • Axis of symmetry [latex]x = -2[/latex]
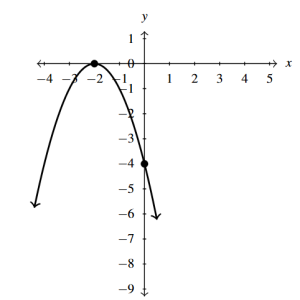
    • The rectangular plane with a parabola that opens down and has a vertex of (-2,0).
      Answer to Exercise 2
  3. [latex]f(x) = x^{2} - 2x - 8 = (x - 1)^{2} - 9[/latex]
    • [latex]x[/latex]-intercepts [latex](-2, 0)[/latex] and [latex](4, 0)[/latex]
    • [latex]y[/latex]-intercept [latex](0, -8)[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Range: [latex][-9, \infty)[/latex]
    • Decreasing on [latex](-\infty, 1][/latex]
    • Increasing on [latex][1, \infty)[/latex]
    • Vertex [latex](1, -9)[/latex] is a minimum
    • Axis of symmetry [latex]x = 1[/latex]
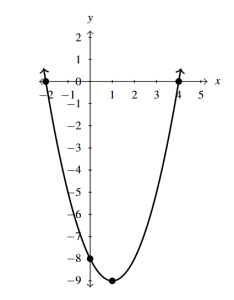
    • The rectangular plane with a parabola that opens up and has a vertex of (1,-9).
      Answer to Exercise 3
  4. [latex]g(t) = -2(t + 1)^{2} + 4 = -2t^2-4t+2[/latex]
    • [latex]t[/latex]-intercepts [latex](-1 - \sqrt{2}, 0)[/latex] and [latex](-1 + \sqrt{2}, 0)[/latex]
    • [latex]y[/latex]-intercept [latex](0, 2)[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Range: [latex](-\infty, 4][/latex]
    • Increasing on [latex](-\infty, -1][/latex]
    • Decreasing on [latex][-1, \infty)[/latex]
    • Vertex [latex](-1, 4)[/latex] is a maximum
    • Axis of symmetry [latex]t = -1[/latex]
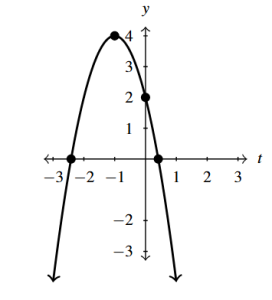
    • The rectangular plane with a parabola that opens down and has a vertex of (-1,4).
      Answer to Exercise 4
  5. [latex]g(t) = 2t^2-tx-1 = 2(t-1)^2-3[/latex]
    • [latex]t[/latex]-intercepts [latex]\left(\frac{2-\sqrt{6}}{2}, 0\right)[/latex] and [latex]\left(\frac{2+\sqrt{6}}{2}, 0\right)[/latex]
    • [latex]y[/latex]-intercept [latex](0, -1)[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Range: [latex][-3, \infty)[/latex]
    • Increasing on [latex][1,\infty)[/latex]
    • Decreasing on [latex](-\infty,1][/latex]
    • Vertex [latex](1, -3)[/latex] is a minimum
    • Axis of symmetry [latex]t = 1[/latex]
    • The rectangular plane with a parabola that opens up and has a vertex of (1,-3).
      Answer to Exercise 5
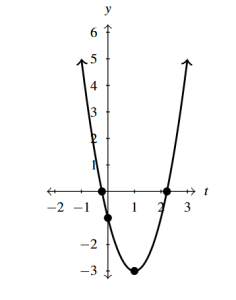
  6. [latex]g(t) = -3t^{2} + 4t - 7 = -3\left(t - \frac{2}{3} \right)^{2} - \frac{17}{3}[/latex]
    • No [latex]t[/latex]-intercepts
    • [latex]y[/latex]-intercept [latex](0, -7)[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Range: [latex]\left(-\infty, -\frac{17}{3}\right][/latex]
    • Increasing on [latex]\left(-\infty, \frac{2}{3}\right][/latex]
    • Decreasing on [latex]\left[\frac{2}{3}, \infty\right)[/latex]
    • Vertex [latex]\left(\frac{2}{3}, -\frac{17}{3}\right)[/latex] is a maximum
    • Axis of symmetry [latex]t = \frac{2}{3}[/latex]
    • The rectangular plane with a parabola that opens down and has a y-intercept of (0,-4).
      Answer to Exercise 6
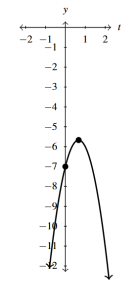
  7. [latex]h(s) = s^2+s+1 = \left(s + \frac{1}{2}\right)^{2} + \frac{3}{4}[/latex]
    • No [latex]s[/latex]-intercepts
    • [latex]y[/latex]-intercept [latex](0, 1)[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Range: [latex]\left[ \frac{3}{4}, \infty\right)[/latex]
    • Increasing on [latex]\left[-\frac{1}{2}, \infty\right)[/latex]
    • Decreasing on [latex]\left(-\infty, -\frac{1}{2}\right][/latex]
    • Vertex [latex]\left(-\frac{1}{2}, \frac{3}{4}\right)[/latex] is a minimum
    • Axis of symmetry [latex]s = -\frac{1}{2}[/latex]
    • The rectangular plane with a parabola that opens up and has a y-intercept of (0,1).
      Answer to Exercise 7
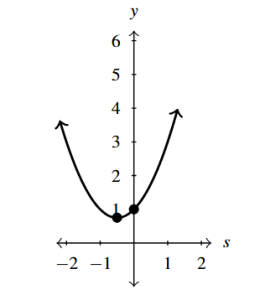
  8. [latex]h(s) = -3s^2+5s+4 = -3\left(s-\frac{5}{6}\right)^2 + \frac{73}{12}[/latex]
    • [latex]s[/latex]-intercepts [latex]\left(\frac{5 - \sqrt{73}}{6}, 0\right)[/latex] and [latex]\left(\frac{5+\sqrt{73}}{6}, 0\right)[/latex]
    • [latex]y[/latex]-intercept [latex](0, 4)[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Range: [latex]\left(-\infty, \frac{73}{12} \right][/latex]
    • Increasing on [latex]\left(-\infty, \frac{5}{6}\right][/latex]
    • Decreasing on [latex]\left[ \frac{5}{6}, \infty\right)[/latex]
    • Vertex [latex]\left(\frac{5}{6}, \frac{73}{12} \right)[/latex] is a maximum
    • Axis of symmetry [latex]s = \frac{5}{6}[/latex]
    • The rectangular plane with a parabola that opens down and has a y-intercept of (0,4).
      Answer to Exercise 8
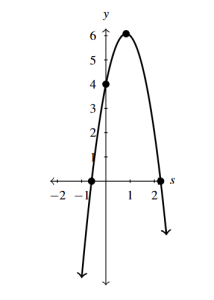
  9. [latex]h(s) = s^{2} - \frac{1}{100} s - 1 = \left(s - \frac{1}{200}\right)^{2} - \frac{40001}{40000}[/latex]
    • [latex]s[/latex]-intercepts [latex]\left(\frac{1 + \sqrt{40001}}{200}\right)[/latex] and [latex]\left(\frac{1 - \sqrt{40001}}{200}\right)[/latex]
    • [latex]y[/latex]-intercept [latex](0, -1)[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Range: [latex]\left[-\frac{40001}{40000}, \infty \right)[/latex]
    • Decreasing on [latex]\left(-\infty, \frac{1}{200}\right][/latex]
    • Increasing on [latex]\left[\frac{1}{200}, \infty \right)[/latex]
    • Vertex [latex]\left(\frac{1}{200}, -\frac{40001}{40000}\right)[/latex] is a minimum[1]
    • Axis of symmetry [latex]s = \frac{1}{200}[/latex]
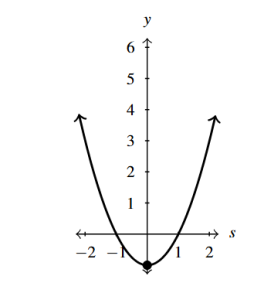
    • The rectangular plane with a parabola that opens up and has a vertex of (0,1).
      Answer to Exercise 9
  10. [latex]F(x) = (x+2)^2-3[/latex]
  11. [latex]F(x) = \frac{1}{2}(x-2)^2-1[/latex]
  12. [latex]F(x) = -x^2+4[/latex]
  13. [latex]F(x) =-2(x-1.5)^2+4.5[/latex]
  14. [latex]P(x) = -2x^2+28x-26[/latex], for [latex]0 \leq x \leq 15[/latex]
    • 7 T-shirts should be made and  sold to maximize profit.
    • The maximum profit is $72.
    • The price per T-shirt should be set at $16 to maximize profit.
    • The break even points are [latex]x=1[/latex] and [latex]x=13[/latex], so to make a profit, between 1 and 13 T-shirts need to be made and sold.
  15. [latex]P(x) = -x^2+25x-100[/latex], for [latex]0 \leq x \leq 35[/latex]
    • because the vertex occurs at [latex]x=12.5[/latex], and it is impossible to make or sell 12.5 bottles of tonic, maximum profit occurs when either 12 or 13 bottles of tonic are made and sold.
    • The maximum profit is $56.
    • The price per bottle can be either $23 (to sell 12 bottles) or $22 (to sell 13 bottles.) Both will result in the maximum profit.
    • The break even points are [latex]x=5[/latex] and [latex]x=20[/latex], so to make a profit, between 5 and 20 bottles of tonic need to be made and sold.
  16. [latex]P(x) = -3x^2+72x-240[/latex], for [latex]0 \leq x \leq 30[/latex]
    • 12 cups of lemonade need to be made and sold to maximize profit.
    • The maximum profit is 192 cents or $1.92.
    • The price per cup should be set at 54 cents per cup to maximize profit.
    • The break even points are [latex]x=4[/latex] and [latex]x=20[/latex], so to make a profit, between 4 and 20 cups of lemonade need to be made and sold.
  17. [latex]P(x) = -0.5 x^2+9x-36[/latex], for [latex]0 \leq x \leq 24[/latex]
    • 9 pies should be made and sold to maximize the daily profit.
    • The maximum daily profit is $4.50.
    • The price per pie should be set at $7.50 to maximize profit.
    • The break even points are [latex]x=6[/latex] and [latex]x=12[/latex], so to make a profit, between 6 and 12 pies need to be made and sold daily.
  18. [latex]P(x) = -2x^2+120x-1000[/latex], for [latex]0 \leq x \leq 70[/latex]
    • 30 scooters need to be made and sold to maximize profit.
    • The maximum monthly profit is 800 hundred dollars, or $80,000.
    • The price per scooter should be set at 80 hundred dollars, or $8000per scooter.
    • The break even points are [latex]x=10[/latex] and [latex]x=50[/latex], so to make a profit, between 10 and 50 scooters need to be made and sold monthly
  19. 495 cookies
  20. The vertex is (approximately) [latex](29.60, 22.66)[/latex], which corresponds to a maximum fuel economy of 22.66 miles per gallon, reached sometime between 2009 and 2010 (29 — 30 years after 1980.) Unfortunately, the model is only valid up until 2008 (28 years after 1908.) So, at this point, we are using the model to predict the maximum fuel economy.
  21. [latex]64^{\circ}[/latex] at 2 PM (8 hours after 6 AM.)
  22. 5000 pens should be produced for a cost of $200.
  23. 8 feet by 16 feet; maximum area is 128 square feet.
  24. 50 feet by 50 feet; maximum area is 2500 feet; he can raise 100 average alpacas.
  25. The largest rectangle has area [latex]12.25[/latex] square inches.
  26. Make the vertex of the parabola [latex](0, 10)[/latex] so that the point on the top of the left-hand tower where the cable connects is [latex](-200, 100)[/latex] and the point on the top of the right-hand tower is [latex](200, 100)[/latex]. Then the parabola is given by [latex]p(x) = \frac{9}{4000}x^{2} + 10[/latex]. Standing [latex]50[/latex] feet to the right of the left-hand tower means you’re standing at [latex]x= -150[/latex] and [latex]p(-150) = 60.625[/latex]. So the cable is 60.625 feet above the bridge deck there.
  27. [latex]x = \pm y\sqrt{10}[/latex]
  28. [latex]x = \pm (y - 2)[/latex]
  29. [latex]x = \dfrac{m \pm \sqrt{m^{2} + 4}}{2}[/latex]
  30. [latex]y = \dfrac{3 \pm \sqrt{16x + 9}}{2}[/latex]
  31. [latex]y = 2 \pm x[/latex]
  32. [latex]t = \dfrac{v_{0} \pm \sqrt{v_{0}^{2} + 4gs_{0}}}{2g}[/latex]
  33. .
    1. i. [latex]L(x) = x^2[/latex], ii. [latex]L(x) = 2x^2+x[/latex], iii. [latex]L(x) = -x^2+5x+1[/latex]
    2. Answer May Vary
    3. The three points lie on the same line and we get [latex]L(x) = -x+5[/latex].
    4. To obtain a quadratic function, we require that the points are not collinear (i.e., they do not all lie on the same line.)

Section 2.2 Answers

  1. [latex]F(x) = (x + 2)^{3} + 1[/latex]
    • domain: [latex](-\infty, \infty)[/latex]
    • range: [latex](-\infty, \infty)[/latex]
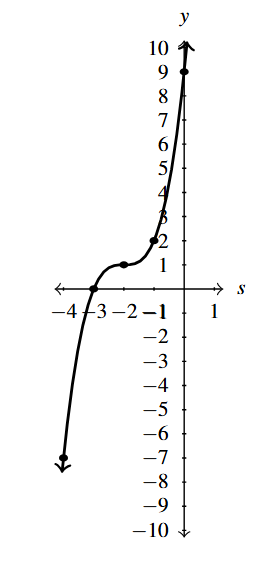
    • The rectangular plane with an odd degree polynomial that increases left to right.
      Answer to Exercise 1
  2. [latex]F(x) = (x + 2)^{4} + 1[/latex]
    • domain: [latex](-\infty, \infty)[/latex]
    • range: [latex][1, \infty)[/latex]
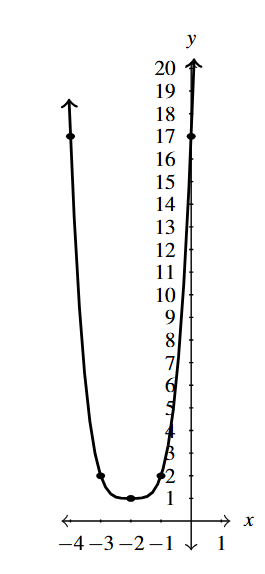
    • The rectangular plane with an even degree polynomial.
      Answer to Exercise 2
  3. [latex]F(x) = 2 - 3(x - 1)^{4}[/latex]
    • domain: [latex](-\infty, \infty)[/latex]
    • range: [latex](-\infty, 2][/latex]
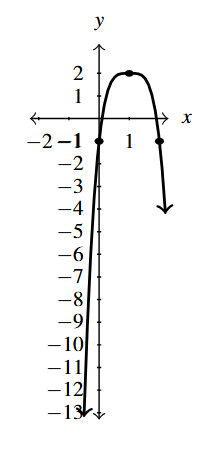
    • The rectangular plane with an even degree polynomial that opens down.
      Answer to Exercise 3
  4. [latex]F(x) = -x^{5} - 3[/latex]
    • domain: [latex](-\infty, \infty)[/latex]
    • range: [latex](-\infty, \infty)[/latex]
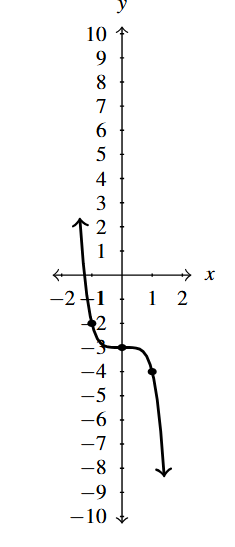
    • The rectangular plane with an odd degree polynomial that decreases left to right.
      Answer to Exercise 4
  5. [latex]F(x) = (x+1)^5+10[/latex]
    • domain: [latex](-\infty, \infty)[/latex]
    • range: [latex](-\infty, \infty)[/latex]
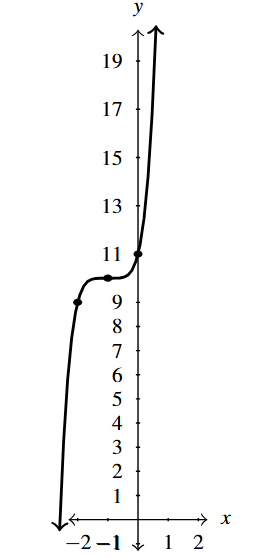
    • The rectangular plane with an odd degree polynomial that increases left to right.
      Answer to Exercise 5
  6. [latex]F(x) = 8-x^{6}[/latex]
    • domain: [latex](-\infty, \infty)[/latex]
    • range: [latex](-\infty, 8][/latex]
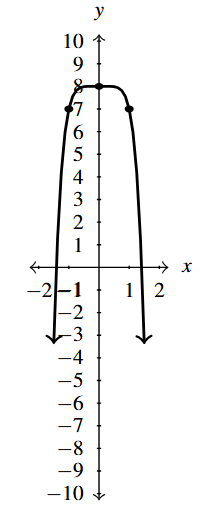
    • The rectangular plane with an even degree polynomial that opens down.
      Answer to Exercise 6
  7. [latex]F(x) = (x-1)^3-2[/latex]
  8. [latex]F(x) = -\frac{1}{2} (x+2)^3+3[/latex]
  9. [latex]F(x) = 2(x+1)^4-4[/latex]
  10. [latex]F(x) = -0.15625x^4+2.5[/latex]
  11. [latex]f(x) = 4-x-3x^2[/latex]
    • Degree 2
    • Leading term [latex]-3x^{2}[/latex]
    • Leading coefficient [latex]-3[/latex]
    • Constant term 4
    • As [latex]x \rightarrow -\infty, \; f(x) \rightarrow -\infty[/latex]
    • As [latex]x \rightarrow \infty, \; f(x) \rightarrow -\infty[/latex]
  12. [latex]g(x) = 3x^5 - 2x^2 + x + 1[/latex]
    • Degree 5
    • Leading term [latex]3x^5[/latex]
    • Leading coefficient 3
    • Constant term 1
    • As [latex]x \rightarrow -\infty, \; g(x) \rightarrow -\infty[/latex]
    • As [latex]x \rightarrow \infty, \; g(x) \rightarrow \infty[/latex]
  13. [latex]q(r) = 1 - 16r^{4}[/latex]
    • Degree 4
    • Leading term [latex]-16r^{4}[/latex]
    • Leading coefficient [latex]-16[/latex]
    • Constant term 1
    • As [latex]r \rightarrow -\infty, \; q(r) \rightarrow -\infty[/latex]
    • As [latex]r \rightarrow \infty, \; q(r) \rightarrow -\infty[/latex]
  14. [latex]Z(b) = 42b - b^{3}[/latex]
    • Degree 3
    • Leading term [latex]-b^{3}[/latex]
    • Leading coefficient [latex]-1[/latex]
    • Constant term 0
    • As [latex]b \rightarrow -\infty, \; Z(b) \rightarrow \infty[/latex]
    • As [latex]b \rightarrow \infty, \; Z(b) \rightarrow -\infty[/latex]
  15. [latex]f(x) = \sqrt{3}x^{17} + 22.5x^{10} - \pi x^{7} + \frac{1}{3}[/latex]
    • Degree 17
    • Leading term [latex]\sqrt{3}x^{17}[/latex]
    • Leading coefficient [latex]\sqrt{3}[/latex]
    • Constant term [latex]\frac{1}{3}[/latex]
    • As [latex]x \rightarrow -\infty, \; f(x) \rightarrow -\infty[/latex]
    • As [latex]x \rightarrow \infty, \; f(x) \rightarrow \infty[/latex]
  16. [latex]s(t) = -4.9t^{2} + v_{0}t + s_{0}[/latex]
    • Degree 2
    • Leading term [latex]-4.9t^{2}[/latex]
    • Leading coefficient [latex]-4.9[/latex]
    • Constant term [latex]s_{0}[/latex]
    • As [latex]t \rightarrow -\infty, \; s(t) \rightarrow -\infty[/latex]
    • As [latex]t \rightarrow \infty, \; s(t) \rightarrow -\infty[/latex]
  17. [latex]P(x) = (x - 1)(x - 2)(x - 3)(x - 4)[/latex]
    • Degree 4
    • Leading term [latex]x^{4}[/latex]
    • Leading coefficient 1
    • Constant term 24
    • As [latex]x \rightarrow -\infty, \; P(x) \rightarrow \infty[/latex]
    • As [latex]x \rightarrow \infty, \; P(x) \rightarrow \infty[/latex]
  18. [latex]p(t) = -t^2(3 - 5t)(t^{2} + t + 4)[/latex]
    • Degree 5
    • Leading term [latex]5t^{5}[/latex]
    • Leading coefficient 5
    • Constant term 0
    • As [latex]t \rightarrow -\infty, \; p(t) \rightarrow -\infty[/latex]
    • As [latex]t \rightarrow \infty, \; p(t) \rightarrow \infty[/latex]
  19. [latex]f(x) = -2x^3(x+1)(x+2)^2[/latex]
    • Degree 6
    • Leading term [latex]-2x^{6}[/latex]
    • Leading coefficient [latex]-2[/latex]
    • Constant term 0
    • As [latex]x \rightarrow -\infty, \; f(x) \rightarrow -\infty[/latex]
    • As [latex]x \rightarrow \infty, \; f(x) \rightarrow -\infty[/latex]
  20. [latex]G(t) = 4(t-2)^2\left(t+\frac{1}{2}\right)[/latex]
    • Degree 3
    • Leading term [latex]4t^3[/latex]
    • Leading coefficient 4
    • Constant term 8
    • As [latex]t \rightarrow -\infty, \; G(t) \rightarrow -\infty[/latex]
    • As [latex]t \rightarrow \infty, \; G(t) \rightarrow \infty[/latex]
  21. [latex]a(x) = x(x + 2)^{2}[/latex]
    • [latex]x = 0[/latex] multiplicity 1
    • [latex]x = -2[/latex] multiplicity 2
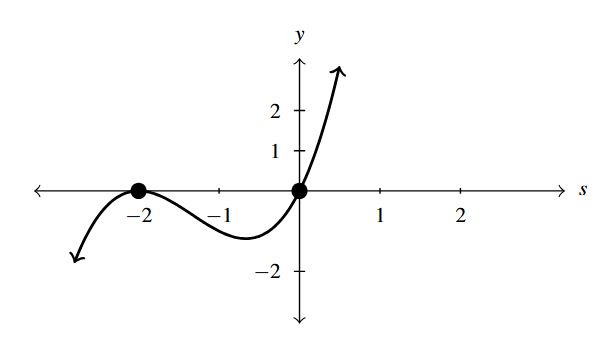
    • The rectangular plane with an odd degree polynomial that increases left to right.
      Answer to Exercise 21
  22. [latex]g(t) = t(t + 2)^{3}[/latex]
    • [latex]t = 0[/latex] multiplicity 1
    • [latex]t = -2[/latex] multiplicity 3
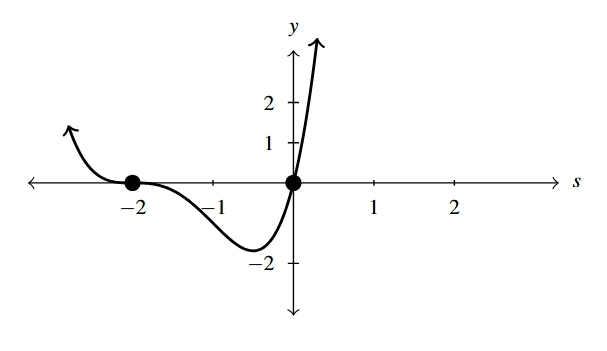
    • The rectangular plane with an even degree polynomial that opens upward.
      Answer to Exercise 22
  23. [latex]f(z) = -2(z-2)^2(z+1)[/latex]
    • [latex]z=2[/latex] multiplicity 2
    • [latex]z=-1[/latex] multiplicity 1
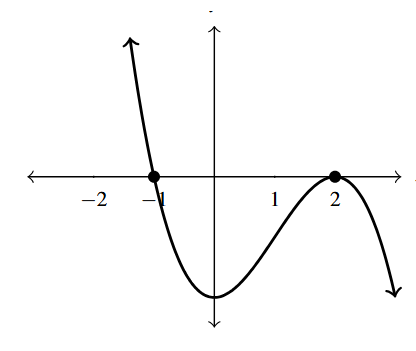
    • The rectangular plane with an odd degree polynomial that mostly decreases left to right.
      Answer to Exercise 23
  24. [latex]g(x) = (2x+1)^2(x-3)[/latex]
    • [latex]x=-\frac{1}{2}[/latex] multiplicity 2
    • [latex]x=3[/latex] multiplicity 1
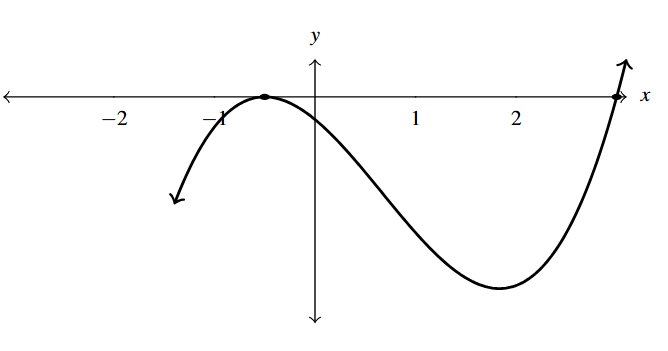
    • The rectangular plane with an odd degree polynomial that mostly increases left to right.
      Answer to Exercise 24
  25. [latex]F(t) = t^{3}(t + 2)^{2}[/latex]
    • [latex]t = 0[/latex] multiplicity 3
    • [latex]t = -2[/latex] multiplicity 2
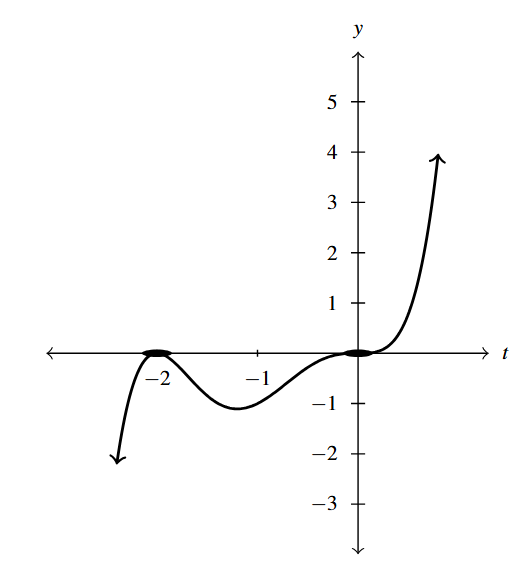
    • The rectangular plane with an odd degree polynomial that most increases left to right.
      Answer to Exercise 25
  26. [latex]P(z) = (z - 1)(z - 2)(z - 3)(z - 4)[/latex]
    • [latex]z = 1[/latex] multiplicity 1
    • [latex]z = 2[/latex] multiplicity 1
    • [latex]z = 3[/latex] multiplicity 1
    • [latex]z = 4[/latex] multiplicity 1
    • The rectangular plane is an even degree polynomial that opens upward.
      Answer to Exercise 26
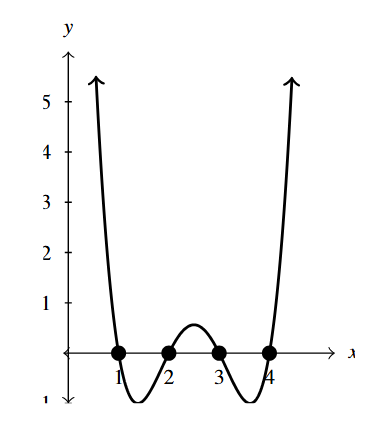
  27. [latex]Q(x) = (x + 5)^{2}(x - 3)^{4}[/latex]
    • [latex]x = -5[/latex] multiplicity 2
    • [latex]x = 3[/latex] multiplicity 4
    • The rectangular plane with an even degree polynomial that opens upward.
      Answer to Exercise 27
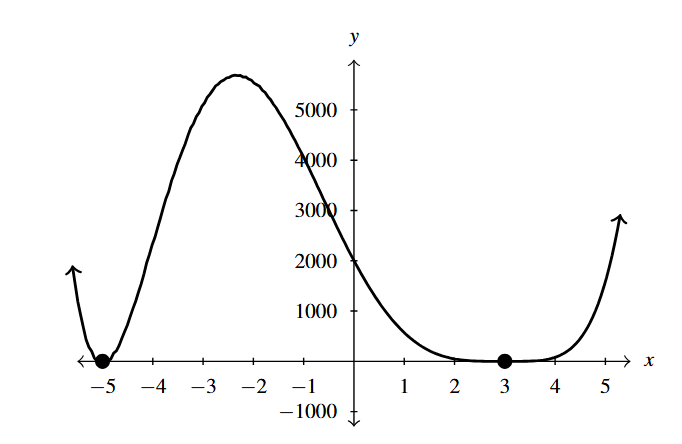
  28. [latex]f(t) = t^2(t-2)^2(t+2)^2[/latex]
    • [latex]t = -2[/latex] multiplicity 2
    • [latex]t = 0[/latex] multiplicity 2
    • [latex]t = 2[/latex] multiplicity 2
    • The rectangular plane with an even degree polynomial that opens upward.
      Answer to Exercise 28
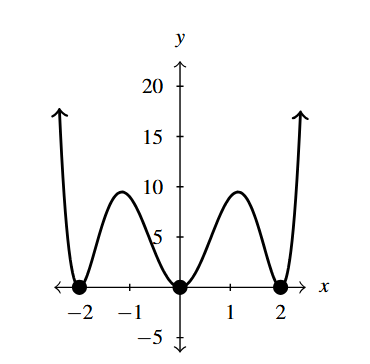
  29. [latex]H(z) = (3-z)\left(z^2+1\right)[/latex]
    • [latex]z=3[/latex] multiplicity 1
    • The rectangular plane with an odd degree polynomial that mostly decreases left to right.
      Answer to Exercise 29
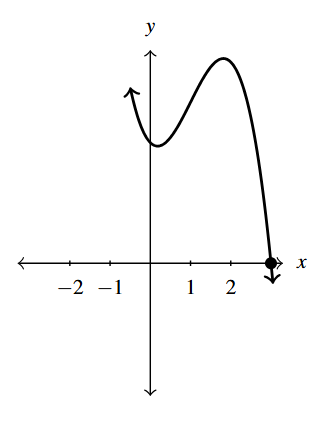
  30. [latex]Z(x) = x(42 - x^{2})[/latex]
    • [latex]x = -\sqrt{42}[/latex] multiplicity 1
    • [latex]x = 0[/latex] multiplicity 1
    • [latex]x = \sqrt{42}[/latex] multiplicity 1
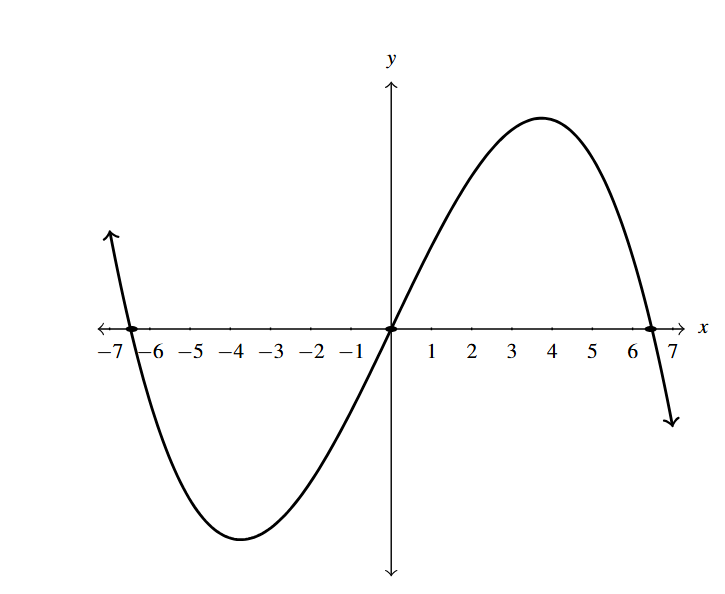
    • The rectangular plane with an odd degree polynomial that decreases left to right.
      Answer to Exercise 30
  31. odd
  32. neither
  33. even
  34. even
  35. even
  36. neither
  37. odd
  38. odd
  39. even
  40. odd
  41. neither
  42. even
  43. odd
  44. even
  45. even and odd
  46. Answer May Very
  47. a. even, b. odd, c. neither, d. odd[2]
  48. For [latex]f(x) = |x|[/latex], [latex]f(-x) = |-x| = |(-1) x| = |-1| |x| = (1) |x| = |x|[/latex]. Hence, [latex]f(-x) = f(x)[/latex].
  49. [latex]V(x) = x(8.5-2x)(11-2x) = 4x^3-39x^2+93.5x[/latex], 0 < [latex]x[/latex] < 4.25. Volume is maximized when [latex]x \approx 1.58[/latex], so we get the dimensions of the box with maximum volume are: height [latex]\approx[/latex] 1.58 inches, width [latex]\approx[/latex] 5.34 inches, and depth [latex]\approx[/latex] 7.84 inches. The maximum volume is [latex]\approx[/latex] 66.15 cubic inches.
  50. Each of these average rates of change indicate slope of the curve over the given interval. Smaller slopes correspond to flatter curves and higher slopes correspond to steeper curves.
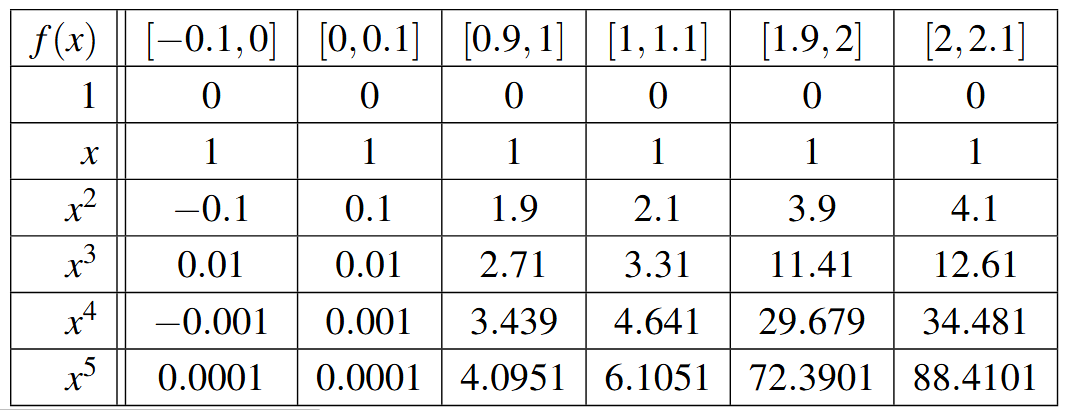
    The filled in graph for Exercise 50.
    Answer to Exercise 50
  51. As we sample points closer to [latex]x=1[/latex], the slope of the curve approaches the exponent on [latex]x[/latex].
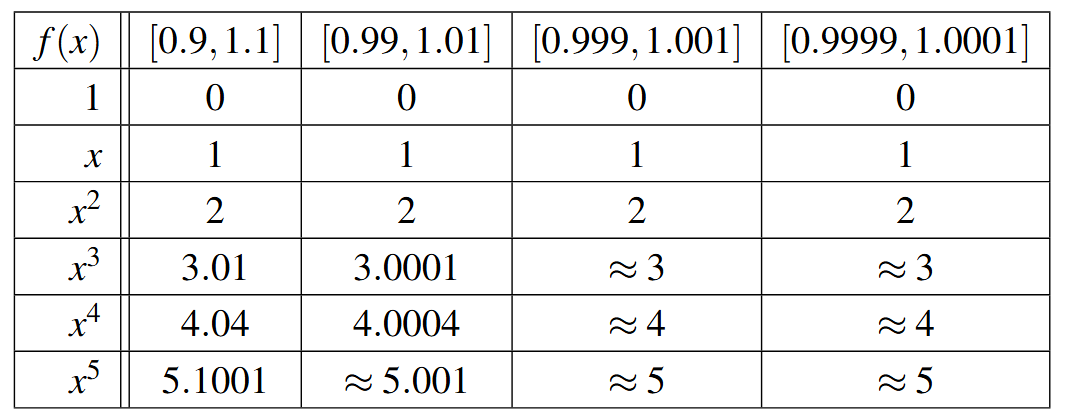
    The filled in table for Exercise 51.
    Answer to Exercise 51
  52. The calculator gives the location of the absolute maximum (rounded to three decimal places) as [latex]x \approx 6.305[/latex] and [latex]y \approx 1115.417[/latex]. because [latex]x[/latex] represents the number of TVs sold in hundreds, [latex]x = 6.305[/latex] corresponds to 630.5 TVs. because we can’t sell half of a TV, we compare [latex]R(6.30) \approx 1115.415[/latex] and [latex]R(6.31) \approx 1115.416[/latex], so selling 631 TVs results in a (slightly) higher revenue. because [latex]y[/latex] represents the revenue in thousands of dollars, the maximum revenue is $1,115,416.
  53. [latex]P(x) = R(x) - C(x) = -5x^3+35x^2-45x-25[/latex], [latex]0 \leq x \leq 10.07[/latex].
  54. The calculator gives the location of the absolute maximum (rounded to three decimal places) as [latex]x \approx 3.897[/latex] and [latex]y \approx 35.255[/latex]. because [latex]x[/latex] represents the number of TVs sold in hundreds, [latex]x = 3.897[/latex] corresponds to 389.7 TVs. because we can’t sell 0.7 of a TV, we compare [latex]P(3.89) \approx 35.254[/latex] and [latex]P(3.90) \approx 35.255[/latex], so selling 390 TVs results in a (slightly) higher revenue. because [latex]y[/latex] represents the revenue in thousands of dollars, the maximum revenue is $35,255.
  55. Making and selling 71 PortaBoys yields a maximized profit of $5910.67.
  56. .
    1. To maximize the volume, we assume we start with the maximum Length [latex]+[/latex] Girth of 130, so the length is [latex]130 - 4x[/latex]. The volume of a rectangular box is length [latex]\times[/latex] width [latex]\times[/latex] height so we get [latex]V(x) = x^{2}(130 - 4x) = -4x^{3} + 130x^{2}[/latex].
    2. Using a graphing utility, we get a (local) maximum of [latex]y = V(x)[/latex] at [latex](21.67, 20342.59)[/latex]. Hence, the maximum volume is [latex]20342.59 \text{in.}^{3}[/latex] using a box with dimensions 21.67 in. [latex]\times[/latex] 21.67 in. [latex]\times[/latex] 43.32 in.
    3. If we start with Length [latex]+[/latex] Girth [latex]= 108[/latex] then the length is [latex]108 - 4x[/latex] so [latex]V(x) = -4x^{3} + 108x^{2}[/latex]. Graphing [latex]y = V(x)[/latex] shows a (local) maximum at [latex](18.00, 11664.00)[/latex] so the dimensions of the box with maximum volume are 18.00 in. [latex]\times[/latex] 18.00 in. [latex]\times[/latex] 36 in. for a volume of [latex]11664.00\text{in.}^{3}[/latex]. (Calculus will confirm that the measurements which maximize the volume are \underline{exactly} 18in. by 18in. by 36in., however, as I’m sure you are aware by now, we treat all numerical results as approximations and list them as such.)
  57. .
    1. as [latex]x \rightarrow -\infty[/latex], [latex]p(x) \rightarrow -\infty[/latex] and as [latex]x \rightarrow \infty[/latex], [latex]p(x) \rightarrow -\infty[/latex]
    2. The zeros appear to be: [latex]x=-1.5[/latex], even multiplicity – probably 1 because it doesn’t look like the graph is very flat near [latex]x = 2[/latex]; [latex]x=0[/latex], odd multiplicity – probably 1 because the graph seems fairly linear as it passes through the origin; [latex]x=1[/latex] odd multiplicity – probably 3 or higher because the graph seems fairly flat near [latex]x = 1[/latex].
    3. local minimum: approximately [latex](-0.773, -2.888)[/latex]; local maximums: approximately [latex](-1.5,0)[/latex], and [latex](0.32, 0.532)[/latex]
    4. Based on the graph, even degree (at least 6 based on multiplicities) with a negative leading coefficient based on the end behavior.
    5. We only have a portion of the graph represented here.
  58. We are looking for the largest open interval containing [latex]x = -0.235[/latex] for which the graph of [latex]y = p(x)[/latex] is at or above [latex]y=-1.121[/latex]. because each of the gridlines on the [latex]x[/latex]-axis correspond to 0.2 units, we approximate this interval as [latex](-1.25[/latex]ish, 1.1ish[latex])[/latex].
  59. c. [latex]L(x) = x^2[/latex], d. [latex]L(x) = x+1[/latex]

Section 2.3 Answers

  1. quotient: [latex]5x-8[/latex], remainder: 9
  2. quotient: [latex]3y+15[/latex], remainder: 38
  3. quotient: 3, remainder: 18
  4. quotient: [latex]\dfrac{2}{3}[/latex], remainder: [latex]\dfrac{11}{3}[/latex]
  5. quotient: [latex]\dfrac{t}{2} - \dfrac{1}{4}[/latex], remainder: [latex]-\dfrac{15}{4}[/latex]
  6. quotient: [latex]\dfrac{w^2}{5} + \dfrac{2w}{5} + \dfrac{4}{5}[/latex], remainder: 0
  7. quotient: [latex]\dfrac{2}{3}[/latex], remainder: [latex]-x + \dfrac{1}{3}[/latex]
  8. quotient: [latex]2y^2+y+1[/latex], remainder: 0
  9. quotient: [latex]w[/latex], remainder: [latex]2w[/latex]
  10. quotient: [latex]5t[/latex], remainder: [latex]-21t + 1[/latex]
  11. quotient:[3] [latex]t^2 + t \sqrt[3]{4} + 2\sqrt[3]{2}[/latex], remainder: 0
  12. quotient: [latex]x -1 - \sqrt{2}[/latex], remainder: 0
  13. [latex]\left(3x^2-2x+1 \right) = \left(x-1\right) (3x+1)+2[/latex]
  14. [latex]\left(x^2-5 \right)= \left(x-5\right)(x+5) + 20[/latex]
  15. [latex]\left(3-4t-2t^2 \right) = \left(t+1\right)(-2t-2)+5[/latex]
  16. [latex]\left(4t^2-5t +3\right) = \left(t+3\right)(4t-17)+54[/latex]
  17. [latex]\left(z^3 + 8 \right) = \left(z+2\right) \left(z^2-2z+4\right) + 0[/latex]
  18. [latex]\left(4z^3 +2z-3 \right) = \left(z -3\right) \left(4z^2+12z+38\right) + 111[/latex]
  19. [latex]\left(18x^2-15x-25\right) = \left(x - \frac{5}{3} \right)(18x+15)+0[/latex]
  20. [latex]\left(4x^2-1 \right) = \left(x - \frac{1}{2} \right)(4x+2)+0[/latex]
  21. [latex]\left(2t^3+t^2+2t+1 \right) = \left(t + \frac{1}{2} \right)\left(2t^2+2\right)+0[/latex]
  22. [latex]\left(3t^3 - t + 4 \right) = \left(t - \frac{2}{3} \right) \left(3t^2+2t+\frac{1}{3}\right) + \frac{38}{9}[/latex]
  23. [latex]\left(2z^3 - 3z +1 \right) = \left(z - \frac{1}{2} \right) \left(2z^2+z-\frac{5}{2}\right)-\frac{1}{4}[/latex]
  24. [latex]\left(4z^4-12z^3+13z^2 -12z+9\right) = \left(z - \frac{3}{2} \right) \left(4z^3-6z^2+4z-6 \right)+0[/latex]
  25. [latex]\left(x^4-6x^2+9 \right) = \left(x -\sqrt{3} \right) \left(x^3+\sqrt{3} \,x^2-3x-3\sqrt{3}\right) + 0[/latex]
  26. [latex]\left(x^6-6x^4+12x^2-8\right) = \left(x +\sqrt{2} \right) \left(x^5-\sqrt{2} \, x^4-4x^3+4\sqrt{2} \, x^2+4x-4\sqrt{2}\right) + 0[/latex]
  27. [latex]x^{3} - 6x^{2} + 11x - 6 = (x - 1)(x - 2)(x - 3)[/latex]
  28. [latex]x^{3} - 24x^{2} + 192x - 512 = (x - 8)^{3}[/latex]
  29. [latex]3t^{3} + 4t^{2} - t - 2 = 3\left(t - \frac{2}{3}\right)(t + 1)^{2}[/latex]
  30. [latex]2t^3-3t^2-11t+6 = 2\left(t-\frac{1}{2}\right)(t+2)(t-3)[/latex]
  31. [latex]z^3+2z^2-3z-6 = (z+2)(z+\sqrt{3})(z-\sqrt{3})[/latex]
  32. [latex]2z^3-z^2-10z+5=2\left(z-\frac{1}{2}\right)(z+\sqrt{5})(z-\sqrt{5})[/latex]
  33. [latex]4x^{4} - 28x^{3} + 61x^{2} - 42x + 9 = 4\left(x - \frac{1}{2} \right)^{2}(x - 3)^{2}[/latex]
  34.  [latex]t^5+2t^4-12t^3-38t^2-37t-12 = (t+1)^3(t+3)(t-4)[/latex]
  35. [latex]125z^{5} - 275z^{4} - 2265z^{3} - 3213z^{2} - 1728z - 324[/latex] = [latex]125\left(z + \frac{3}{5} \right)^{3}(z + 2)(z - 6)[/latex]
  36. [latex]x^{2} - 2x - 2 = (x - (1 - \sqrt{3}))(x - (1 + \sqrt{3}))[/latex]

 

  1. You'll need to use your calculator to zoom in far enough to see that the vertex is not the [latex]y[/latex]-intercept. ↵
  2. You need to multiply out the express for [latex]g(x)[/latex] so it is in the form prescribed by Definition 2.7. ↵
  3. Note: [latex]\sqrt[3]{16} = 2\sqrt[3]{2}[/latex]. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Functions, Trigonometry, and Systems of Equations (Second Edition) Copyright © 2025 by Texas A&M Mathematics Department is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book