"

Section 3.1 Answers

  1. [latex]\dfrac{3(x+3)}{x(x+2)}[/latex], [latex]x \neq 3[/latex]
  2. [latex]\dfrac{t}{(3t+4)(t^2+1)}[/latex], [latex]t \neq 2[/latex]
  3. [latex]-\dfrac{y(y-3)}{y+4}[/latex], [latex]y \neq -\dfrac{1}{2}, 3, 4[/latex]
  4. [latex]\dfrac{2x-1}{3x-1}[/latex]
  5. [latex]-w-1[/latex], [latex]w \neq 1[/latex]
  6. [latex]\dfrac{y}{3}[/latex], [latex]y \neq 0[/latex]
  7. [latex]\dfrac{b^2-5b+7}{b-3}[/latex]
  8. [latex]\dfrac{4x^2+x+4}{(x-4)(2x+1)}[/latex]
  9. [latex]\dfrac{m+1}{m+2}[/latex], [latex]m \neq 2[/latex]
  10. [latex]-\dfrac{2}{x}[/latex], [latex]x \neq 1[/latex]
  11. [latex]\dfrac{3}{4-2h}[/latex], [latex]h \neq 0[/latex]
  12. [latex]-\dfrac{1}{x(x+h)}[/latex], [latex]h \neq 0[/latex]
  13. [latex]\dfrac{8}{3w}[/latex]
  14. [latex]-\dfrac{2(y^2-7y+9)}{y(y-3)^2}[/latex]
  15. [latex]-\dfrac{6}{(x-2)^2}[/latex]
  16. [latex]t^2+t[/latex], [latex]t \neq 0[/latex]
  17. [latex]-\dfrac{2(h+6)}{9(h+3)^2}[/latex], [latex]h \neq 0[/latex]
  18. [latex]\dfrac{1}{(7-x)(7-x-h)}[/latex], [latex]h \neq 0[/latex]
  19. 2, 2.
  20. [latex]-3[/latex], [latex]-3[/latex].
  21. 0, 0.
  22. [latex]3h+11[/latex], [latex]6x+3h-1[/latex]
  23. [latex]-h-2[/latex], [latex]-2x-h+2[/latex]
  24. [latex]4h+16[/latex], [latex]8x+4h[/latex]
  25. [latex]-h-3[/latex], [latex]-2x-h+1[/latex]
  26. [latex]h^2+6h+12[/latex], [latex]3x^{2} + 3xh + h^{2}[/latex]
  27. [latex]m[/latex], [latex]m[/latex]
  28. [latex]ah + 4a+b[/latex], [latex]2ax + ah + b[/latex]
  29. [latex]\dfrac{2}{\Delta x-1}[/latex], [latex]\dfrac{-2}{x(x+\Delta x)}[/latex]
  30. [latex]\dfrac{-3}{2(\Delta x - 2)}[/latex], [latex]\dfrac{3}{(x+\Delta x-1)(x-1)}[/latex]
  31. [latex]\dfrac{2-\Delta x}{(\Delta x - 1)^2}[/latex], [latex]\dfrac{-(2x+\Delta x)}{x^2(x+\Delta x)^2}[/latex]
  32. [latex]\dfrac{-1}{2(\Delta x+4)}[/latex], [latex]\dfrac{-2}{(x+5)(x+\Delta x+5)}[/latex]
  33. [latex]\dfrac{4}{7(4 \Delta x - 7)}[/latex], [latex]\dfrac{-4}{(4x-3)(4x+4\Delta x-3)}[/latex]
  34. [latex]\dfrac{6}{\Delta x + 1}[/latex], [latex]\dfrac{6}{(x+2)(x+\Delta x+2)}[/latex]
  35. [latex]\dfrac{9}{10(\Delta x - 10)}[/latex], [latex]\dfrac{-9}{(x - 9)(x + \Delta x - 9)}[/latex]
  36. [latex]\dfrac{\Delta x}{2 \Delta x - 1}[/latex], [latex]\dfrac{2x^2+2x\Delta x+2x+\Delta x}{(2x+1)(2x+2\Delta x+1)}[/latex]
  37. [latex]\dfrac{-1}{\sqrt{9-\Delta t} +3}[/latex], [latex]\dfrac{-1}{\sqrt{9-t-\Delta t} + \sqrt{9-t}}[/latex]
  38. [latex]\dfrac{2}{\sqrt{2\Delta t+1} + 1}[/latex], [latex]\dfrac{2}{\sqrt{2t+2\Delta t+1} + \sqrt{2t+1}}[/latex]
  39. [latex]\dfrac{-4}{\sqrt{5-4\Delta t} + \sqrt{5}}[/latex], [latex]\dfrac{-4}{\sqrt{-4t-4\Delta t+5} + \sqrt{-4t+5}}[/latex]
  40. [latex]\dfrac{-1}{\sqrt{4-\Delta t} + 2}[/latex], [latex]\dfrac{-1}{\sqrt{4-t-\Delta t} + \sqrt{4-t}}[/latex]
  41. [latex]\dfrac{a}{\sqrt{a\Delta t+b} + \sqrt{b}}[/latex], [latex]\dfrac{a}{\sqrt{at+a\Delta t+b} + \sqrt{at+b}}[/latex]
  42. [latex](\Delta t)^{\frac{1}{2}}[/latex], [latex]\dfrac{3t^2+3t\Delta t+(\Delta t)^2}{(t+\Delta t)^{3/2} + t^{3/2}}[/latex]
  43. [latex]\dfrac{1}{(\Delta t)^{2/3}}[/latex], [latex]\dfrac{1}{(t+\Delta t)^{2/3} + (t+\Delta t)^{1/3} t^{1/3} + t^{2/3}}[/latex]
  44. .
    1. Answers May Vary
    2. [latex](f_{+} + f_{-})(x) = f_{+}(x) + f_{-}(x) = \dfrac{f(x) + |f(x)|}{2} + \dfrac{f(x) - |f(x)|}{2} = \dfrac{2f(x)}{2} = f(x)[/latex].
    3. [latex]f_{+}(x) = \left\{ \begin{array}{lr} 0 & \text{ if } f(x) \text{   } 0 \\ f(x) & \text{ if } f(x) \geq 0 \\ \end{array} \right., \text{  and  }  f_{-}(x) = \left\{\begin{array}{lr} f(x) & \text{ if } f(x) \text{ } 0 \\ 0 & \text{ if } f(x) \geq 0 \\ \end{array} \right.[/latex]

Section 3.2 Answers

  1. [latex]4x^2+3x-1 = (x-3)(4x+15) + 44[/latex]
  2. [latex]2x^3-x+1 = \left(x^2+x+1\right)(2x-2)+(-x+3)[/latex]
  3. [latex]5x^{4} - 3x^{3} + 2x^{2} - 1 = \left(x^{2} + 4 \right) \left(5x^{2} - 3x - 18 \right) + (12x + 71)[/latex]
  4. [latex]-x^{5} + 7x^{3} - x = \left(x^{3} - x^{2} + 1 \right) \left(-x^{2} - x + 6 \right) + \left(7x^{2} - 6 \right)[/latex]
  5. [latex]9x^{3} + 5 =(2x - 3) \left(\frac{9}{2}x^{2} + \frac{27}{4}x + \frac{81}{8} \right) + \frac{283}{8}[/latex]
  6. [latex]4x^2 - x - 23 = \left(x^{2} - 1 \right)(4) + (-x - 19)[/latex]
  7. [latex]F(x) = \dfrac{1}{x-2}+1[/latex]
    • Domain: [latex](-\infty, 2) \cup (2, \infty)[/latex]
    • Range: [latex](-\infty, 1) \cup (1, \infty)[/latex]
    • Vertical asymptote: [latex]x = 2[/latex]
    • Horizontal asymptote: [latex]y = 1[/latex]
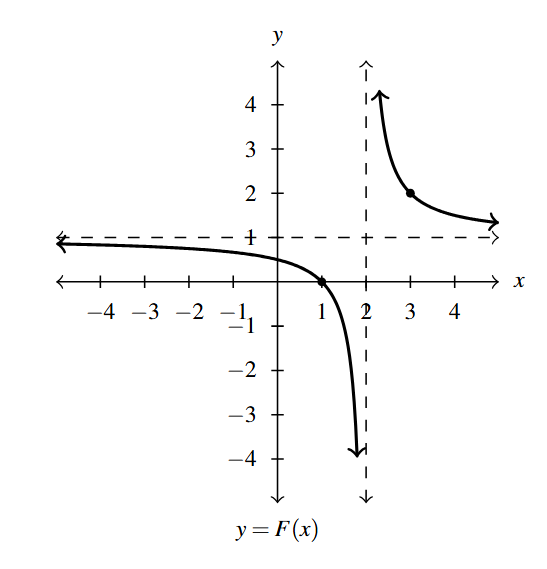
    • A rectangular plane with the graph of the rational function with a vertical asymptote of x = 2 and a horizontal asymptote of y = 1.
      Answer to Exercise 7
  8. [latex]F(x) = \dfrac{2x}{x+1} = \dfrac{-2}{x+1}+2[/latex]
    • Domain: [latex](-\infty, -1) \cup (-1, \infty)[/latex]
    • Range: [latex](-\infty, 2) \cup (2, \infty)[/latex]
    • Vertical asymptote: [latex]x = -1[/latex]
    • Horizontal asymptote: [latex]y = 2[/latex]
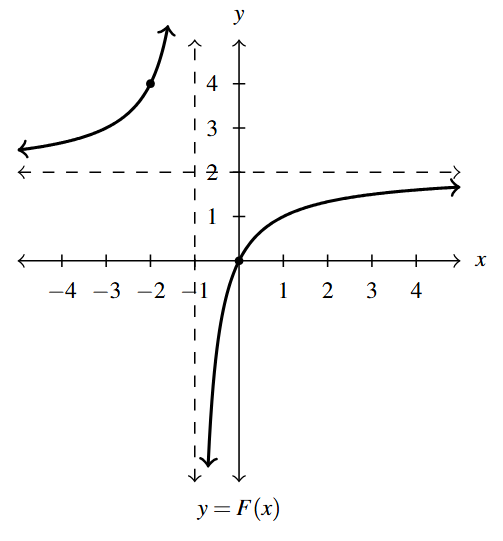
    • A rectangular plane with the graph of the rational function with a vertical asymptote of x = -1 and a horizontal asymptote of y = 2.
      Answer to Exercise 8
  9. [latex]F(x)=4x(2x+1)^{-1} = \dfrac{4x}{2x+1} = \dfrac{-1}{x+\frac{1}{2}}+2[/latex]
    • Domain: [latex]\left(-\infty, -\frac{1}{2} \right) \cup \left(-\frac{1}{2}, \infty \right)[/latex]
    • Range: [latex](-\infty, 2) \cup (2, \infty)[/latex]
    • Vertical asymptote: [latex]y= 2[/latex]
    • Horizontal asymptote: [latex]x = -\frac{1}{2}[/latex]
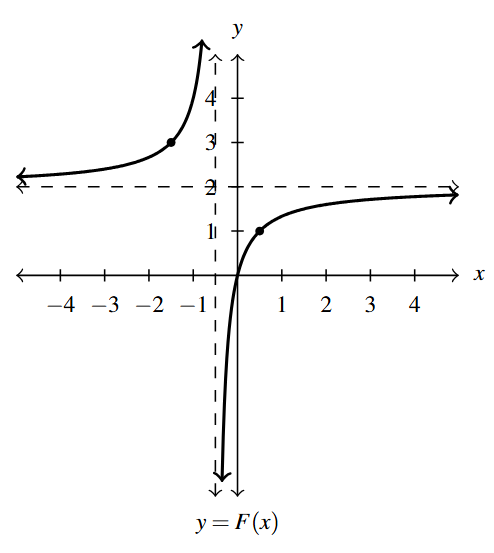
    • A rectangular plane with the graph of the rational function with a vertical asymptote of x = -1/2 and a horizontal asymptote of y = 2.
      Answer to Exercise 9
  10. [latex]F(x)=-(x-1)^{-2}+3 = \dfrac{-1}{(x-1)^2} + 3[/latex]
    • Domain: [latex](-\infty, 1) \cup (1, \infty)[/latex]
    • Range: [latex](-\infty, 3) \cup (3, \infty)[/latex]
    • Vertical asymptote: [latex]x = 1[/latex]
    • Horizontal asymptote: [latex]y = 3[/latex]
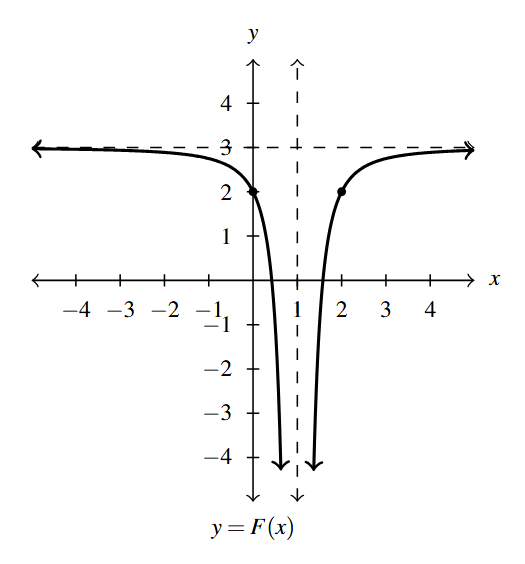
    • A rectangular plane with the graph of the rational function with a vertical asymptote of x = 1 and a horizontal asymptote of y = 3.
      Answer to Exercise 10
  11. [latex]F(x) = \dfrac{1}{x+2}-1[/latex]
  12. [latex]F(x) = \dfrac{-2}{x-1}+1[/latex]
  13. [latex]F(x) = \dfrac{-4}{(x+2)^2}+4[/latex]
  14. [latex]F(x) = \dfrac{1}{\left(x-\frac{1}{2}\right)^2}-4[/latex]
  15. [latex]f(x) = \dfrac{x}{3x - 6}[/latex]
    • Domain: [latex](-\infty, 2) \cup (2, \infty)[/latex]
    • Vertical asymptote: [latex]x = 2[/latex]
      • As [latex]x \rightarrow 2^{-}, f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow 2^{+}, f(x) \rightarrow \infty[/latex]
    • No holes in the graph
    • Horizontal asymptote: [latex]y = \frac{1}{3}[/latex]
      • As [latex]x \rightarrow -\infty, f(x) \rightarrow \frac{1}{3}^{-}[/latex]
      • As [latex]x \rightarrow \infty, f(x) \rightarrow \frac{1}{3}^{+}[/latex]
  16. [latex]f(x) = \dfrac{3 + 7x}{5 - 2x}[/latex]
    • Domain: [latex](-\infty, \frac{5}{2}) \cup (\frac{5}{2}, \infty)[/latex]
    • Vertical asymptote: [latex]x = \frac{5}{2}[/latex]
      • As [latex]x \rightarrow \frac{5}{2}^{-}, f(x) \rightarrow \infty[/latex]
      • As [latex]x \rightarrow \frac{5}{2}^{+}, f(x) \rightarrow -\infty[/latex]
    • No holes in the graph
    • Horizontal asymptote: [latex]y = -\frac{7}{2}[/latex]
      • As [latex]x \rightarrow -\infty, f(x) \rightarrow -\frac{7}{2}^{+}[/latex]
      • As [latex]x \rightarrow \infty, f(x) \rightarrow -\frac{7}{2}^{-}[/latex]
  17. [latex]f(x) = \dfrac{x}{x^{2} + x - 12} = \dfrac{x}{(x + 4)(x - 3)}[/latex]
    • Domain: [latex](-\infty, -4) \cup (-4, 3) \cup (3, \infty)[/latex]
    • Vertical asymptotes: [latex]x = -4, x = 3[/latex]
      • As [latex]x \rightarrow -4^{-}, f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow -4^{+}, f(x) \rightarrow \infty[/latex]
      • As [latex]x \rightarrow 3^{-}, f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow 3^{+}, f(x) \rightarrow \infty[/latex]
    • No holes in the graph
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]x \rightarrow -\infty, f(x) \rightarrow 0^{-}[/latex]
      • As [latex]x \rightarrow \infty, f(x) \rightarrow 0^{+}[/latex]
  18. [latex]g(t) = \dfrac{t}{t^{2} + 1}[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • No vertical asymptotes
    • No holes in the graph
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]t \rightarrow -\infty, g(t) \rightarrow 0^{-}[/latex]
      • As [latex]t \rightarrow \infty, g(t) \rightarrow 0^{+}[/latex]
  19. [latex]g(t) = \dfrac{t + 7}{(t + 3)^{2}}[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3, \infty)[/latex]
    • Vertical asymptote: [latex]t = -3[/latex]
      • As [latex]t \rightarrow -3^{-}, g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow -3^{+}, g(t) \rightarrow \infty[/latex]
    • No holes in the graph
    • Horizontal asymptote: [latex]y = 0[/latex][1]
      • As [latex]t \rightarrow -\infty, g(t) \rightarrow 0^{-}[/latex]
      • As [latex]t \rightarrow \infty, g(t) \rightarrow 0^{+}[/latex]
  20. [latex]g(t) = \dfrac{t^{3} + 1}{t^{2} - 1} = \dfrac{t^{2} - t+ 1}{t-1}[/latex]
    • Domain: [latex](-\infty, -1) \cup (-1, 1) \cup (1, \infty)[/latex]
    • Vertical asymptote: [latex]t = 1[/latex]
      • As [latex]t \rightarrow 1^{-}, g(t) \rightarrow -\infty[/latex]
      • As [latex]t \rightarrow 1^{+}, g(t) \rightarrow \infty[/latex]
    • Hole at [latex](-1, -\frac{3}{2})[/latex]
    • Slant asymptote: [latex]y=t[/latex]
      • As [latex]t \rightarrow -\infty[/latex], the graph is below [latex]y=t[/latex]
      • As [latex]t \rightarrow \infty[/latex], the graph is above [latex]y=t[/latex]
  21. [latex]r(z) = \dfrac{4z}{z^{2} + 4}[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • No vertical asymptotes
    • No holes in the graph
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]z \rightarrow -\infty, r(z) \rightarrow 0^{-}[/latex]
      • As [latex]z \rightarrow \infty, r(z) \rightarrow 0^{+}[/latex]
  22. [latex]r(z) = \dfrac{4z}{z^{2} -4} = \dfrac{4z}{(z + 2)(z - 2)}[/latex]
    • Domain: [latex](-\infty, -2) \cup (-2, 2) \cup (2, \infty)[/latex]
    • Vertical asymptotes: [latex]z = -2, z = 2[/latex]
      • As [latex]z \rightarrow -2^{-}, r(z) \rightarrow -\infty[/latex]
      • As [latex]z \rightarrow -2^{+}, r(z) \rightarrow \infty[/latex]
      • As [latex]z \rightarrow 2^{-}, r(z) \rightarrow -\infty[/latex]
      • As [latex]z \rightarrow 2^{+}, r(z) \rightarrow \infty[/latex]
    • No holes in the graph
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]z \rightarrow -\infty, r(z) \rightarrow 0^{-}[/latex]
      • As [latex]z \rightarrow \infty, r(z) \rightarrow 0^{+}[/latex]
  23. [latex]r(z) = \dfrac{z^2-z-12}{z^{2} +z - 6} = \dfrac{z-4}{z - 2}[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3, 2) \cup (2, \infty)[/latex]
    • Vertical asymptote: [latex]z = 2[/latex]
      • As [latex]z \rightarrow 2^{-}, r(z) \rightarrow \infty[/latex]
      • As [latex]z \rightarrow 2^{+}, r(z) \rightarrow -\infty[/latex]
    • Hole at [latex]\left(-3, \frac{7}{5} \right)[/latex]
    • Horizontal asymptote: [latex]y = 1[/latex]
      • As [latex]z \rightarrow -\infty, r(z) \rightarrow 1^{+}[/latex]
      • As [latex]z \rightarrow \infty, r(z) \rightarrow 1^{-}[/latex]
  24. [latex]f(x) = \dfrac{3x^2-5x-2}{x^{2} -9} = \dfrac{(3x+1)(x-2)}{(x + 3)(x - 3)}[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3, 3) \cup (3, \infty)[/latex]
    • Vertical asymptotes: [latex]x = -3, x = 3[/latex]
      • As [latex]x \rightarrow -3^{-}, f(x) \rightarrow \infty[/latex]
      • As [latex]x \rightarrow -3^{+}, f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow 3^{-}, f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow 3^{+}, f(x) \rightarrow \infty[/latex]
    • No holes in the graph
    • Horizontal asymptote: [latex]y = 3[/latex]
      • As [latex]x \rightarrow -\infty, f(x) \rightarrow 3^{+}[/latex]
      • As [latex]x \rightarrow \infty, f(x) \rightarrow 3^{-}[/latex]
  25. [latex]f(x) = \dfrac{x^3+2x^2+x}{x^{2} -x-2} = \dfrac{x(x+1)}{x - 2}[/latex]
    • Domain: [latex](-\infty, -1) \cup (-1, 2) \cup (2, \infty)[/latex]
    • Vertical asymptote: [latex]x = 2[/latex]
      • As [latex]x \rightarrow 2^{-}, f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow 2^{+}, f(x) \rightarrow \infty[/latex]
    • Hole at [latex](-1,0)[/latex]
    • Slant asymptote: [latex]y=x+3[/latex]
      • As [latex]x \rightarrow -\infty[/latex], the graph is below [latex]y=x+3[/latex]
      • As [latex]x \rightarrow \infty[/latex], the graph is above [latex]y=x+3[/latex]
  26. [latex]f(x) = \dfrac{x^3-3x+1}{x^2+1}[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • No vertical asymptotes
    • No holes in the graph
    • Slant asymptote: [latex]y=x[/latex]
      • As [latex]x \rightarrow -\infty[/latex], the graph is above [latex]y=x[/latex]
      • As [latex]x \rightarrow \infty[/latex], the graph is below [latex]y=x[/latex]
  27. [latex]g(t) = \dfrac{2t^{2} + 5t - 3}{3t + 2}[/latex]
    • Domain: [latex]\left(-\infty, -\frac{2}{3}\right) \cup \left(-\frac{2}{3}, \infty\right)[/latex]
    • Vertical asymptote: [latex]t = -\frac{2}{3}[/latex]
      • As [latex]t \rightarrow -\frac{2}{3}^{-}, g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow -\frac{2}{3}^{+}, g(t) \rightarrow -\infty[/latex]
    • No holes in the graph
    • Slant asymptote: [latex]y = \frac{2}{3}t + \frac{11}{9}[/latex]
      • As [latex]t \rightarrow -\infty[/latex], the graph is above [latex]y = \frac{2}{3}t + \frac{11}{9}[/latex]
      • As [latex]t \rightarrow \infty[/latex], the graph is below [latex]y = \frac{2}{3}t + \frac{11}{9}[/latex]
  28. [latex]g(t) = \dfrac{-t^{3} + 4t}{t^{2} - 9} = \dfrac{-t^{3} + 4t}{(t-3)(t+3)}[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3, 3) \cup (3, \infty)[/latex]
    • Vertical asymptotes: [latex]t = -3[/latex], [latex]t=3[/latex]
      • As [latex]t \rightarrow -3^{-}, g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow -3^{+}, g(t) \rightarrow -\infty[/latex]
      • As [latex]t \rightarrow 3^{-}, g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow 3^{+}, g(t) \rightarrow -\infty[/latex]
    • No holes in the graph
    • Slant asymptote: [latex]y=-t[/latex]
      • As [latex]t \rightarrow -\infty[/latex], the graph is above [latex]y=-t[/latex]
      • As [latex]t \rightarrow \infty[/latex], the graph is below [latex]y=-t[/latex]
  29. [latex]g(t) = \dfrac{-5t^{4} - 3t^{3} + t^{2} - 10}{t^{3} - 3t^{2} + 3t - 1} =\dfrac{-5t^{4} - 3t^{3} + t^{2} - 10}{(t-1)^3}[/latex]
    • Domain: [latex](-\infty, 1) \cup (1, \infty)[/latex]
    • Vertical asymptotes: [latex]t = 1[/latex]
      • As [latex]t \rightarrow 1^{-}, g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow 1^{+}, g(t) \rightarrow -\infty[/latex]
    • No holes in the graph
    • Slant asymptote: [latex]y=-5t-18[/latex]
      • As [latex]t \rightarrow -\infty[/latex], the graph is above [latex]y=-5t-18[/latex]
      • As [latex]t \rightarrow \infty[/latex], the graph is below [latex]y=-5t-18[/latex]
  30. [latex]r(z) = \dfrac{z^3}{1-z}[/latex]
    • Domain: [latex](-\infty, 1) \cup (1, \infty)[/latex]
    • Vertical asymptote: [latex]z=1[/latex]
      • As [latex]z \rightarrow 1^{-}, r(z) \rightarrow \infty[/latex]
      • As [latex]z \rightarrow 1^{+}, r(z) \rightarrow -\infty[/latex]
    • No holes in the graph
    • No horizontal or slant asymptote
      • As [latex]z \rightarrow -\infty[/latex], [latex]r(z) \rightarrow -\infty[/latex]
      • As [latex]z \rightarrow \infty[/latex], [latex]r(z) \rightarrow -\infty[/latex]
  31. [latex]r(z) = \dfrac{18-2z^2}{z^2-9} = -2[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3,3) \cup (3, \infty)[/latex]
    • No vertical asymptotes
    • Holes in the graph at [latex](-3,-2)[/latex] and [latex](3,-2)[/latex]
    • Horizontal asymptote [latex]y = -2[/latex]
      • As [latex]z \rightarrow \pm \infty[/latex], [latex]r(z) = -2[/latex]
  32. [latex]r(z) = \dfrac{z^3-4z^2-4z-5}{z^2+z+1} = z-5[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • No vertical asymptotes
    • No holes in the graph
    • Slant asymptote: [latex]y = z-5[/latex]
    • [latex]r(z) = z-5[/latex] everywhere.
  33. .
    1. [latex]C(25) = 590[/latex] means it costs \$590 to remove 25% of the fish and and [latex]C(95)= 33630[/latex] means it would cost \$33630 to remove 95% of the fish from the pond.
    2. The vertical asymptote at [latex]x = 100[/latex] means that as we try to remove 100% of the fish from the pond, the cost increases without bound; i.e., it’s impossible to remove all of the fish.
    3. For \$40000 you could remove about 95.76% of the fish.
  34. .
    1. [latex]\overline{v}(t) = \frac{s(t) - s(5)}{t - 5} = \frac{-5t^2+100t-375}{t-5} = -5t+75[/latex], [latex]t \neq 5[/latex]. The instantaneous velocity of the rocket when [latex]t_{0} = 5[/latex] is [latex]-5(5)+75 = 50[/latex] meaning it is traveling 50 feet per second upwards.
    2. [latex]\overline{v}(t) = \frac{s(t) - s(9)}{t - 9} = \frac{-5t^2+100t-495}{t-9} = -5t+55[/latex], [latex]t \neq 9[/latex]. The instantaneous velocity of the rocket when [latex]t_{0} = 9[/latex] is [latex]-5(9)+55 = 10[/latex], so the rocket has slowed to 10. feet per second (but still heading up.)
    3. [latex]\overline{v}(t) = \frac{s(t) - s(10)}{t - 10} = \frac{-5t^2+100t-495}{t-10} = -5t+50[/latex], [latex]t \neq 10[/latex]. The instantaneous velocity of the rocket when [latex]t_{0} = 10[/latex] is [latex]-5(10)+50 = 0[/latex], so the rocket has momentarily stopped! In a previous example, we learned the rocket reaches its maximum height when [latex]t = 10[/latex] seconds, which means the rocket must change direction from heading up to coming back down, so it makes sense that for this instant, its velocity is 0.
    4. [latex]\overline{v}(t) = \frac{s(t) - s(11)}{t - 11} = \frac{-5t^2+100t-495}{t-11} = -5t+45[/latex], [latex]t \neq 11[/latex]. The instantaneous velocity of the rocket when [latex]t_{0} = 11[/latex] is [latex]-5(11)+45 = -10[/latex] meaning the rocket has, indeed, changed direction and is heading downwards at a rate of [latex]10[/latex] feet per second. (Note the symmetry here between this answer and our answer when [latex]t=9[/latex].)
  35. The horizontal asymptote of the graph of [latex]P(t) = \frac{150t}{t + 15}[/latex] is [latex]y = 150[/latex] and it means that the model predicts the population of Sasquatch in Portage County will never exceed 150.
  36. .
    1. [latex]\overline{C}(x) = \frac{100x+2000}{x} = 100 + \frac{2000}{x}[/latex], [latex]x > 0[/latex].
    2. [latex]\overline{C}(1) = 2100[/latex] and [latex]\overline{C}(100) = 120[/latex]. When just 1 dOpi is produced, the cost per dOpi is \$2100, but when 100 dOpis are produced, the cost per dOpi is \$120.
    3. [latex]\overline{C}(x) = 200[/latex] when [latex]x = 20[/latex]. So to get the cost per dOpi to \$200, 20 dOpis need to be produced.
    4. As [latex]x \rightarrow 0^{+}[/latex], [latex]\overline{C}(x) \rightarrow \infty[/latex]. This means that as fewer and fewer dOpis are produced, the cost per dOpi becomes unbounded. In this situation, there is a fixed cost of \$2000 ([latex]C(0) = 2000[/latex]), we are trying to spread that \$2000 over fewer and fewer dOpis.
    5. As [latex]x \rightarrow \infty[/latex], [latex]\overline{C}(x) \rightarrow 100^{+}[/latex]. This means that as more and more dOpis are produced, the cost per dOpi approaches \$100, but is always a little more than \$100. Since \$100 is the variable cost per dOpi ([latex]C(x) = \underline{100}x+2000[/latex]), it means that no matter how many dOpis are produced, the average cost per dOpi will always be a bit higher than the variable cost to produce a dOpi. As before, we can attribute this to the \$2000 fixed cost, which factors into the average cost per dOpi no matter how many dOpis are produced.
  37. .
    1. The cost to make 0 items is [latex]C(0) = m(0)+b = b[/latex]. Hence, so the fixed costs are [latex]b[/latex].
    2. [latex]C(x) = mx+b[/latex] is a linear function with slope [latex]m>0[/latex]. Hence, the cost increases at a rate of [latex]m[/latex] dollars per item made. Hence, the variable cost is [latex]m[/latex].
    3. [latex]\overline{C}(x) = \frac{C(x)}{x} = \frac{mx+b}{x} = m + \frac{b}{x}[/latex] for [latex]x > 0[/latex].
    4. Since [latex]b>0[/latex], [latex]\overline{C}(x) = m + \frac{b}{x} > m[/latex] for [latex]x > 0[/latex]. As [latex]x \rightarrow \infty[/latex], [latex]\frac{b}{x} \rightarrow 0[/latex] so [latex]\overline{C}(x) = m + \frac{b}{x} \rightarrow m[/latex].
    5. Geometrically, the graph of [latex]y = \overline{C}(x)[/latex] has a horizontal asymptote [latex]y = m[/latex], the variable cost. In terms of costs, as more items are produced, the affect of the fixed cost on the average cost, [latex]\frac{b}{x}[/latex] falls away so that the average cost per item approaches the variable cost to make each item.
  38. If [latex]p(x) = mx + b[/latex] and [latex]C(x)[/latex] is linear, say [latex]C(x) = rx+s[/latex], then we can compute the the profit function (in general) as: [latex]P(x) = xp(x) - C(x) = x(mx+b) - (rx+s)[/latex] which simplifies to [latex]P(x) = mx^2 + (b-r)x -s[/latex]. Hence, the average profit [latex]\overline{P}(x) = \frac{P(x)}{x} = \frac{mx^2 + (b-r)x -s}{x} = mx + (b-r) - \frac{s}{x}[/latex]. We see that as [latex]x \rightarrow \infty[/latex], [latex]\frac{s}{x} \rightarrow 0[/latex] so [latex]\overline{P}(x) \approx mx + (b-r)[/latex]. Hence, [latex]y = mx + (b-r)[/latex] is the slant asymptote to [latex]y = \overline{P}(x)[/latex]. This means that as more items are sold, the average profit is decreasing at approximately the same rate as the price function is decreasing, [latex]m[/latex] dollars per item. That is, to sell one additional item, we drop the price [latex]p(x)[/latex] by [latex]m[/latex] dollars which results in a drop in the average profit by approximately [latex]m[/latex] dollars.
  39. .
    1. Answers May Vary
    2. The maximum power is approximately [latex]1.603 \; mW[/latex] which corresponds to [latex]3.9 \; k\Omega[/latex].
    3. As [latex]x \rightarrow \infty, \; P(x) \rightarrow 0^{+}[/latex] which means as the resistance increases without bound, the power diminishes to zero.
  40. [latex]a = -2[/latex] and [latex]c = -18[/latex] so [latex]f(x) = \dfrac{-2x^2+18}{x+3}[/latex].
  41. .
    1. [latex]a=6[/latex] and [latex]n=2[/latex] so [latex]f(x) = \dfrac{6x^{2} -4}{2x^2+1}[/latex]
    2. [latex]a=10[/latex] and [latex]n = 3[/latex] so [latex]f(x) = \dfrac{10x^{3} -4}{2x^2+1}[/latex]
  42. If we define [latex]f(x) = p(x) - p(a)[/latex] then [latex]f[/latex] is a polynomial function with [latex]f(a) = p(a) - p(a) = 0[/latex]. The Factor Theorem guarantees [latex](x-a)[/latex] is a factor of [latex]f(x)[/latex], that is, [latex]f(x) = p(x) - p(a) = (x-a)q(x)[/latex] for some polynomial [latex]q(x)[/latex]. Hence, [latex]r(x) = \frac{p(x)-p(a)}{x-a} = \frac{(x-a)q(x)}{x-a} = q(x)[/latex] so the graph of [latex]y = r(x)[/latex] is the same as the graph of the polynomial [latex]y = q(x)[/latex] except for a hole when [latex]x = a[/latex].
  43. The slope of the curves near [latex]x=1[/latex] matches the exponent on [latex]x[/latex].
    A table with five rows and five columns. The first row is the header row: f(x), [0.9, 1.1], [0.99, 1.01], [0.999, 1.001], and [0.9999,1.0001]. The first column is x raised to the negative 1, then x raised to the negative 2, then x raised to the negative 3, and last x raised to the negative 4. The table is filled in.
    Answer for Exercise 43

Section 3.3 Answers

  1. [latex]f(x) = \dfrac{4}{x + 2}[/latex]
    • Domain: [latex](-\infty, -2) \cup (-2, \infty)[/latex]
    • No [latex]x[/latex]-intercepts
    • [latex]y[/latex]-intercept: [latex](0, 2)[/latex]
    • Vertical asymptote: [latex]x = -2[/latex]
      • As [latex]x \rightarrow -2^{-}, \; f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow -2^{+}, \; f(x) \rightarrow \infty[/latex]
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}[/latex]
      • As [latex]x \rightarrow \infty, \; f(x) \rightarrow 0^{+}[/latex]
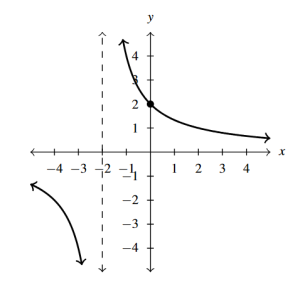
    • The rectangular plane with a rational function that as a vertical asymptote at x=-2 and decreases on both sides of the asymptote.
      Answer to Exercise 1
  2. [latex]f(x) = 5x(6-2x)^{-1} = \dfrac{5x}{6 - 2x}[/latex]
    • Domain: [latex](-\infty, 3) \cup (3, \infty)[/latex]
    • [latex]x[/latex]-intercept: [latex](0, 0)[/latex]
    • [latex]y[/latex]-intercept: [latex](0, 0)[/latex]
    • Vertical asymptote: [latex]x = 3[/latex]
      • As [latex]x \rightarrow 3^{-}, \; f(x) \rightarrow \infty[/latex]
      • As [latex]x \rightarrow 3^{+}, \; f(x) \rightarrow -\infty[/latex]
    • Horizontal asymptote: [latex]y = -\frac{5}{2}[/latex]
      • As [latex]x \rightarrow -\infty, \; f(x) \rightarrow -\frac{5}{2}^{+}[/latex]
      • As [latex]x \rightarrow \infty, \; f(x) \rightarrow -\frac{5}{2}^{-}[/latex]
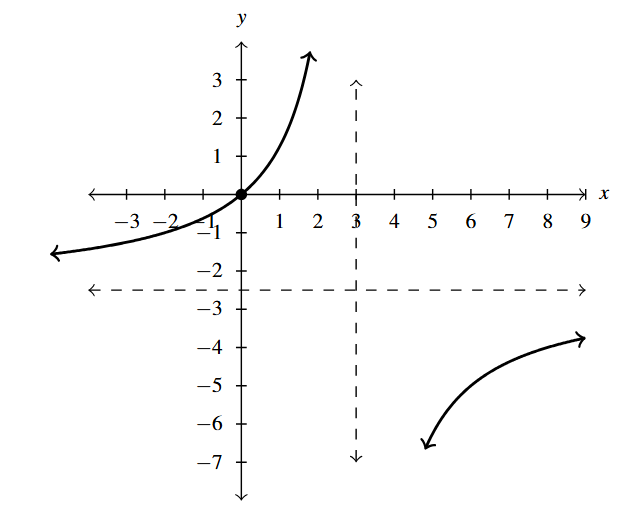
    • The rectangular plane with a rational function that as a vertical asymptote at x=3 and increases on both sides of the asymptote. The horizontal asymptote at approximately y=-2.5.
      Answer to Exercise 2
  3. [latex]g(t) = t^{-2} = \dfrac{1}{t^{2}}[/latex]
    • Domain: [latex](-\infty, 0) \cup (0, \infty)[/latex]
    • No [latex]t[/latex]-intercepts
    • No [latex]y[/latex]-intercepts
    • Vertical asymptote: [latex]t = 0[/latex]
      • As [latex]t \rightarrow 0^{-}, \; g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow 0^{+}, \; g(t) \rightarrow \infty[/latex]
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]t \rightarrow -\infty, \; g(t) \rightarrow 0^{+}[/latex]
      • As [latex]t \rightarrow \infty, \; g(t) \rightarrow 0^{+}[/latex]
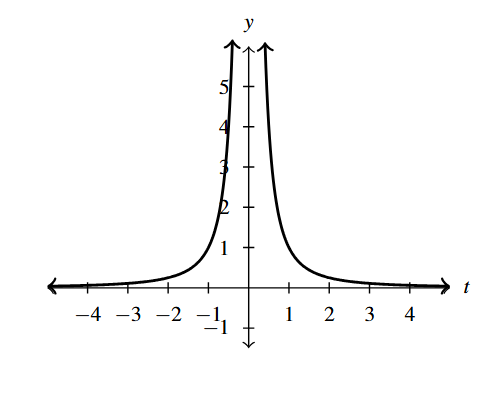
    • The rectangular plane with a rational function that as a vertical asymptote at x=0 that increases in the first part and decreases in the second.
      Answer to Exercise 3
  4. [latex]g(t) = \dfrac{1}{t^{2} + t - 12} = \dfrac{1}{(t - 3)(t + 4)}[/latex]
    • Domain: [latex](-\infty, -4) \cup (-4, 3) \cup (3, \infty)[/latex]
    • No [latex]t[/latex]-intercepts
    • [latex]y[/latex]-intercept: [latex](0, -\frac{1}{12})[/latex]
    • Vertical asymptotes: [latex]t = -4[/latex] and [latex]t = 3[/latex]
      • As [latex]t \rightarrow -4^{-}, \; g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow -4^{+}, \; g(t) \rightarrow -\infty[/latex]
      • As [latex]t \rightarrow 3^{-}, \; g(t) \rightarrow -\infty[/latex]
      • As [latex]t \rightarrow 3^{+}, \; g(t) \rightarrow \infty[/latex]
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]t \rightarrow -\infty, \; g(t) \rightarrow 0^{+}[/latex]
      • As [latex]t \rightarrow \infty, \; g(t) \rightarrow 0^{+}[/latex]
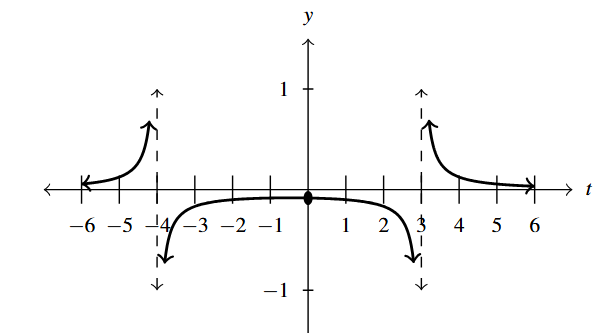
    • The rectangular plane with a rational function that has two vertical asymptotes at x = -4 and x =3. The function is in three parts.
      Answer to Exercise 4
  5. [latex]r(z) = \dfrac{2z - 1}{-2z^{2} - 5z + 3} = -\dfrac{2z - 1}{(2z - 1)(z + 3)}[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3, \frac{1}{2}) \cup (\frac{1}{2}, \infty)[/latex]
    • No [latex]z[/latex]-intercepts
    • [latex]y[/latex]-intercept: [latex](0, -\frac{1}{3})[/latex]
    • [latex]r(z) = \dfrac{-1}{z + 3}, \; z \neq \frac{1}{2}[/latex]
    • Hole in the graph at [latex](\frac{1}{2}, -\frac{2}{7})[/latex]
    • Vertical asymptote: [latex]z = -3[/latex]
      • As [latex]z \rightarrow -3^{-}, \; r(z) \rightarrow \infty[/latex]
      • As [latex]z \rightarrow -3^{+}, \; r(z) \rightarrow -\infty[/latex]
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]z \rightarrow -\infty, \; r(z) \rightarrow 0^{+}[/latex]
      • As [latex]z \rightarrow \infty, \; r(z) \rightarrow 0^{-}[/latex]
    • The rectangular plane with a rational function that has a vertical asymptote at x=-3 and a hole in the graph at approximately (0.5,-0.75). All parts increases left to right.
      Answer to Exercise 5
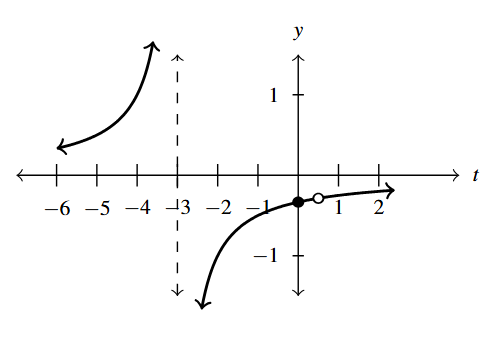
  6. [latex]r(z) = \dfrac{z}{z^{2} + z - 12} = \dfrac{z}{(z - 3)(z + 4)}[/latex]
    • Domain: [latex](-\infty, -4) \cup (-4, 3) \cup (3, \infty)[/latex]
    • [latex]z[/latex]-intercept: [latex](0, 0)[/latex]
    • [latex]y[/latex]-intercept: [latex](0, 0)[/latex]
    • Vertical asymptotes: [latex]z = -4[/latex] and [latex]z = 3[/latex]
      • As [latex]z \rightarrow -4^{-}, \; r(z) \rightarrow -\infty[/latex]
      • As [latex]z \rightarrow -4^{+}, \; r(z) \rightarrow \infty[/latex]
      • As [latex]z \rightarrow 3^{-}, \; r(z) \rightarrow -\infty[/latex]
      • As [latex]z \rightarrow 3^{+}, \; r(z) \rightarrow \infty[/latex]
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]z \rightarrow -\infty, \; r(z) \rightarrow 0^{-}[/latex]
      • As [latex]z \rightarrow \infty, \; r(z) \rightarrow 0^{+}[/latex]
    • The rectangular plane with a rational function that has two vertical asymptotes at x = -4 and x =3. The function is in three parts. All parts decrease left to right.
      Answer to Exercise 6
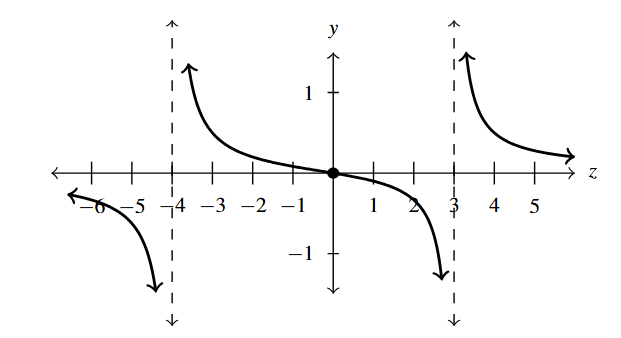
  7. [latex]f(x) = 4x(x^2+4)^{-1} = \dfrac{4x}{x^{2} + 4}[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • [latex]x[/latex]-intercept: [latex](0,0)[/latex]
    • [latex]y[/latex]-intercept: [latex](0,0)[/latex]
    • No vertical asymptotes
    • No holes in the graph
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]x \rightarrow -\infty, f(x) \rightarrow 0^{-}[/latex]
      • As [latex]x \rightarrow \infty, f(x) \rightarrow 0^{+}[/latex]
    • The rectangular plane with a rational function that contains no asymptotes. The curve decreases to approximately (-2,-1) and then increases to approximately (1.5,1) and then decreases again.
      Answer to Exercise 7
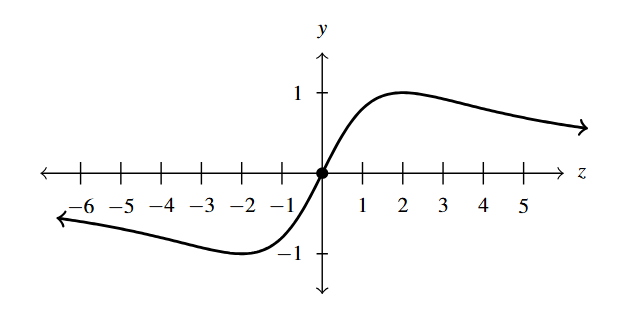
  8. [latex]f(x) = 4x(x^2-4)^{-1} = \dfrac{4x}{x^{2} -4} = \dfrac{4x}{(x + 2)(x - 2)}[/latex]
    • Domain: [latex](-\infty, -2) \cup (-2, 2) \cup (2, \infty)[/latex]
    • [latex]x[/latex]-intercept: [latex](0,0)[/latex]
    • [latex]y[/latex]-intercept: [latex](0,0)[/latex]
    • Vertical asymptotes: [latex]x = -2, x = 2[/latex]
      • As [latex]x \rightarrow -2^{-}, f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow -2^{+}, f(x) \rightarrow \infty[/latex]
      • As [latex]x \rightarrow 2^{-}, f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow 2^{+}, f(x) \rightarrow \infty[/latex]
    • No holes in the graph
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]x \rightarrow -\infty, f(x) \rightarrow 0^{-}[/latex]
      • As [latex]x \rightarrow \infty, f(x) \rightarrow 0^{+}[/latex]
    • The rectangular plane with a rational function that has two vertical asymptotes at x = -2 and x =2. The function is in three parts. All parts decrease left to right.
      Answer to Exercise 8
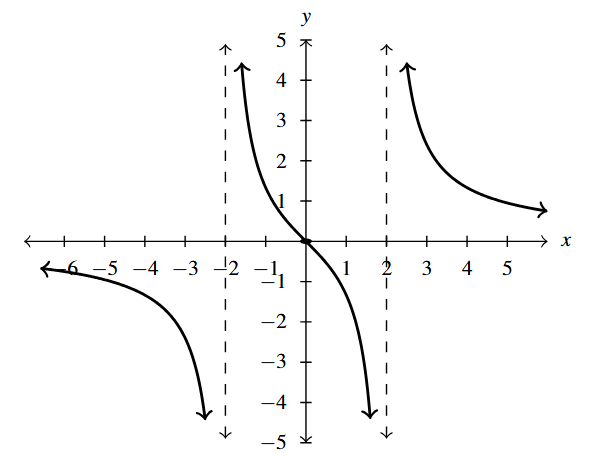
  9. [latex]g(t) = \dfrac{t^2-t-12}{t^{2} +t - 6} = \dfrac{t-4}{t - 2}, \, t \neq -3[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3, 2) \cup (2, \infty)[/latex]
    • [latex]t[/latex]-intercept: [latex](4,0)[/latex]
    • [latex]y[/latex]-intercept: [latex](0,2)[/latex]
    • Vertical asymptote: [latex]t = 2[/latex]
      • As [latex]t \rightarrow 2^{-}, g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow 2^{+}, g(t) \rightarrow -\infty[/latex]
    • Hole at [latex]\left(-3, \frac{7}{5} \right)[/latex]
    • Horizontal asymptote: [latex]y = 1[/latex]
      • As [latex]t \rightarrow -\infty, g(t) \rightarrow 1^{+}[/latex]
      • As [latex]t \rightarrow \infty, g(t) \rightarrow 1^{-}[/latex]
    • The rectangular plane with a rational function that has a vertical asymptote at x-2 and a horizontal asymptote at y=2.
      Answer to Exercise 9
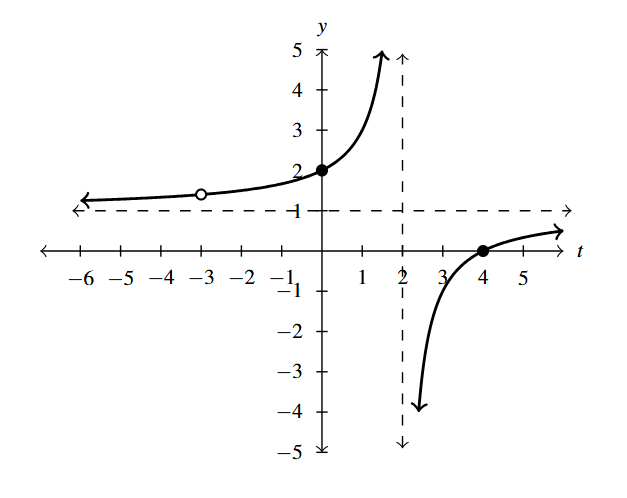
  10. [latex]g(t) = 3- \dfrac{5t-25}{t^2-9} = \dfrac{3t^2-5t-2}{t^{2} -9} = \dfrac{(3t+1)(t-2)}{(t + 3)(t - 3)}[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3, 3) \cup (3, \infty)[/latex]
    • [latex]t[/latex]-intercepts: [latex]\left(-\frac{1}{3}, 0 \right)[/latex], [latex](2,0)[/latex]
    • [latex]y[/latex]-intercept: [latex]\left(0, \frac{2}{9} \right)[/latex]
    • Vertical asymptotes: [latex]t = -3, t = 3[/latex]
      • As [latex]t \rightarrow -3^{-}, g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow -3^{+}, g(t) \rightarrow -\infty[/latex]
      • As [latex]t \rightarrow 3^{-}, g(t) \rightarrow -\infty[/latex]
      • As [latex]t \rightarrow 3^{+}, g(t) \rightarrow \infty[/latex]
    • Horizontal asymptote: [latex]y = 3[/latex]
      • As [latex]t \rightarrow -\infty, g(t) \rightarrow 3^{+}[/latex]
      • As [latex]t \rightarrow \infty, g(t) \rightarrow 3^{-}[/latex]
    • The rectangular plane with a rational function that has two vertical asymptotes at x=-3 and x=3. The curve also has a horizontal asymptote at y=3.
      Answer to Exercise 10
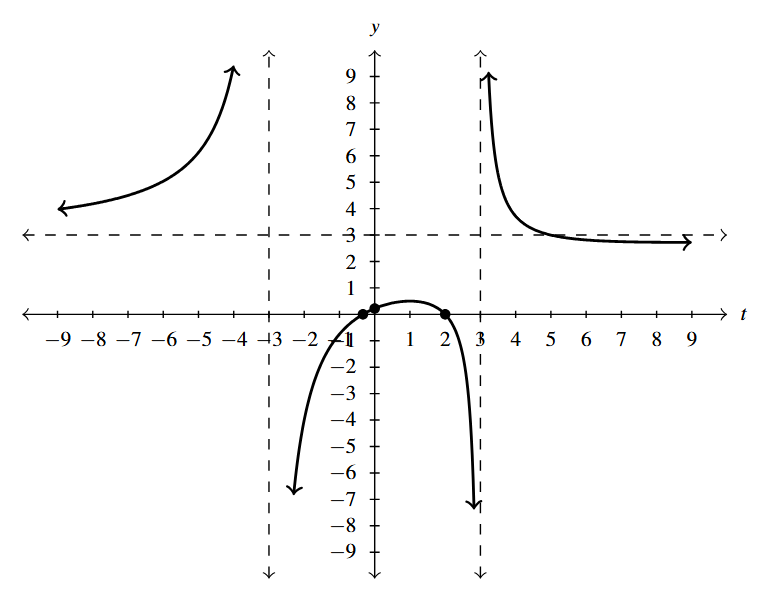
  11. [latex]r(z) = \dfrac{z^2-z-6}{z+1} = \dfrac{(z-3)(z+2)}{z+1}[/latex]
    • Domain: [latex](-\infty, -1) \cup (-1, \infty)[/latex]
    • [latex]z[/latex]-intercepts: [latex](-2,0)[/latex], [latex](3,0)[/latex]
    • [latex]y[/latex]-intercept: [latex](0,-6)[/latex]
    • Vertical asymptote: [latex]z = -1[/latex]
      • As [latex]z \rightarrow -1^{-}, r(z) \rightarrow \infty[/latex]
      • As [latex]z \rightarrow -1^{+}, r(z) \rightarrow -\infty[/latex]
    • Slant asymptote: [latex]y = z-2[/latex]
      • As [latex]z \rightarrow -\infty[/latex], the graph is above [latex]y=z-2[/latex]
      • As [latex]z \rightarrow \infty[/latex], the graph is below [latex]y=z-2[/latex]
    • The rectangular plane with a rational function that has a vertical asymptote at x=-1. The function has a slant asymptote.
      Answer to Exercise 11
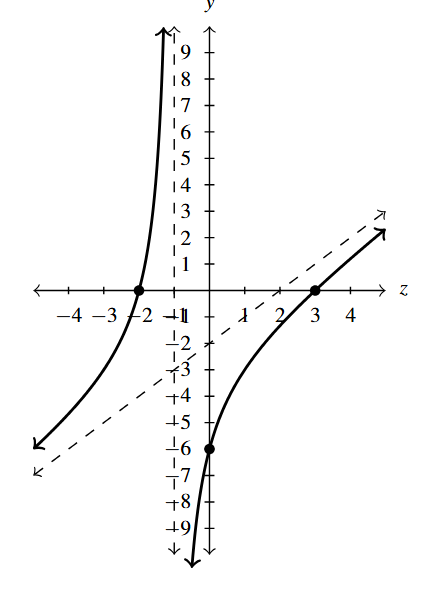
  12. [latex]r(z) = -z-2+\dfrac{6}{3-z} = \dfrac{z^2-z}{3-z}[/latex]
    • Domain: [latex](-\infty, 3) \cup (3, \infty)[/latex]
    • [latex]z[/latex]-intercepts: [latex](1,0)[/latex]
    • [latex]y[/latex]-intercept: None
    • Vertical asymptote: [latex]z = 3[/latex]
      • As [latex]z \rightarrow 3^{-}, r(z) \rightarrow \infty[/latex]
      • As [latex]z \rightarrow 3^{+}, r(z) \rightarrow -\infty[/latex]
    • Slant asymptote: [latex]y = -z-2[/latex]
      • As [latex]z \rightarrow -\infty[/latex], the graph is above [latex]y=-z-2[/latex]
      • As [latex]z \rightarrow \infty[/latex], the graph is below [latex]y=-z-2[/latex]
    • The rectangular plane with a rational function that has a vertical asymptote at x=3. The function has a slant asymptote.
      Answer to Exercise 12
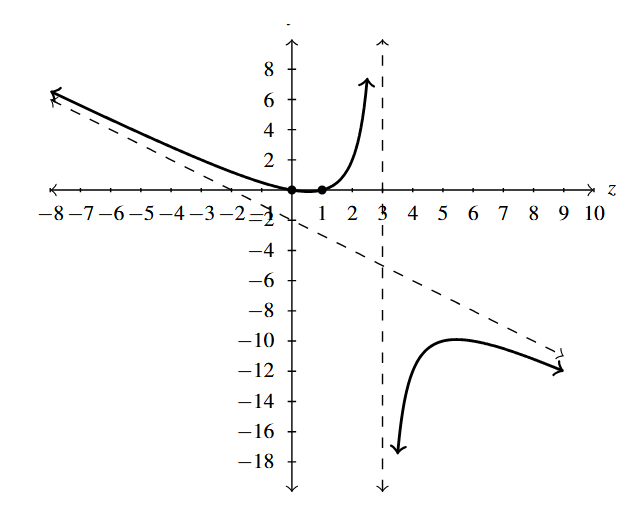
  13. [latex]f(x) = \dfrac{x^3+2x^2+x}{x^{2} -x-2} = \dfrac{x(x+1)}{x - 2}, \, x \neq -1[/latex]
    • Domain: [latex](-\infty, -1) \cup (-1, 2) \cup (2, \infty)[/latex]
    • [latex]x[/latex]-intercept: [latex](0,0)[/latex]
    • [latex]y[/latex]-intercept: [latex](0,0)[/latex]
    • Vertical asymptote: [latex]x = 2[/latex]
      • As [latex]x \rightarrow 2^{-}, f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow 2^{+}, f(x) \rightarrow \infty[/latex]
    • Hole at [latex](-1,0)[/latex]
    • Slant asymptote: [latex]y = x+3[/latex]
      • As [latex]x \rightarrow -\infty[/latex], the graph is below [latex]y=x+3[/latex]
      • As [latex]x \rightarrow \infty[/latex], the graph is above [latex]y=x+3[/latex]
    • The rectangular plane with a rational function that has a vertical asymptote at x=2. The function has a slant asymptote.
      Answer to Exercise 13
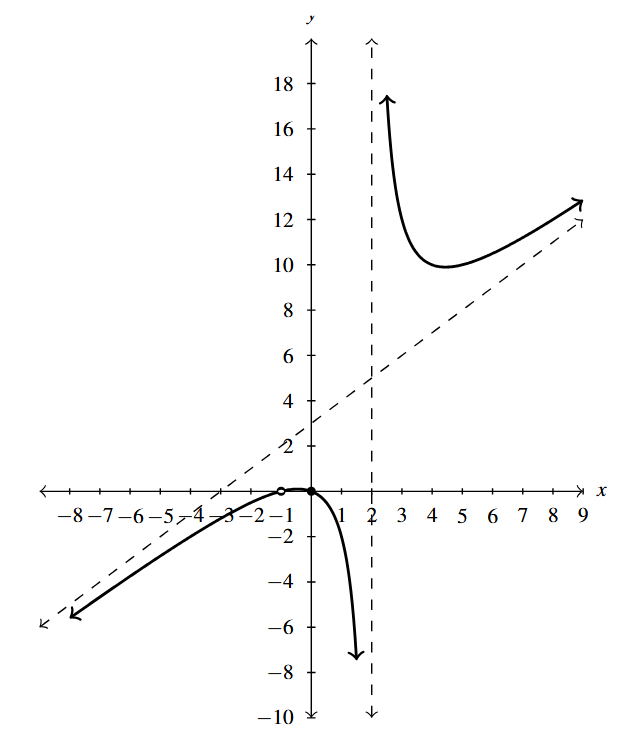
  14. [latex]f(x) = \dfrac{5x}{9-x^2} - x = \dfrac{x^{3} - 4x}{9-x^{2}} =\dfrac{x(x-2)(x+2)}{-(x-3)(x+3)}[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3, 3) \cup (3, \infty)[/latex]
    • [latex]x[/latex]-intercepts: [latex](-2, 0), (0, 0), (2, 0)[/latex]
    • [latex]y[/latex]-intercept: [latex](0, 0)[/latex]
    • Vertical asymptotes: [latex]x = -3, x = 3[/latex]
      • As [latex]x \rightarrow -3^{-}, \; f(x) \rightarrow \infty[/latex]
      • As [latex]x \rightarrow -3^{+}, \; f(x) \rightarrow -\infty[/latex]
      • As [latex]x \rightarrow 3^{-}, \; f(x) \rightarrow \infty[/latex]
      • As [latex]x \rightarrow 3^{+}, \; f(x) \rightarrow -\infty[/latex]
    • Slant asymptote: [latex]y = -x[/latex]
      • As [latex]x \rightarrow -\infty[/latex], the graph is above [latex]y=-x[/latex]
      • As [latex]x \rightarrow \infty[/latex], the graph is below [latex]y=-x[/latex]
    • The rectangular plane with a rational function that has two vertical asymptotes at x=-3 and x=3. The function has a slant asymptote.
      Answer to Exercise 14
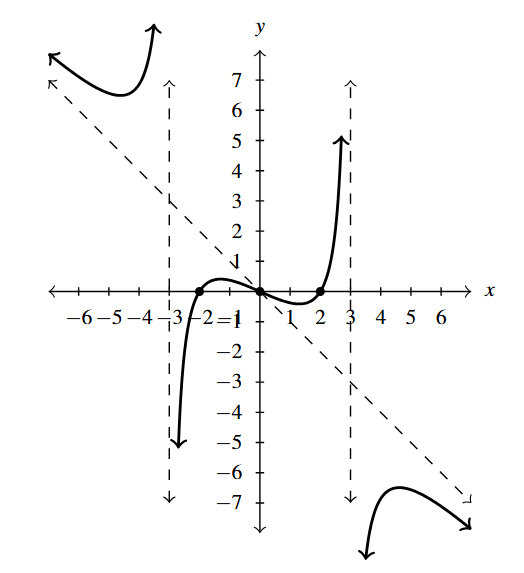
  15. [latex]g(t) = \dfrac{1}{2}t-1 + \dfrac{t+1}{t^2+1} = \dfrac{t(t^2-2t+3)}{2t^2+2}[/latex]
    • Domain: [latex](-\infty,\infty)[/latex]
    • [latex]t[/latex]-intercept: [latex](0,0)[/latex]
    • [latex]y[/latex]-intercept: [latex](0,0)[/latex]
    • Slant asymptote: [latex]y = \frac{1}{2}t-1[/latex]
      • As [latex]t \rightarrow -\infty[/latex], the graph is below [latex]y = \frac{1}{2}t-1[/latex]
      • As [latex]t \rightarrow \infty[/latex], the graph is above [latex]y = \frac{1}{2}t-1[/latex]
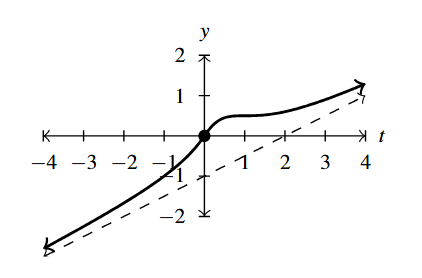
    • The rectangular plane with a rational function. The curve only has a slant asymptote and the curve is above the asymptote.
      Answer to Exercise 15
  16. [latex]g(t) = \dfrac{t^{2} - 2t + 1}{t^{3} + t^{2} - 2t}=\dfrac{t - 1}{t(t + 2)}, \; t \neq 1[/latex]
    • Domain: [latex](-\infty, -2) \cup (-2, 0) \cup (0, 1) \cup (1, \infty)[/latex]
    • No [latex]t[/latex]-intercepts
    • No [latex]y[/latex]-intercepts
    • Vertical asymptotes: [latex]t = -2[/latex] and [latex]t = 0[/latex]
      • As [latex]t \rightarrow -2^{-}, \; g(t) \rightarrow -\infty[/latex]
      • As [latex]t \rightarrow -2^{+}, \; g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow 0^{-}, \; g(t) \rightarrow \infty[/latex]
      • As [latex]t \rightarrow 0^{+}, \; g(t) \rightarrow -\infty[/latex]
    • Hole in the graph at [latex](1, 0)[/latex]
    • Horizontal asymptote: [latex]y = 0[/latex]
      • As [latex]t \rightarrow -\infty, \; g(t) \rightarrow 0^{-}[/latex]
      • As [latex]t \rightarrow \infty, \; g(t) \rightarrow 0^{+}[/latex]
    • The rectangular plane with a rational function that has two vertical asymptotes at x=-2 and x=0. The function has a hole at (1,0).
      Answer to Exercise 16
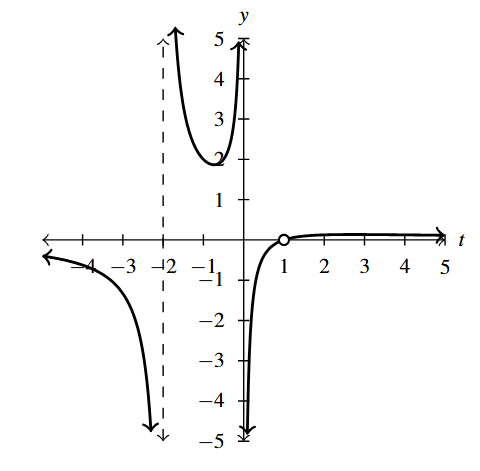
  17. [latex]f(x) = \dfrac{1}{x - 2}[/latex]
  18. [latex]F(x) = \dfrac{x-3}{(x-2)(x-3)} = \dfrac{x-3}{x^2-5x+6}[/latex]
  19. [latex]g(t) =\dfrac{t^2-1}{t}[/latex]
  20. [latex]G(t) = \dfrac{(t^2-1)(t+1)}{t(t+1)} = \dfrac{t^3+t^2-t-1}{t^2+t}[/latex]

Section 3.4 Answers

  1. [latex]x = -\dfrac{6}{7}[/latex]
  2. [latex]y = 1, 2[/latex]
  3. [latex]w = -1[/latex]
  4. [latex]x=-6, 2[/latex]
  5. No solution
  6. [latex]y = 0, \pm 2\sqrt{2}[/latex]
  7. [latex]w = -\sqrt{3}, -1[/latex]
  8. [latex]x = -\dfrac{3\sqrt{2}}{2}, \sqrt{2}[/latex]
  9. [latex]x = -\dfrac{\sqrt{3}}{2}, -\dfrac{\sqrt{3}}{4}[/latex]
  10. [latex]n = \dfrac{1}{2}[/latex]
  11. [latex]x = \dfrac{1 \pm \sqrt{5}}{2}, \dfrac{-1 \pm \sqrt{5}}{2}[/latex]
  12. [latex]t = -1[/latex]
  13. [latex]R = \pm \sqrt{\dfrac{0.08}{9.64 \pi}}[/latex]
  14. [latex]x = -\dfrac{231}{400} \approx -0.58[/latex], [latex]x = \dfrac{77}{200}[/latex]
  15. [latex]c = \pm \sqrt{\dfrac{4 \cdot 6.75 \times 10^{16}}{3}} = \pm 3.00 \times 10^{8}[/latex]
  16. [latex]y = \dfrac{1 - 3x}{x+2}[/latex], [latex]y \neq -3[/latex], [latex]x \neq -2[/latex]
  17. [latex]y = \dfrac{x-1}{x-3}[/latex], [latex]y \neq 1[/latex], [latex]x \neq 3[/latex]
  18. [latex]T_{\text{\tiny 2}} = \dfrac{V_{\text{\tiny 2}}T_{\text{\tiny 1}}}{V_{\text{\tiny 1}}}[/latex], [latex]T_{\text{\tiny 1}} \neq 0, T_{\text{\tiny 2}} \neq 0, V_{\text{\tiny 1}} \neq 0[/latex]
  19. [latex]t_{\text{\tiny 0}} = \dfrac{2}{2t_{\text{\tiny 1}} + 1}[/latex], [latex]t_{\text{\tiny 1}} \neq -\dfrac{1}{2}[/latex]
  20. [latex]x = \dfrac{1 \pm \sqrt{25v_{r}^2+1}}{5}[/latex], [latex]x \neq \pm v_{r}[/latex]
  21. [latex]R= \dfrac{-(8P-25) \pm \sqrt{(8P-25)^2 - 64P^2}}{2P} = \dfrac{(25-8P) \pm 5 \sqrt{25-16P}}{2P}[/latex], [latex]P \neq 0[/latex], [latex]R \neq -4[/latex]

 

  1. This is hard to see on the calculator, but trust us, the graph is below the [latex]t[/latex]-axis to the left of [latex]t = -7[/latex]. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Functions, Trigonometry, and Systems of Equations (Second Edition) Copyright © 2025 by Texas A&M Mathematics Department is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book