"

Section 4.1 Answers

  1. [latex]F(x) = \sqrt{x+3}-2[/latex]
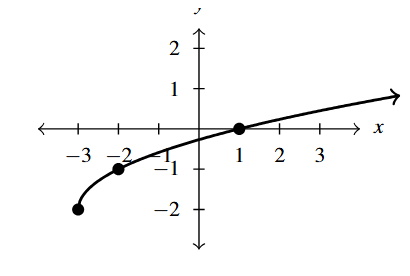
    The rectangular plane with a curve that starts at (-3,-2) and increases through (1,0).
    Answer to Exercise 1
  2. [latex]F(x) = \sqrt{4-x}-1 = \sqrt{-x+4} - 1[/latex]
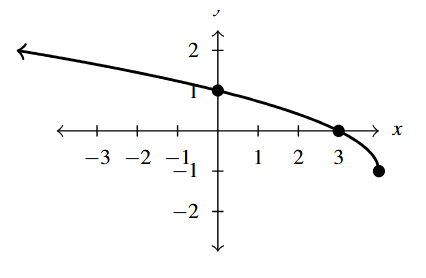
    The rectangular plane with the curve that decreases through (0,1) and ends at (4,-1).
    Answer to Exercise 2
  3. [latex]F(x) = \sqrt[3]{x-1}-2[/latex].
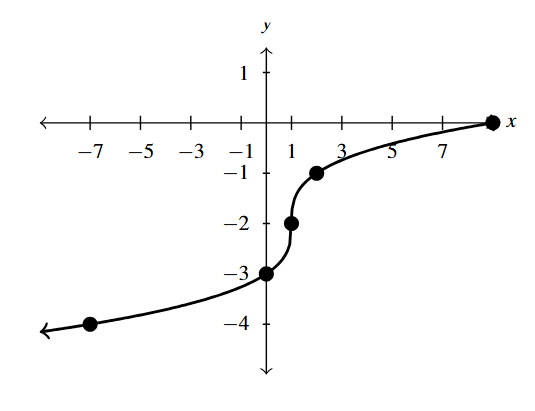
    The rectangular plane with a curve that increases through the points (0,-3) and (9,0).
    Answer to Exercise 3
  4. [latex]F(x) = -\sqrt[3]{8x + 8} + 4[/latex]
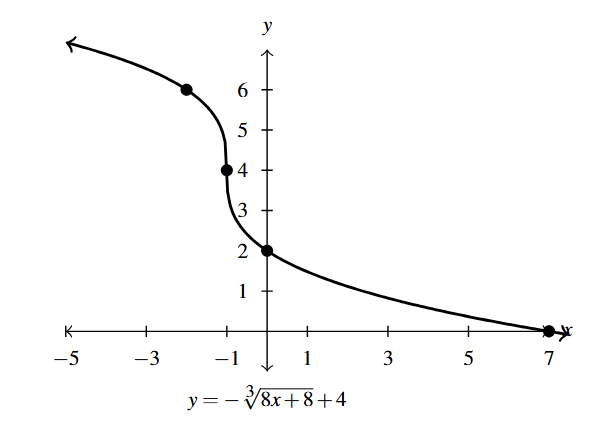
    The rectangular plane with a curve that decreases through (-2,6) and (0,2).
    Answer to Exercise 4
  5. [latex]F(x) = \sqrt[4]{x-1}-2[/latex]
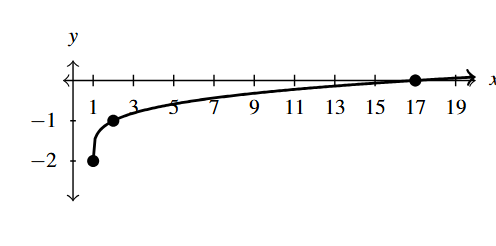
    The rectangular plane with a curve that starts at (1,-2) that increases through (17,0).
    Answer to Exercise 5
  6. [latex]F(x) = -3\sqrt[4]{x - 7} +1[/latex]
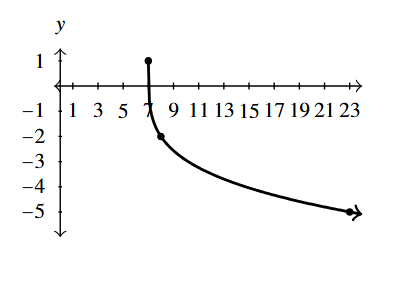
    The rectangular plane with a curve that starts at (7,1) and decreases through (8,-2).
    Answer to Exercise 6
  7. [latex]F(x) = \sqrt[5]{x + 2} + 3[/latex]
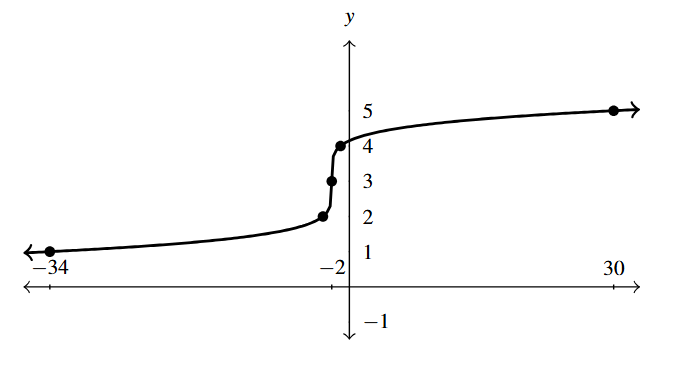
    The rectangular plane with a curve that increases through the points (-32,1) and (30,5).
    Answer to Exercise 7
  8. [latex]F(x) = \sqrt[8]{-x} - 2[/latex]
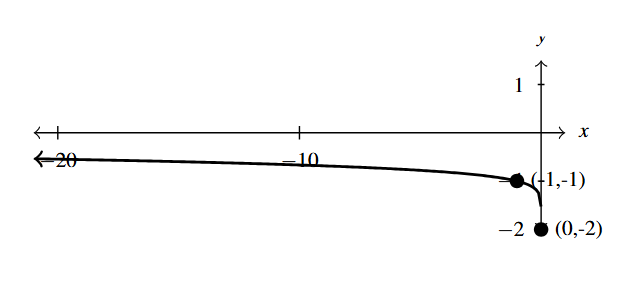
    The rectangular plane with a curve that decreases through (-1,-1) and stops at (0,-2).
    Answer to Exercise 8
  9. One solution is: [latex]F(x) = -\sqrt{x+4}+2[/latex]
  10. One solution is: [latex]F(x) =2\sqrt{-x+1}[/latex]
  11. One solution is: [latex]F(x) = -\sqrt[3]{2x+1}[/latex]
  12. One solution is: [latex]F(x) =2\sqrt[3]{x-1}-2[/latex]
  13. .
    1. [latex](-\infty, 4][/latex]
    2. [latex](-2, \infty)[/latex]
    3. [latex]\left[ \frac{1}{2}, \infty \right)[/latex]
    4. [latex][-2,2][/latex]
    5. [latex](-\infty, -2) \cup (2, \infty)[/latex]
    6. [latex](-\infty, -2] \cup [1, \infty)[/latex]
  14. [latex]f(x) = \sqrt{1 - x^2}[/latex]
    • Domain: [latex][-1, 1][/latex]
    • Intercepts: [latex](-1,0)[/latex], [latex](1,0)[/latex]
    • Graph:
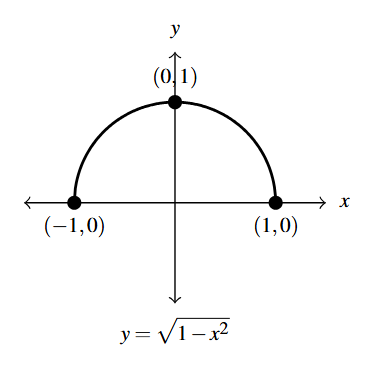
      The rectangular plane with a curve that starts at (-1,0), goes through (0,1) and ends at (1,0).
      Graph Answer to Exercise 14
    • Range: [latex][0,1][/latex]
    • Local maximum: [latex](0,1)[/latex]
    • Increasing: [latex][-1,0][/latex], Decreasing: [latex][0,1][/latex]
    • Unusual steepness[1] at [latex]x = -1[/latex] and [latex]x = 1[/latex]
    • Sign Diagram:
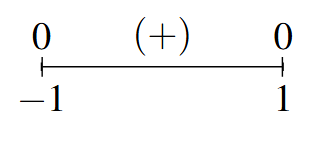
      A number line that starts at x=-1 and ends at x=1 with 0 above each. The interval between has a (+).
      Sign Diagram Answer to Exercise 14
    • Note: [latex]f[/latex] is even.
  15. [latex]f(x) = \sqrt{x^2-1}[/latex]
    • Domain: [latex](-\infty, -1] \cup [1,\infty)[/latex]
    • Intercepts: [latex](-1,0)[/latex], [latex](1,0)[/latex]
    • Graph:
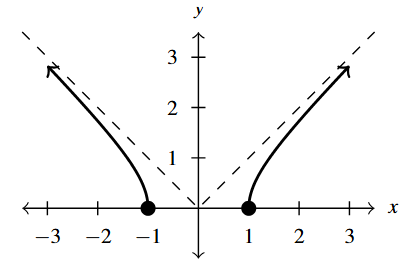
      The rectangular plane with a curve that decreases to (-1,0) and then starts back at (1,0) and increases.
      Graph Answer to Exercise 15
    • As [latex]x \rightarrow \pm \infty[/latex], [latex]f(x) \rightarrow \infty[/latex]
    • Range: [latex][0, \infty)[/latex]
    • Increasing: [latex][1, \infty)[/latex]
    • Decreasing: [latex](-\infty, -1][/latex]
    • Unusual steepness[2]at [latex]x = -1[/latex] and [latex]x = 1[/latex]
    • Using Calculus, one can show [latex]y = \pm x[/latex] are slant asymptotes to the graph.
    • Sign Diagram:
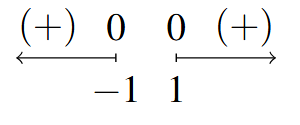
      A number line broken into two parts. The left side stops at negative -1 and the right side starts at 1. There is a 0 above negative 1 and 1. The left side has a (+), while the right side has (+).
      Sign Diagram Answer to Exercise 15
    • Note: [latex]f[/latex] is even.
  16. [latex]g(t) = t\sqrt{1-t^2}[/latex]
    • Domain: [latex][-1,1][/latex]
    • Intercepts: [latex](-1,0)[/latex], [latex](0,0)[/latex], [latex](1,0)[/latex]
    • Graph:
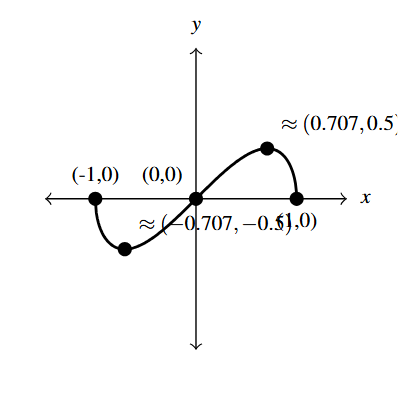
      The rectangular plane with a curve that starts at (-1,0) and decreases to approximately (-0.707, -0.5). The graph then increases to approximately (0.707, 0.5) and then decreases to the end at (1,0).
      Graph Answer to Exercise 16
    • Range: [latex]\approx [-0.5, 0.5][/latex]
    • Local minimum [latex]\approx (-0.707, -0.5)[/latex]
    • Local maximum: [latex]\approx (0.707, 0.5)[/latex]
    • Increasing: [latex]\approx [-0.707, 0.707][/latex]
    • Decreasing: [latex]\approx [-1, -0.707][/latex], [latex][0.707, 1][/latex]
    • Unusual steepness at [latex]t = -1[/latex] and [latex]t = 1[/latex]
    • Sign Diagram:
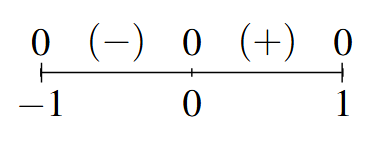
      A number line that starts at x=-1 and ends at x=1. The line includes x=0. All three values of x have a 0 above. The first interval has a (-) and the second is (+).
      Sign Diagram Answer to Exercise 16
    • Note: [latex]g[/latex] is odd.
  17. [latex]g(t) = t\sqrt{t^2-1}[/latex]
    • Domain: [latex](-\infty, -1] \cup [1,\infty)[/latex]
    • Intercepts: [latex](-1,0)[/latex], [latex](1,0)[/latex]
    • Graph:
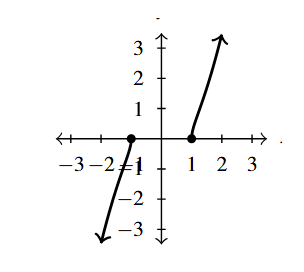
      The rectangular plane with a curve that increases to (-1,0) and then starts up again at (1,0) and continues increasing.
      Graph Answer to Exercise 17
    • As [latex]t \rightarrow -\infty[/latex], [latex]g(t) \rightarrow -\infty[/latex]
    • As [latex]t \rightarrow \infty[/latex], [latex]g(t) \rightarrow \infty[/latex]
    • Range: [latex](-\infty, \infty)[/latex]
    • Increasing: [latex](-\infty, -1][/latex], [latex][1, \infty)[/latex]
    • Unusual steepness at [latex]t = -1[/latex] and [latex]t = 1[/latex]
    • Sign Diagram:
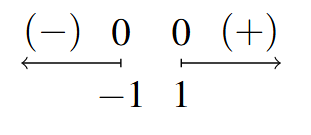
      A number line broken into two parts. The left side stops at negative -1 and the right side starts at 1. There is a 0 above negative 1 and 1. The left side has a (-), while the right side has (+).
      Sign Diagram Answer to Exercise 17
    • [latex]g[/latex] is odd.
  18. [latex]f(x) = \sqrt[4]{\dfrac{16x}{x^2 - 9}}[/latex]
    • Domain: [latex](-3, 0] \cup (3, \infty)[/latex]
    • Intercept: [latex](0,0)[/latex]
    • Graph:
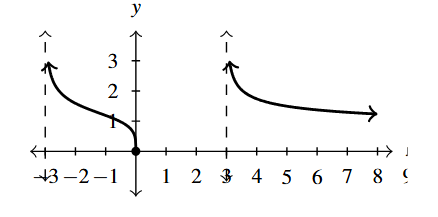
      The rectangular plane with a curve that decreases from a vertical asymptote at x = -3 to the point (0,0). The curve picks up again after another vertical asymptote at x =3 and decreases to the right.
      Graph Answer to Exercise 18
    • As [latex]x \rightarrow \infty[/latex], [latex]f(x) \rightarrow 0[/latex]
    • Range: [latex][0, \infty)[/latex]
    • Decreasing: [latex](-3, 0][/latex], [latex](3, \infty)[/latex]
    • Unusual steepness at [latex]x = 0[/latex]
    • Vertical asymptotes: [latex]x = -3[/latex] and [latex]x = 3[/latex]
    • Horizontal asymptote: [latex]y = 0[/latex]
    • Sign Diagram:
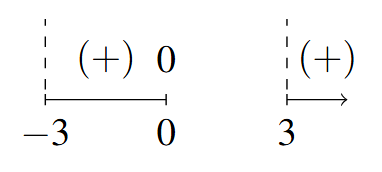
      A number line that starts at x=-3 with a dashed line, ends at x=0 and has a 0 above. The number line starts up again at x=3 with a dashed line. The first interval has a (+) and the second has a (+).
      Sign Diagram Answer to Exercise 18
  19. [latex]f(x) = \dfrac{5x}{\sqrt[3]{x^{3} + 8}}[/latex]
    • Graph:
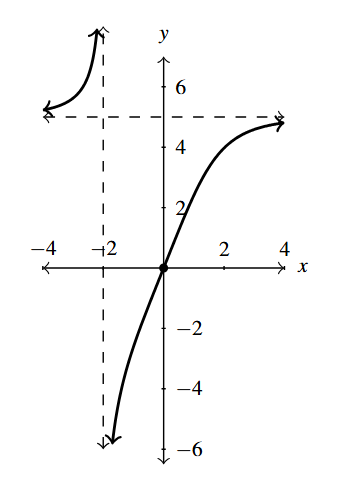
      The rectangular plane with a curve that has a vertical asymptote at x=-2 and a horizontal asymptote to y=5.
      Graph Answer to Exercise 19
    • Domain: [latex](-\infty, -2) \cup (-2, \infty)[/latex]
    • Intercept: [latex](0,0)[/latex]
    • As [latex]x \rightarrow \pm \infty[/latex], [latex]f(x) \rightarrow 5[/latex]
    • Range: [latex](-\infty, 5) \cup (5, \infty)[/latex]
    • Increasing: [latex](-\infty, -2)[/latex], [latex](-2, \infty)[/latex]
    • Vertical asymptote [latex]x = -2[/latex]
    • Horizontal asymptote [latex]y = 5[/latex]
    • Sign Diagram:
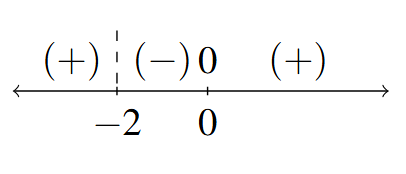
      A number line with a dashed line at x=2 and a 0 at x=0. The signs: (+), (-), and (+) are in the respective intervals between the given values of x as we move left to right on the number line.
      Sign Diagram Answer to Exercise 19
  20. [latex]g(t) = \sqrt{t(t + 5)(t - 4)}[/latex]
    • Domain: [latex][-5, 0] \cup [4, \infty)[/latex]
    • Intercepts [latex](-5,0)[/latex], [latex](0,0)[/latex], [latex](4,0)[/latex]
    • As [latex]t \rightarrow \infty[/latex], [latex]g(t) \rightarrow \infty[/latex]
    • Graph:
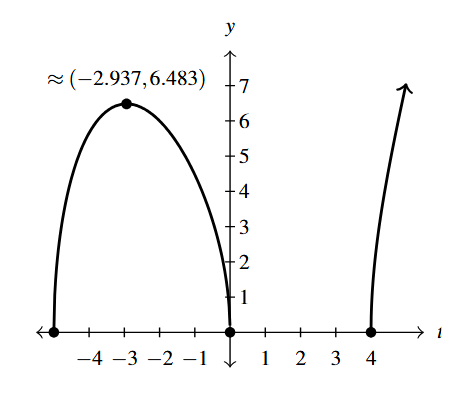
      The rectangular plane with a curve starts at (-5,0) and increases to (-2.937, 6.483) and decreasing to (0,0). The graph starts again at (4,0) and increases from there.
      Graph Answer to Exercise 20
    • Range: [latex][0, \infty)[/latex]
    • Local maximum [latex]\approx (-2.937, 6.483)[/latex]
    • Increasing: [latex]\approx [-5, -2.937][/latex], [latex][4, \infty)[/latex]
    • Decreasing: [latex]\approx [-2.937,0][/latex]
    • Unusual steepness at [latex]t = -5, t = 0[/latex] and [latex]t = 4[/latex]
    • Sign Diagram:
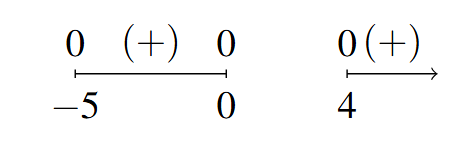
      A number line that starts at x = -5 and goes to x = 0, then starts up again at x=4. There are 0's above each x. The first interval has a (+) and the second interval has a (+).
      Sign Diagram Answer to Exercise 20
  21. [latex]g(t) = \sqrt[3]{t^{3} + 3t^{2} - 6t - 8}[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Intercepts: [latex](-4,0)[/latex], [latex](-1,0)[/latex], [latex](0,-2)[/latex], [latex](2,0)[/latex]
    • Graph:
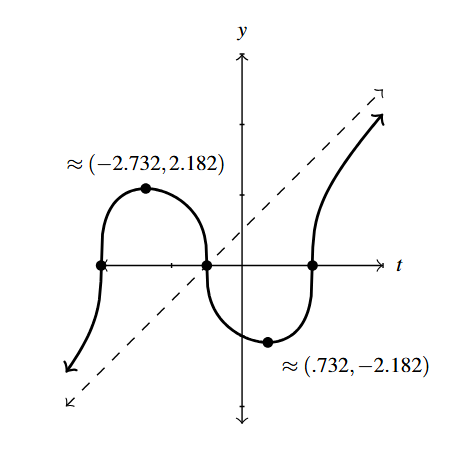
      The rectangular plane with a curve that approaches a slant asymptote and goes through the points (-2.732, 2.182) and (0.732, -2.182).
      Graph Answer to Exercise 21
    • As [latex]t \rightarrow -\infty[/latex], [latex]g(t) \rightarrow -\infty[/latex]
    • As [latex]t \rightarrow \infty[/latex], [latex]g(t) \rightarrow \infty[/latex]
    • Range: [latex](-\infty, \infty)[/latex]
    • Local maximum: [latex]\approx (-2.732, 2.182)[/latex]
    • Local minimum: [latex]\approx (0.732, -2.182)[/latex]
    • Increasing: [latex]\approx (-\infty, -2.732][/latex], [latex][0.732, \infty)[/latex]
    • Decreasing: [latex]\approx [-2.732, 0.732][/latex]
    • Unusual steepness at [latex]t = -4, t = -1[/latex] and [latex]t = 2[/latex]
    • Using Calculus it can be shown that [latex]y = t + 1[/latex] is a slant asymptote of this graph.
    • Sign Diagram:
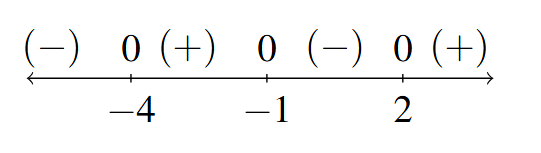
      A number line with x=-4, x=-1, and x=2 with 0 above each. The signs: (-), (+), (-), and (+) are in the respective intervals between the given values of x as we move left to right on the number line.
      Sign Diagram Answer to Exercise 21
  22. [latex]C(x) = 15x+20\sqrt{100+(30-x)^2}[/latex], [latex]0 \leq x \leq 30[/latex]. The calculator gives the absolute minimum at approximately [latex](18.66, 582.29)[/latex]. This means to minimize the cost, approximately 18.66 miles of cable should be run along Route 117 before turning off the road and heading towards the outpost. The minimum cost to run the cable is approximately \$582.29.
  23. .
    1. [latex]h(r) = \frac{300}{\pi r^2}[/latex], [latex]r > 0[/latex]
    2. [latex]S(r) = \pi r \sqrt{r^2+\left(\frac{300}{\pi r^2}\right)^2} = \frac{\sqrt{\pi^2 r^6+90000}}{r}[/latex], [latex]r>0[/latex]
    3. The calculator gives the absolute minimum at the point [latex]\approx (4.07, 90.23)[/latex]. This means the radius should be (approximately) 4.07 centimeters and the height should be 5.76 centimeters to give a minimum surface area of 90.23 square centimeters.
  24. [latex]9.8 \left(\dfrac{1}{4\pi}\right)^{2} \approx 0.062[/latex] meters or 6.2 centimeters
  25. .
    1. [latex][0, c)[/latex]
    2. [latex]\begin{array}{ll} m(.1c) = \dfrac{m_{r}}{\sqrt{.99}} \approx 1.005m_{r} & m(.5c) = \dfrac{m_{r}}{\sqrt{.75}} \approx 1.155m_{r} \\ & \\ m(.9c) = \dfrac{m_{r}}{\sqrt{.19}} \approx 2.294m_{r} & m(.999c) = \dfrac{m_{r}}{\sqrt{.0.001999}} \approx 22.366m_{r} \\ \end{array}[/latex]
    3. As [latex]v \rightarrow c^{-}, \, m(x) \rightarrow \infty[/latex]
    4. If the object is traveling no faster than approximately 0.99995 times the speed of light, then its observed mass will be no greater than [latex]100m_{r}[/latex].
  26. [latex]k^{-1}(x) = \dfrac{x}{\sqrt{x^{2} - 4}}[/latex]

Section 4.2 Answers

  1. [latex]F(x) = (x-2)^{\frac{2}{3}}-1[/latex]
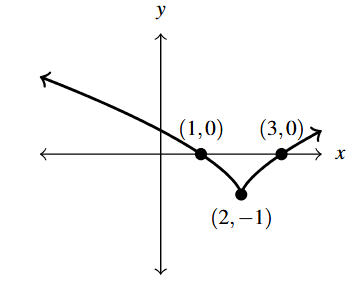
    The rectangular plane with a curve that decreases through (1,0) to (2,-1) and then sharply turns and increase through (3,0).
    Answer to Exercise 1
  2. [latex]G(t) = (t+3)^{\pi} +1[/latex]
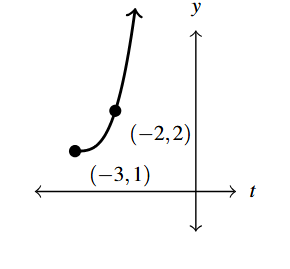
    The rectangular plane with a curve that starts at (-3,1) and increases through (-2,2).
    Answer to Exercise 2
  3. [latex]F(x) = 3-x^{\frac{2}{3}} = (-1)x^{\frac{2}{3}} + 3[/latex]
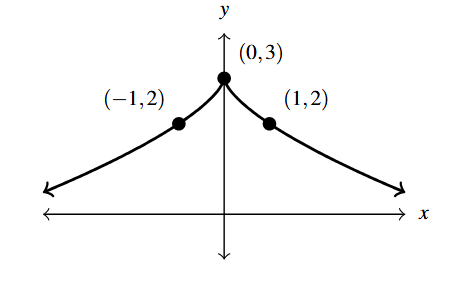
    The rectangular plane with a curve that increases through (-1,2) to (0,3) and then sharply turns and decrease through (1,2).
    Answer to Exercise 3
  4. [latex]G(t) = (1-t)^{\pi}-2 = ((-1)t+1)^{\pi}-2[/latex]
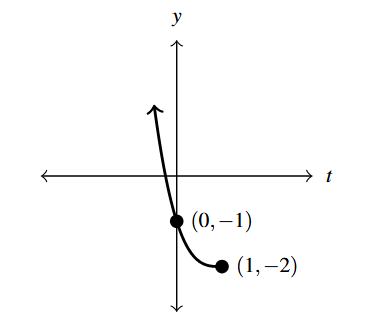
    The rectangular plane with a curve that decreases through (0,-1) an stops at (1,-2).
    Answer to Exercise 4
  5. [latex]F(x) =(2x+5)^{\frac{2}{3}}+1[/latex]
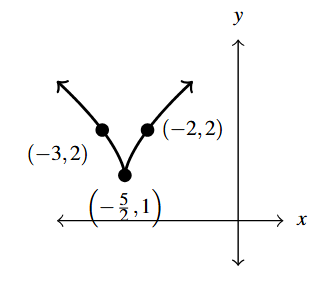
    The rectangular plane with a curve that decreases through (-3,2) to (-2.5,1) and then sharply turns and increase through (-2,2).
    Answer to Exercise 5
  6. [latex]G(t) = \left( \dfrac{t+3}{2}\right)^{\pi}-1= \left( \frac{1}{2} \, t + \frac{3}{2}\right)^{\pi} -1[/latex]
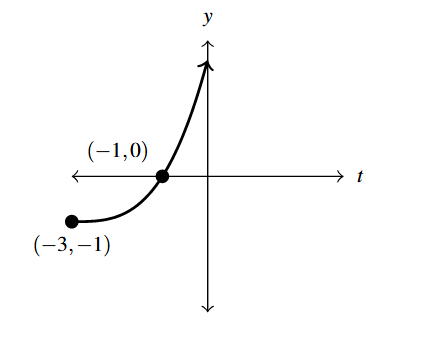
    The rectangular plane with a curve that starts at (-3,-1) and increases through (-1,0).
    Answer to Exercise 6
  7. One solution is: [latex]F(x) = 2(x-1)^{\frac{2}{3}}-2[/latex]
  8. One solution is: [latex]F(x) =-(x+1)^{\frac{2}{3}} + 4[/latex]
  9. [latex]f(x) = x^{\frac{2}{3}}(x - 7)^{\frac{1}{3}}[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Intercepts: [latex](0,0)[/latex], [latex](7,0)[/latex]
    • Graph:
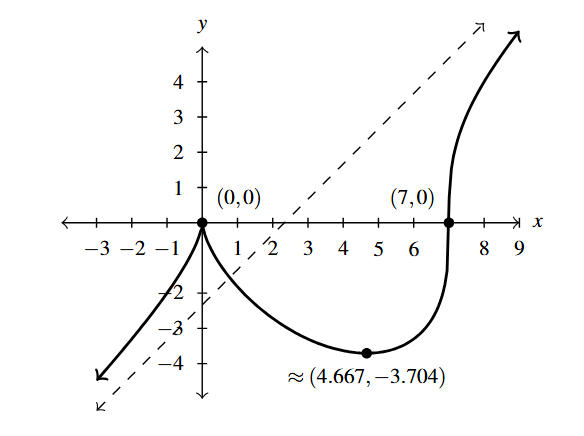
      The rectangular plane with the curve with a slant asymptote.
      Graph Answer to Exercise 9
    • As [latex]x \rightarrow -\infty[/latex], [latex]f(x) \rightarrow -\infty[/latex]
    • As [latex]x \rightarrow \infty[/latex], [latex]f(x) \rightarrow \infty[/latex]
    • Range: [latex](-\infty, \infty)[/latex]
    • Local minimum: [latex]\approx (4.667, -3.704)[/latex]
    • Local maximum: [latex](0,0)[/latex] (this is a cusp)
    • Increasing: [latex](-\infty, 0][/latex], [latex]\approx [4.667, \infty)[/latex]
    • Decreasing: [latex][0, 4.667][/latex]
    • Unusual steepness at [latex]x = 7[/latex]
    • Using Calculus it can be shown that [latex]y = x - \frac{7}{3}[/latex] is a slant asymptote of this graph.
    • Sign Diagram:
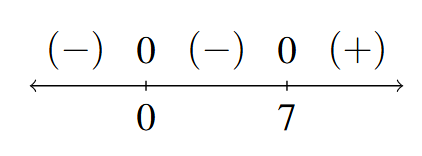
      A number line with x=0 and x=7 marked with a 0 above them. The signs: (-), (-), and (+) are in the respective intervals between the given values of x as we move left to right on the number line.
      Sign Diagram Answer to Exercise 9
  10. [latex]f(x) = x^{\frac{3}{2}}(x - 7)^{\frac{1}{3}}[/latex]
    • Domain: [latex][0, \infty)[/latex]
    • Intercepts: [latex](0,0)[/latex], [latex](7,0)[/latex]
    • Graph:
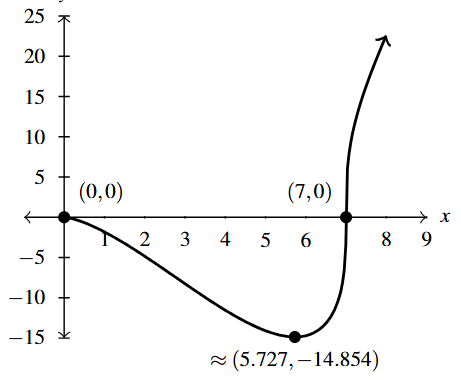
      The rectangular plane with the curve that starts at (0,0) decreases to the minimum and then increases.
      Graph Answer to Exercise 10
    • As [latex]x \rightarrow \infty[/latex], [latex]f(x) \rightarrow \infty[/latex]
    • Range: [latex]\approx [-14.854, \infty)[/latex]
    • Local minimum: [latex]\approx (5.727, -14.854)[/latex]
    • Increasing: [latex]\approx [5.727, \infty)[/latex]
    • Decreasing: [latex]\approx [0, 5.727][/latex]
    • Unusual steepness at [latex]x = 7[/latex]
    • Sign Diagram:
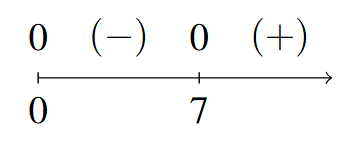
      A number line starts at x=0 increases to the right with x=7 marked with a 0 above them. The signs: (-), and (+) are in the respective intervals between the given values of x as we move left to right on the number line.
      Sign Diagram Answer to Exercise 10
  11. [latex]g(t) = 2t(t+3)^{-\frac{1}{3}}[/latex]
    • Domain: [latex](-\infty, -3) \cup (-3, \infty)[/latex]
    • Intercept: [latex](0,0)[/latex]
    • Graph:
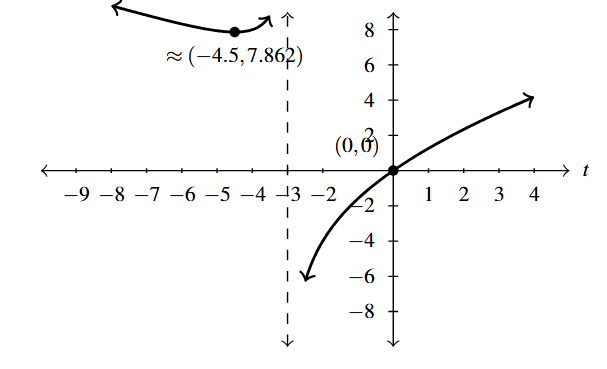
      The rectangular plane with a curve that has a vertical asymptote at x=-3.
      Graph Answer to Exercise 11
    • As [latex]t \rightarrow \pm \infty[/latex], [latex]g(t) \rightarrow \infty[/latex]
    • Range: [latex](-\infty, \infty)[/latex]
    • Local minimum: [latex]\approx (-4.5, 7.862)[/latex]
    • Increasing: [latex]\approx [-4.5, -3)[/latex], [latex](-3,\infty)[/latex]
    • Decreasing: [latex]\approx (-\infty, -4.5][/latex]
    • Vertical Asymptote: [latex]t = -3[/latex]
    • Sign Diagram:
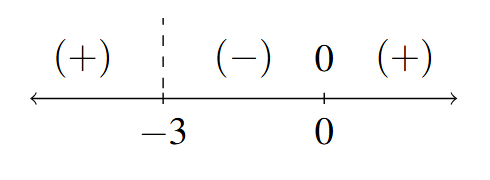
      A number line with a dashed line above x=-3 and x=7 marked with a 0 above it. The signs: (+), (-), and (+) are in the respective intervals between the given values of x as we move left to right on the number line.
      Sign Diagram Answer to Exercise 11
  12. [latex]g(t)= t^{\frac{3}{2}}(t-2)^{-\frac{1}{2}}[/latex]
    • Domain: [latex](2, \infty)[/latex]
    • Graph:
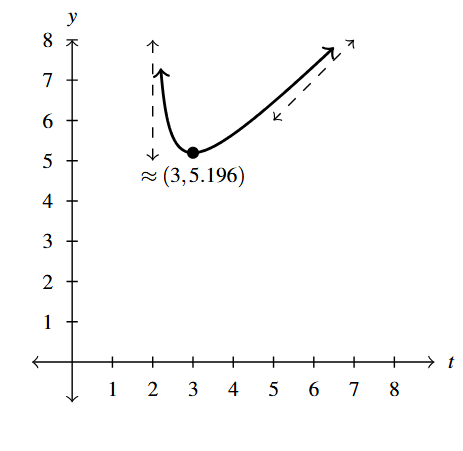
      The rectangular plane with a curve between the vertical asymptote t=2 and a slant asymptote y=t+1.
      Graph Answer to Exercise 12
    • As [latex]t \rightarrow \infty[/latex], [latex]g(t) \rightarrow \infty[/latex]
    • Range: [latex]\approx [5.196, \infty)[/latex]
    • Local minimum: [latex]\approx (3, 5.196)[/latex]
    • Increasing: [latex]\approx [3, \infty)[/latex]
    • Decreasing: [latex]\approx (2,3][/latex]
    • Vertical asymptote: [latex]t = 2[/latex]
    • Using Calculus it can be shown that [latex]y = t+1[/latex] is a slant asymptote of this graph.
    • Sign Diagram:
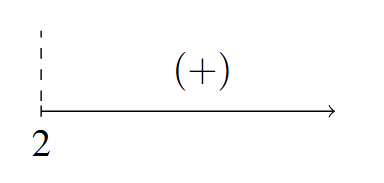
      A number line starts with a dashed line at x=2. The sign above the interval is (+).
      Sign Diagram Answer to Exercise 12
  13. [latex]f(x) = x^{0.4}(3-x)^{0.6}[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Intercepts: [latex](0,0)[/latex], [latex](3,0)[/latex]
    • Graph:
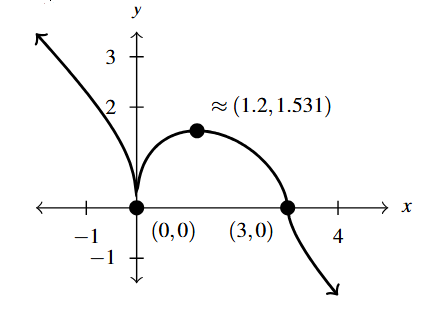
      The rectangular plane with a curve f(x).
      Graph Answer to Exercise 13
    • As [latex]x \rightarrow -\infty[/latex], [latex]f(x) \rightarrow \infty[/latex]
    • As [latex]x \rightarrow \infty[/latex], [latex]f(x) \rightarrow -\infty[/latex]
    • Range: [latex](-\infty, \infty)[/latex]
    • Local minimum: [latex](0,0)[/latex] (this is a cusp)
    • Local maximum: [latex]\approx (1.2, 1.531)[/latex]
    • Increasing: [latex]\approx [0, 1.2][/latex]
    • Decreasing: [latex]\approx (-\infty, 0][/latex], [latex][1.2, \infty)[/latex]
    • Unusual Steepness: [latex]x = 3[/latex]
    • Sign Diagram:
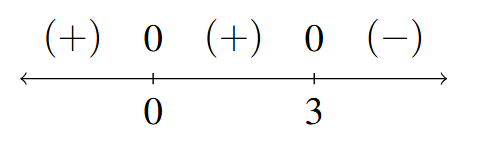
      A number line with x=0 and x=3 marked with a 0 above them. The signs: (+), (+), and (-) are in the respective intervals between the given values of x as we move left to right on the number line.
      Sign Diagram Answer to Exercise 13
  14. [latex]f(x) = x^{0.5}(3-x)^{0.5}[/latex]
    • Domain: [latex][0,3][/latex]
    • Intercepts: [latex](0,0)[/latex], [latex](3,0)[/latex]
    • Graph:
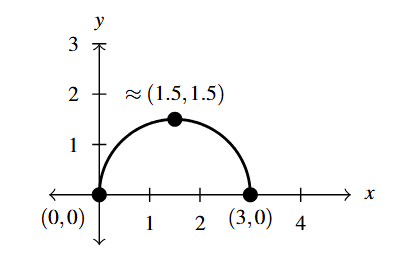
      The rectangular plane with a curve that starts at (0,0) increases to (1.5,1.5) and decreases to the stop at (3,0).
      Graph Answer to Exercise 14
    • Range: [latex]\approx [0, 1.5][/latex]
    • Increasing: [latex]\approx [0, 1.5][/latex]
    • Decreasing: [latex]\approx [1.5, 3][/latex]
    • Unusual Steepness:[3] [latex]x=0[/latex], [latex]x = 3[/latex]
    • Sign Diagram:
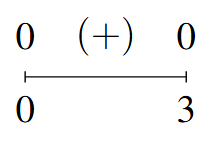
      A number line that starts at x=0 and ends at x=3 with 0 above them. The sign above the interval (+).
      Sign Diagram Answer to Exercise 14
  15. [latex]g(t) = 4t (9-t^2)^{-\sqrt{2}}[/latex]
    • Domain: [latex](-3, 3)[/latex]
    • Intercepts: [latex](0,0)[/latex]
    • Graph:
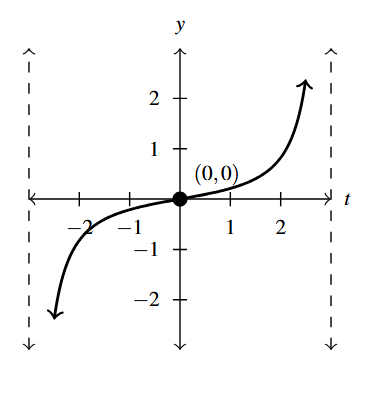
      The rectangular plane with a curve between the vertical asymptotes x = -3 and x= 3.
      Graph Answer to Exercise 15
    • Range: [latex](-\infty, \infty)[/latex]
    • Increasing: [latex](-3,3)[/latex]
    • Sign Diagram:
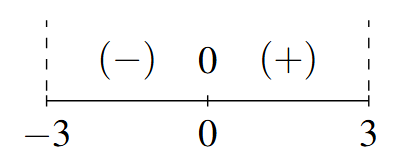
      A number line start at x=-3 and stop at x=3 with dashed lines. The x=0 is also marked with a 0 above. The signs: (-) and (+) are in the respective intervals between the given values of x as we move left to right on the number line.
      Sign Diagram Answer to Exercise 15
    • Note: [latex]g[/latex] is odd
  16. [latex]g(t) = 3(t^2+1)^{-\pi}[/latex]
    • Domain: [latex](-\infty, \infty)[/latex]
    • Intercept: [latex](0,3)[/latex]
    • Graph:
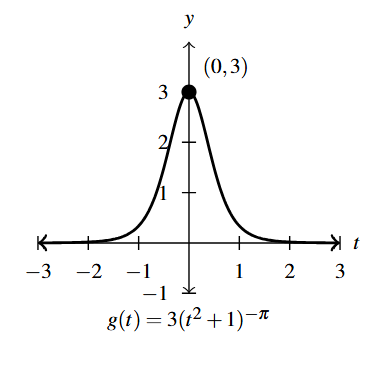
      The rectangular plane with a curve above the y-axis.
      Graph Answer to Exercise 16
    • As [latex]t \rightarrow \pm \infty[/latex], [latex]g(t) \rightarrow 0[/latex]
    • Range: [latex](0, 3][/latex]
    • Increasing: [latex](-\infty, 0][/latex]
    • Decreasing: [latex][0, \infty)[/latex]
    • Horizontal asymptote: [latex]y =0[/latex]
    • Sign Diagram:
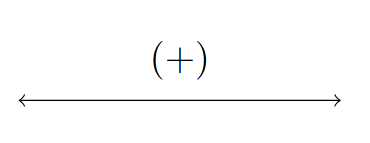
      A number line with a (+) above.
      Sign Diagram Answer to Exercise 16
    • Note: [latex]g[/latex] is even
  17. As in Exercise 51 in Section 2.2 and Exercise 22 in Section 3.2, the slopes of these curves near [latex]x=1[/latex] approach the value of the exponent on [latex]x.[/latex]
    A table with five rows and five columns. The first row is the header row: f(x), [0.9,1.1], [0.99, 1.01], [0.999, 1.001], and [0.9999, 1.0001]. The first column has the function values x raised to the one-half, x raised to the two-third, x raised to the negative 0.23, and x raised to the pi. The table is filled in.
    Answer to Exercise 17
  18. .
    1. [latex]W \approx 37.55^{\circ}[/latex]F
    2. [latex]V \approx 9.84[/latex] miles per hour

Section 4.3 Answers

  1. [latex]x=3[/latex]
  2. [latex]x = \frac{1}{4}[/latex]
  3. [latex]t=-3[/latex]
  4. [latex]t = -\frac{1}{3}, \; \frac{2}{3}[/latex]
  5. [latex]x = \frac{1}{4}[/latex]
  6. [latex]x = \frac{\sqrt{3}}{2}[/latex]
  7. [latex]t = \pm 8[/latex]
  8. [latex]t = 6[/latex]
  9. [latex]x = 4[/latex]
  10. [latex]x=-2, 6[/latex]
  11. [latex]t=-8, \frac{27}{8}[/latex]
  12. [latex]t=-1, \frac{1}{27}[/latex]
  13. [latex]x=16[/latex]
  14. [latex]x = \frac{1}{81}, \frac{1}{16}[/latex]
  15. [latex]K=f(L) = (240)^{ \frac{5}{3}} L^{- \frac{2}{3}}[/latex]. [latex]f(100) \approx 430.2148[/latex]. This means in order for the production level of Sasquatchia to reach 300,000 Bigfoot Bullion with a labor investment of 100,000 hours, the country needs to invest approximately 430 Bigfoot Bullion into capital.

Section 4.4 Answers

  1. [latex](-\infty, -3] \cup [1, \infty)[/latex]
  2. [latex]\left(-\infty, -\frac{1}{4}\right) \cup \left(-\frac{1}{4}, \infty \right)[/latex]
  3. No solution
  4. [latex](-\infty, \infty)[/latex]
  5. [latex]\left\{2 \right\}[/latex]
  6. No solution
  7. [latex]\left[-\frac{1}{3}, 4 \right][/latex]
  8. [latex](0, 1)[/latex]
  9. [latex]\left(-\infty, 1-\frac{\sqrt{6}}{2} \right) \cup \left(1+\frac{\sqrt{6}}{2}, \infty \right)[/latex]
  10. [latex]\left(-\infty, \frac{5 - \sqrt{73}}{6} \right] \cup \left[\frac{5 + \sqrt{73}}{6}, \infty \right)[/latex]
  11. [latex]\left(-3\sqrt{2}, -\sqrt{11} \right] \cup \left[-\sqrt{7}, 0 \right) \cup \left(0, \sqrt{7} \right] \cup \left[\sqrt{11}, 3\sqrt{2} \right)[/latex]
  12. [latex]\left[-2-\sqrt{7}, -2+\sqrt{7} \right] \cup [1, 3][/latex]
  13. [latex](-\infty, \infty)[/latex]
  14. [latex](-\infty, -1] \cup \left\{ 0 \right\} \cup [1,\infty)[/latex]
  15. [latex][-6,-3] \cup [-2, \infty)[/latex]
  16. [latex](-\infty, 1) \cup \left(2, \frac{3+\sqrt{17}}{2}\right)[/latex]
  17. 2 seconds
  18. The rocket reaches its maximum height of 500 feet 10 seconds after lift-off.
  19. The hammer reaches a maximum height of approximately 13.62 feet. The hammer is in the air approximately 1.61 seconds.
  20. .
    1. The applied domain is [latex][0, \infty)[/latex].
    2. Answers May Vary
    3. Answers May Vary
    4. The height function is this case is [latex]s(t) = -4.9t^{2} + 15t[/latex]. The vertex of this parabola is approximately [latex](1.53, 11.48)[/latex] so the maximum height reached by the marble is 11.48 meters. It hits the ground again when [latex]t \approx 3.06[/latex] seconds.
    5. The revised height function is [latex]s(t) = -4.9t^{2} + 15t + 25[/latex] which has zeros at [latex]t \approx -1.20[/latex] and [latex]t \approx 4.26[/latex]. We ignore the negative value and claim that the marble will hit the ground after 4.26 seconds.
    6. Shooting down means the initial velocity is negative so the height functions becomes [latex]s(t) = -4.9t^{2} - 15t + 25.[/latex]
  21. [latex]y = |1 -x^{2}|[/latex]
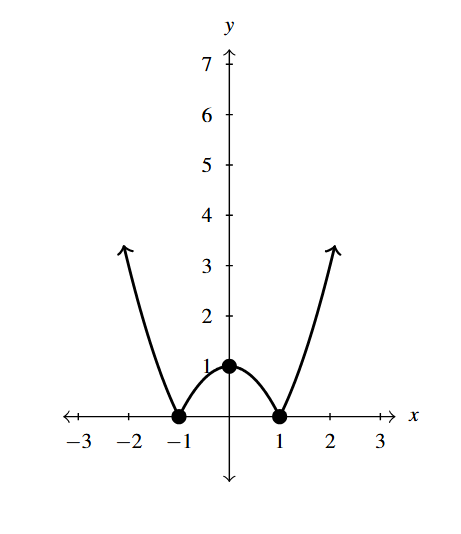
    The rectangular plane with a curve that decreases to (-1,0), increases to (0,1), and then decrease (1,0) and increases after.
    Answer to Exercise 21
  22. [latex]\left(\dfrac{3 - \sqrt{7}}{2}, \dfrac{-1 + \sqrt{7}}{2} \right)[/latex], [latex]\left(\dfrac{3 + \sqrt{7}}{2}, \dfrac{-1 - \sqrt{7}}{2} \right)[/latex]
  23. [latex]D(x) = x^2 + (2x+1)^2 = 5x^2+4x+1[/latex] is minimized when [latex]x=-\frac{2}{5}[/latex]. Hence to find the point on [latex]y=2x+1[/latex] closest to [latex](0,0)[/latex] we substitute [latex]x = -\frac{2}{5}[/latex] into [latex]y=2x+1[/latex] to get [latex]\left(-\frac{2}{5}, \frac{1}{5}\right).[/latex]
  24. [latex]x = -\frac{6}{7}[/latex]
  25. [latex]x = 1, \; x = 2[/latex]
  26. [latex]t = -1[/latex]
  27. [latex]t = -6, \; x = 2[/latex]
  28. No Solution
  29. [latex]z = 0, \; z = \pm 2\sqrt{2}[/latex]
  30. [latex](-2, \infty)[/latex]
  31. [latex](-2, 3][/latex]
  32. [latex](-\infty, -1) \cup (0, 1)[/latex]
  33. [latex][0, \infty)[/latex]
  34. [latex](-\infty, -3) \cup (-3,2) \cup (4, \infty)[/latex]
  35. [latex]\left(-3, -\frac{1}{3} \right) \cup (2,3)[/latex]
  36. [latex](-1,0] \cup (2, \infty)[/latex]
  37. [latex](-\infty, -3) \cup (-2, -1) \cup (1, \infty)[/latex]
  38. [latex](-\infty, 1] \cup [2, \infty)[/latex]
  39. [latex](-\infty, -6) \cup (-1, 2)[/latex]
  40. [latex](-\infty, -3) \cup \left[-2\sqrt{2}, 0\right] \cup \left[2\sqrt{2}, 3\right)[/latex]
  41. No solution.
  42. [latex][-4, -1) \cup (-1,2][/latex]
  43. [latex](-\infty, -6) \cup (-6, -3] \cup [9, \infty)[/latex]
  44. [latex][-3,0) \cup (0,4) \cup [5, \infty)[/latex]
  45. [latex]\left(-1,-\frac{1}{2}\right] \cup (1, \infty)[/latex]
  46. [latex]f(x) \geq 0[/latex] on [latex](-\infty, 0) \cup [3, \infty)[/latex]
  47. [latex]f(x)[/latex] < 1 on [latex](0, \infty)[/latex]
  48. [latex]g(t) \geq -1[/latex] on [latex](-\infty, 1] \cup (2, \infty)[/latex]
  49. [latex]-1 \leq g(t)[/latex] < 1 on [latex](-\infty, 1] \cup (3, \infty)[/latex]
  50. [latex]r(z) \leq 1[/latex] on [latex](-\infty, -1] \cup (1, \infty)[/latex]
  51. [latex]r(z) > 0[/latex] on [latex](-\infty, 0) \cup (0,1) \cup (1, \infty)[/latex]
  52. The absolute minimum of [latex]y=\overline{C}(x)[/latex] occurs at [latex]\approx (75.73, 59.57)[/latex]. Given [latex]x[/latex] represents the number of game systems, we check [latex]\overline{C}(75) \approx 59.58[/latex] and [latex]\overline{C}(76) \approx 59.57[/latex]. Hence, to minimize the average cost, 76 systems should be produced at an average cost of \$59.57 per system.
  53. The width (and depth) should be 10.00 centimeters, the height should be 5.00 centimeters. The minimum surface area is 300.00 square centimeters.
  54. The width of the base of the box should be approximately 4.12 inches, the height of the box should be approximately 6.67 inches, and the depth of the base of the box should be approximately 5.09 inches. The minimum surface area is approximately 164.91 square inches.
  55. The dimensions are approximately 7 feet by 14 feet. Hence the minimum amount of fencing required is approximately 28 feet.
  56. .
    1. [latex]V = \pi r^{2}h[/latex]
    2. [latex]S = 2 \pi r^{2} + 2\pi r h[/latex]
    3. [latex]S(r) = 2\pi r^{2} + \frac{67.2}{r}, \;[/latex] Domain [latex]r > 0[/latex]
    4. [latex]r \approx 1.749\,[/latex]in. and [latex]h \approx 3.498\,[/latex]in.
  57. The radius of the drum should be approximately 1.05 feet and the height of the drum should be approximately 2.12 feet. The minimum surface area of the drum is approximately 20.93 cubic feet.
  58. [latex]P(t)[/latex] < 100 on [latex](-15, 30)[/latex], and the portion of this which lies in the applied domain is [latex][0,30)[/latex]. Given [latex]t=0[/latex] corresponds to the year 1803, from 1803 through the end of 1832, there were fewer than 100 Sasquatch in Portage County.
  59. [latex][-8,8][/latex]
  60. [latex][-1, 0] \cup [1, \infty)[/latex]
  61. [latex]\left(-\infty, \frac{1}{3} \right)[/latex]
  62. [latex]\left[ -\frac{\sqrt{5}}{2}, -1\right) \cup \left(1, \frac{\sqrt{5}}{2}\right][/latex]
  63. [latex]\left(-\infty, -\frac{3\sqrt{2}}{4} \right] \cup (-1,1) \cup \left[ \frac{3\sqrt{2}}{4}, \infty \right)[/latex]
  64. [latex]\left[ \frac{3}{4}, 1\right) \cup (1, \infty)[/latex]
  65. [latex]\left( -\infty, \frac{3}{5} \right] \cup (1, \infty)[/latex]
  66. [latex](-\infty, 2) \cup (2,3][/latex]
  67. [latex](2,6][/latex]
  68. [latex](-\infty, 0) \cup [2,3) \cup (3, \infty)[/latex]
  69. [latex](-\infty, -1)[/latex]
  70. [latex][4,7)[/latex]
  71. [latex]\left(0, \frac{27}{13} \right)[/latex]
  72. [latex](-\infty, 0) \cup (0,3)[/latex]
  73. [latex](-\infty, -4) \cup \left(-4, -\frac{22}{19}\right] \cup (2, \infty)[/latex]

 

  1. You may need to zoom in to see this. ↵
  2. You may need to zoom in to see this. ↵
  3. Note you may need to zoom in to see this. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Functions, Trigonometry, and Systems of Equations (Second Edition) Copyright © 2025 by Texas A&M Mathematics Department is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book