Section 0.1 Answers
- 6
- 0
- \(\dfrac{2}{21}\)
- \( \dfrac{19}{24} \)
- \( -\dfrac{1}{3} \)
- \( -1 \)
- 8
- \(-\dfrac{7}{8} \)
- Undefined
- 0
- Undefined
- \( \dfrac{23}{9} \)
- \( -\dfrac{4}{99} \)
- \(-\dfrac{24}{7} \)
- 0
- \( \dfrac{243}{32} \)
- \( \dfrac{13}{48} \)
- \( \dfrac{9}{22} \)
- \( \dfrac{25}{4}\)
- 5
- \( -3\sqrt{3} \)
- \(\dfrac{107}{27}\)
- \( -\dfrac{3\sqrt[5]{3}}{8} = -\dfrac{3^{6/5}}{8} \)
- \( \sqrt{10} \)
- \( \dfrac{\sqrt{61}}{2} \)
- \( \sqrt{7} \)
- \( \dfrac{-4 + \sqrt{2}}{7}\)
- \(-1\)
- \( 2 + \sqrt{5}\)
- \( \dfrac{15}{16} \)
- 13
- \( -\dfrac{385}{12} \)
- \( 1.38 \times 10^{10237} \)
Section 0.2 Answers
- [latex]3|x|[/latex]
- [latex]2t[/latex]
- [latex]5|y^3|\sqrt{2}[/latex]
- [latex]|2t+1|[/latex]
- [latex]|w-8|[/latex]
- [latex]\sqrt{3x+1}[/latex]
- [latex]\dfrac{\sqrt{c^2-v^2}}{|c|}[/latex]
- [latex]\dfrac{2r \sqrt[3]{3 \pi r^2}}{L}[/latex]
- [latex]\dfrac{2 \varepsilon^2 \sqrt[4]{2\pi}}{|\rho^3|}[/latex]
- [latex]-\dfrac{1}{\sqrt{x}}[/latex]
- [latex]\dfrac{3-6t^2}{\sqrt{1-t^2}}[/latex]
- [latex]\dfrac{6-8z}{3 (\sqrt[3]{1-z})^2}[/latex]
- [latex]\dfrac{4x-3}{(2x-1)\sqrt[3]{2x-1}}[/latex]
Section 0.3 Answers
- [latex]2x(1 - 5x)[/latex]
- [latex]4t^3(3t^2-2)[/latex]
- [latex]4xy(4y-3x)[/latex]
- [latex]-(m+3)^2(4m+7)[/latex]
- [latex](2x-1)(x-1)[/latex]
- [latex](t-5)(t^2+1)[/latex]
- [latex](w-11)(w+11)[/latex]
- [latex](7-2t)(7+2t)[/latex]
- [latex](3t-2)(3t+2)(9t^2+4)[/latex]
- [latex](3z-8y^2)(3z+8y^2)[/latex]
- [latex]-3(y - 3)(y+1)[/latex]
- [latex](x+h)(x+h-1)(x+h+1)[/latex]
- [latex](y-12)^2[/latex]
- [latex](5t+1)^2[/latex]
- [latex]3x(2x-3)^2[/latex]
- [latex](m^2+5)^2[/latex]
- [latex](3-2x)(9 + 6x + 4x^2)[/latex]
- [latex]t^3(t+1)(t^2 - t + 1)[/latex]
- [latex](x-7)(x+2)[/latex]
- [latex](y-9)(y-3)[/latex]
- [latex](3t+1)(t+5)[/latex]
- [latex](2x-5)(3x-4)[/latex]
- [latex](7-m)(5+m)[/latex]
- [latex](-2w+1)(w-3)[/latex]
- [latex]3m(m-1)(m+4)[/latex]
- [latex](x-2)(x+2)(x^2+5)[/latex]
- [latex](2t-3)(2t+3)(t^2+1)[/latex]
- [latex](x-3)(x+3)(x-5)[/latex]
- [latex](t-3)(1-t)(1+t)[/latex]
- [latex](y^2-y+3)(y^2+y+3)[/latex]
Section 0.4 Answers
- [latex]O[/latex] is the odd natural numbers
- [latex]X = \{ 0, 1, 4, 9, 16, \ldots \}[/latex]
- a. [latex]\dfrac{20}{10} = 2[/latex] and 117
b. [latex]\sqrt{3}[/latex] and 5.2020020002
c. [latex]\left\{ -3, \dfrac{20}{10}, 117\right\}[/latex]
d.[latex]\left\{ -3, -1.02, -\dfrac{3}{5}, 0.57, 1.\overline{23},\dfrac{20}{10}, 117 \right \}[/latex] - Completed Table

Answer to Exercise 4 - [latex](-1,5] \cap [0,8) = [0,5][/latex]
- [latex](-1,1) \cup [0,6] = (-1,6][/latex]
- [latex](-\infty,4]\cap (0,\infty) = (0,4][/latex]
- [latex](-\infty,0) \cap [1,5] = \emptyset[/latex]
- [latex](-\infty, 0) \cup [1,5] = (-\infty,0) \cup [1,5][/latex]
- [latex](-\infty, 5] \cap [5,8) = \left\{ 5\right\}[/latex]
- [latex](-\infty, 5) \cup (5, \infty)[/latex]
- [latex](-\infty, -1) \cup (-1, \infty)[/latex]
- [latex](-\infty, -3) \cup (-3, 4)\cup (4, \infty)[/latex]
- [latex](-\infty, 0) \cup (0, 2)\cup (2, \infty)[/latex]
- [latex](-\infty, -2) \cup (-2, 2)\cup (2, \infty)[/latex]
- [latex](-\infty, -4) \cup (-4, 0) \cup (0, 4) \cup (4, \infty)[/latex]
- [latex](-\infty, -1] \cup [1, \infty)[/latex]
- [latex][2, 3)[/latex]
- [latex](-\infty, -3] \cup (0, \infty)[/latex]
- [latex]\emptyset[/latex]
- [latex]\{-1\} \cup \{1\} \cup (2, \infty)[/latex]
- [latex](3,4) \cup (4, 13)[/latex]
- [latex]A \cup C[/latex]
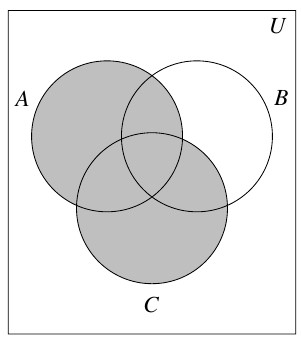
Answer to Exercise 23 - [latex]B \cap C[/latex]
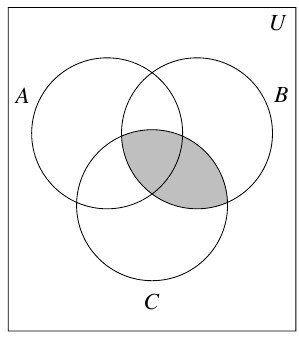
Answer to Exercise 24 - [latex](A \cup B) \cup C[/latex]
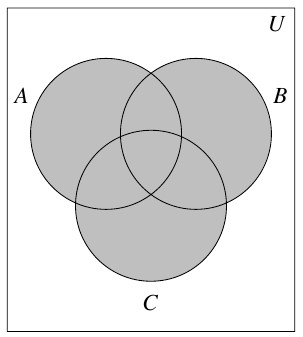
Answer to Exercise 25 - [latex](A \cap B) \cap C[/latex]
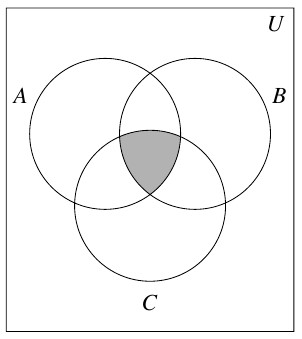
Answer to Exercise 26 - [latex]A \cap (B \cup C)[/latex]
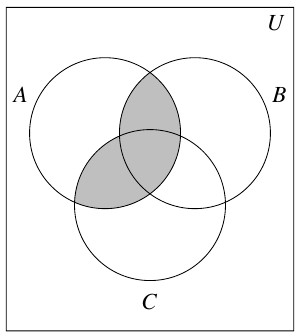
Answer to Exercise 27 - [latex](A \cap B) \cup (A \cap C)[/latex]

Answer to Exercise 28 - Yes, [latex]A \cup (B \cap C) = (A \cup B) \cap (A \cup C)[/latex]
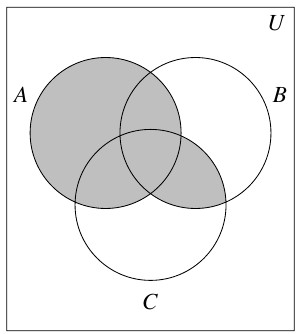
Answer to Exercise 29
Section 0.5 Answers
- [latex]x = \dfrac{18}{7}[/latex]
- [latex]t = -\dfrac{1}{30}[/latex]
- [latex]w = \dfrac{61}{33}[/latex]
- [latex]y = 50000[/latex]
- All real numbers
- No solution
- [latex]t = -\dfrac{5}{3\sqrt{7}} = -\dfrac{5\sqrt{7}}{21}[/latex]
- [latex]y = \dfrac{6}{17\sqrt{2}} = \dfrac{3 \sqrt{2}}{17}[/latex]
- [latex]x = \dfrac{27}{18+\sqrt{7}}[/latex]
- [latex]y = \dfrac{4 - 3x}{2} \text{ or } y = -\dfrac{3}{2}x + 2[/latex]
- [latex]x = \dfrac{4 - 2y}{3} \text{ or } x = -\dfrac{2}{3} y + \dfrac{4}{3}[/latex]
- [latex]C = \dfrac{5}{9}(F - 32) \text{ or } C = \dfrac{5}{9} F - \dfrac{160}{9}[/latex]
- [latex]x = \dfrac{p - 15}{-2.5} = \dfrac{15-p}{2.5} \text{ or } x = -\dfrac{2}{5} p + 6[/latex]
- [latex]x = \dfrac{C - 1000}{200} \text{ or } x = \dfrac{1}{200} C - 5[/latex]
- [latex]y = \dfrac{x-7}{4} \text{ or } y = \dfrac{1}{4} x - \dfrac{7}{4}[/latex]
- [latex]w = \dfrac{3v+1}{v}[/latex], provided [latex]v \neq 0[/latex]
- [latex]v = \dfrac{1}{w-3}[/latex], provided [latex]w \neq 3[/latex]
- [latex]y = \dfrac{3x+1}{x-2}[/latex], provided [latex]x \neq 2[/latex]
- [latex]\pi = \dfrac{C}{2r}[/latex], provided [latex]r \neq 0[/latex]
- [latex]V = \dfrac{nRT}{P}[/latex], provided [latex]P \neq 0[/latex]
- [latex]R = \dfrac{PV}{nT}[/latex], provided [latex]n \neq 0[/latex], [latex]T \neq 0[/latex]
- [latex]g = \dfrac{E}{mh}[/latex], provided [latex]m \neq 0[/latex], [latex]h \neq 0[/latex]
- [latex]m = \dfrac{2E}{v^2}[/latex], provided [latex]v^2 \neq 0[/latex] (so [latex]v \neq 0[/latex])
- [latex]V_{2} = \dfrac{P_{1}V_{1}}{P_{2}}[/latex], provided [latex]P_{2} \neq 0[/latex]
- [latex]t = \dfrac{x - x_{0}}{a},[/latex] provided [latex]a \neq 0[/latex]
- [latex]x = \dfrac{y-y_{0} + mx_{0}}{m} \text{ or } x = x_{0} + \dfrac{y-y_{0}}{m}[/latex], provided [latex]m \neq 0[/latex]
- [latex]T_{1} = \dfrac{mcT_{2} - q}{mc} \text{ or } T_{1} = T_{2} - \dfrac{q}{mc}[/latex] , provided [latex]m \neq 0[/latex], [latex]c \neq 0[/latex]
- [latex]x = -6 \text{ or } x=6[/latex]
- [latex]t = -3 \text{ or } t= \dfrac{11}{3}[/latex]
- [latex]w = -3 \text{ or } w= 11[/latex]
- [latex]y = -1 \text{ or } y= 1[/latex]
- [latex]m=-\dfrac{1}{2} \text{ or } m= \dfrac{1}{10}[/latex]
- No solution
- [latex]x=-3 \text{ or } x= 3[/latex]
- [latex]w = -\dfrac{13}{8} \text{ or } w= \dfrac{53}{8}[/latex]
- [latex]t = \dfrac{\sqrt{2} \pm 2}{3}[/latex]
- [latex]v = -1 \text{ or } v = 0[/latex]
- No solution
- [latex]y = \dfrac{3}{2}[/latex]
- [latex]t = -1 \text{ or } t = 9[/latex]
- [latex]x = -\dfrac{1}{7} \text{ or } x = 1[/latex]
- [latex]y = 0 \text{ or } y = \dfrac{2}{\sqrt{2} - 1}[/latex]
- [latex]x=1[/latex]
- [latex]z = -\dfrac{3}{10}[/latex]
- [latex]w = \dfrac{\sqrt{3} \pm 2}{\sqrt{3} \mp 2}[/latex] See footnote[1]
- [latex]x = -\dfrac{3}{7} \text{ or } x = 5[/latex]
- [latex]t = \dfrac{1}{2} \text{ or } t = -4[/latex]
- [latex]y = \dfrac{5}{3} \text{ or } y = -2[/latex]
- [latex]t = 0 \text{ or } t = 4[/latex]
- [latex]y = -1 \text{ or } y = \dfrac{3}{2}[/latex]
- [latex]x = \dfrac{3}{2} \text{ or } x = \dfrac{7}{4}[/latex]
- [latex]x = 0 \text{ or } x = \pm \dfrac{3}{4}[/latex]
- [latex]w = -\dfrac{5}{2} \text{ or } w = \dfrac{2}{3}[/latex]
- [latex]w=-5 \text{ or } w = -\dfrac{1}{2}[/latex]
- [latex]x=3 \text{ or } x = \pm 4[/latex]
- [latex]t = -1, \; t= -\dfrac{1}{2}, \text{ or } t = 0[/latex]
- [latex]a = \pm 1[/latex]
- [latex]t = -\dfrac{3}{4} \text{ or } t = \dfrac{3}{2}[/latex]
- [latex]x = \dfrac{2}{3}[/latex]
- [latex]y = \pm 3[/latex]
- [latex]x = -\dfrac{3}{2}[/latex]
- [latex]y = -1, \; 2[/latex]
- [latex]t = -\dfrac{\sqrt[3]{3}}{2}[/latex]
- [latex]x = 5[/latex]
- [latex]t = \pm 3 \sqrt{7}[/latex]
- [latex]x=3[/latex]
- [latex]y=-3[/latex]
- [latex]t = -\dfrac{1}{3}, \; \dfrac{2}{3}[/latex]
- [latex]x = \dfrac{5 + \sqrt{57}}{8}[/latex]
- [latex]w = \sqrt{3}[/latex]
- [latex]x = 6[/latex]
- [latex]x = 4[/latex]
- [latex]h = \sqrt[3]{\dfrac{12I}{b}}[/latex]
- [latex]a = \dfrac{2 \sqrt[4]{I_{0}}}{\sqrt[4]{5\sqrt{3}}}[/latex]
- [latex]g = \dfrac{4 \pi^2 L}{T^2}[/latex]
- [latex]v = \dfrac{c \sqrt{L_{0}^2 - L^2}}{L_{0}}[/latex]
- [latex]x = \dfrac{3 \pm \sqrt{5}}{6}[/latex]
- [latex]t = -\dfrac{4}{5}, \; -\dfrac{2}{5}[/latex]
- [latex]y = \pm 1 \text{ or } \pm \sqrt{5}[/latex]
- [latex]x = \dfrac{-1 \pm \sqrt{5}}{2}[/latex]
- [latex]w = -1, \; \dfrac{2}{3}[/latex]
- [latex]y = -2 \pm \sqrt{5}[/latex]
- [latex]z = \dfrac{1 \pm \sqrt{65}}{16}[/latex]
- [latex]v = -3, \; 1[/latex]
- No real solution
- [latex]t = \dfrac{-5 \pm \sqrt{33}}{4}[/latex]
- [latex]x = 0[/latex]
- [latex]y = \dfrac{2 \pm \sqrt{10}}{6}[/latex]
- [latex]w = \pm \sqrt{\dfrac{\sqrt{13} - 3}{2}}[/latex]
- [latex]x = \pm 1[/latex]
- [latex]y = \dfrac{4 \pm \sqrt{6 + 2 \sqrt{13}}}{2}[/latex]
- [latex]x = 0, \; \dfrac{5 \pm \sqrt{17}}{2}[/latex]
- [latex]p = -\dfrac{1}{3}, \; \pm \sqrt{2}[/latex]
- [latex]v = 0, \; \pm \sqrt{2}, \; \pm \sqrt{5}[/latex]
- [latex]y = \dfrac{5\sqrt{2} \pm \sqrt{46}}{2}[/latex]
- [latex]x = \dfrac{\sqrt{2} \pm \sqrt{10}}{2}[/latex]
- [latex]v = -\dfrac{\sqrt{3}}{2}, 2\sqrt{3}[/latex]
- [latex]b = \pm \dfrac{\sqrt{13271}}{50}[/latex]
- [latex]r = \pm \sqrt{\dfrac{37}{\pi}}[/latex]
- [latex]r = \dfrac{-4\sqrt{2} \pm \sqrt{54\pi + 32}}{\pi}[/latex]
- [latex]t = \dfrac{500 \pm 10\sqrt{491}}{49}[/latex]
- [latex]x = \dfrac{99 \pm 6 \sqrt{165}}{13}[/latex]
- [latex]A = \dfrac{-107 \pm 7 \sqrt{70}}{330}[/latex]
- [latex]x = 1, \; 2, \; \dfrac{3 \pm \sqrt{17}}{2}[/latex]
- [latex]x = \pm 1, \; 2 \pm \sqrt{3}[/latex]
- [latex]x = -\dfrac{1}{2}, \; 1, \; 7[/latex]
- The discriminant is: [latex]D = p^2 - 4p^2 = -3p^2[/latex]<0 because [latex]D[/latex]< 0, there are no real solutions.
- [latex]t = \dfrac{v \pm \sqrt{v^2 + 2gh}}{g}[/latex]
- [latex]7i[/latex]
- [latex]3i[/latex]
- [latex]-10[/latex]
- 10
- [latex]-12[/latex]
- 12
- 3
- [latex]-3i[/latex]
- [latex]i^{5} = i^{4} \cdot i = 1 \cdot i = i[/latex]
- [latex]i ^{6} = i^{4} \cdot i^{2} = 1 \cdot (-1) = -1[/latex]
- [latex]i^{7} = i^{4} \cdot i^{3} = 1 \cdot (-i) = -i[/latex]
- [latex]i^{8} = i^{4} \cdot i^{4} = \left(i^{4}\right)^{2} = (1)^{2} =1[/latex]
- [latex]i^{15} = \left(i^{4}\right)^{3} \cdot i^{3} = 1 \cdot (-i) = -i[/latex]
- [latex]i ^{26} = \left(i^{4}\right)^{6} \cdot i^{2} = 1\cdot (-1) = -1[/latex]
- [latex]i^{117} = \left(i^{4}\right)^{29} \cdot i = 1 \cdot i = i[/latex]
- [latex]i ^{304} = \left(i^{4}\right)^{76} = 1^{76} = 1[/latex]
- For [latex]z = 2+3i[/latex] and [latex]w = 4i[/latex]
- [latex]z+w = 2+7i[/latex]
- [latex]zw = -12+8i[/latex]
- [latex]z^2 = -5 + 12i[/latex]
- [latex]\dfrac{1}{z} = \dfrac{2}{13} - \dfrac{3}{13} \, i[/latex]
- [latex]\dfrac{z}{w} = \dfrac{3}{4} - \dfrac{1}{2} \, i[/latex]
- [latex]\dfrac{w}{z} = \dfrac{12}{13} + \dfrac{8}{13} \,i[/latex]
- For [latex]z = 1+i[/latex] and [latex]w=-i[/latex]
- [latex]z+w = 1[/latex]
- [latex]zw = 1-i[/latex]
- [latex]z^2 = 2i[/latex]
- [latex]\frac{1}{z} = \frac{1}{2} - \frac{1}{2} \, i[/latex]
- [latex]\frac{z}{w} = -1+i[/latex]
- [latex]\frac{w}{z} = -\frac{1}{2} - \frac{1}{2} \, i[/latex]
- For [latex]z = i[/latex] and [latex]w = -1+2i[/latex]
- [latex]z+w = -1+3i[/latex]
- [latex]zw = -2-i[/latex]
- [latex]z^2 = -1[/latex]
- [latex]\frac{1}{z} = -i[/latex]
- [latex]\frac{z}{w} = \frac{2}{5} - \frac{1}{5} \, i[/latex]
- [latex]\frac{w}{z} = 2+i[/latex]
- For [latex]z = 4i[/latex] and [latex]w = 2-2i[/latex]
- [latex]z+w = 2+2i[/latex]
- [latex]zw = 8+8i[/latex]
- [latex]z^2 = -16[/latex]
- [latex]\frac{1}{z} = -\frac{1}{4} \,i[/latex]
- [latex]\frac{z}{w} = -1+i[/latex]
- [latex]\frac{w}{z} = -\frac{1}{2} - \frac{1}{2} \,i[/latex]
- For [latex]z = 3-5i[/latex] and [latex]w = 2+7i[/latex]
- [latex]z+w = 5+2i[/latex]
- [latex]zw = 41+11i[/latex]
- [latex]z^2 = -16-30i[/latex]
- [latex]\frac{1}{z} = \frac{3}{34} + \frac{5}{34} \,i[/latex]
- [latex]\frac{z}{w} = -\frac{29}{53} - \frac{31}{53} \, i[/latex]
- [latex]\frac{w}{z} = -\frac{29}{34} + \frac{31}{34} \,i[/latex]
- For [latex]z = -5+i[/latex] and [latex]w = 4+2i[/latex]
- [latex]z+w = -1+3i[/latex]
- [latex]zw = -22-6i[/latex]
- [latex]z^2 = 24-10i[/latex]
- [latex]\frac{1}{z} = -\frac{5}{26} - \frac{1}{26} \,i[/latex]
- [latex]\frac{z}{w} = -\frac{9}{10} + \frac{7}{10} \, i[/latex]
- [latex]\frac{w}{z} = -\frac{9}{13} - \frac{7}{13} \,i[/latex]
- For [latex]z = \sqrt{2} - i\sqrt{2}[/latex] and [latex]w = \sqrt{2} + i\sqrt{2}[/latex]
- [latex]z+w = 2\sqrt{2}[/latex]
- [latex]zw = 4[/latex]
- [latex]z^2 = -4i[/latex]
- [latex]\frac{1}{z} = \frac{\sqrt{2}}{4} + \frac{\sqrt{2}}{4} \,i[/latex]
- [latex]\frac{z}{w} = -i[/latex]
- [latex]\frac{w}{z} = i[/latex]
- For [latex]z = 1 - i\sqrt{3}[/latex] and [latex]w = -1-i\sqrt{3}[/latex]
- [latex]z+w = -2i\sqrt{3}[/latex]
- [latex]zw = -4[/latex]
- [latex]z^2 = -2-2i\sqrt{3}[/latex]
- [latex]\frac{1}{z} = \frac{1}{4} + \frac{\sqrt{3}}{4} \,i[/latex]
- [latex]\frac{z}{w} = \frac{1}{2} + \frac{\sqrt{3}}{2} \,i[/latex]
- [latex]\frac{w}{z} = \frac{1}{2} - \frac{\sqrt{3}}{2} \,i[/latex]
- For [latex]z = \frac{1}{2} + \frac{\sqrt{3}}{2} \, i[/latex] and [latex]w = -\frac{1}{2} + \frac{\sqrt{3}}{2} \,i[/latex]
- [latex]z+w = i\sqrt{3}[/latex]
- [latex]zw = -1[/latex]
- [latex]z^2 = -\frac{1}{2} + \frac{\sqrt{3}}{2} \,i[/latex]
- [latex]\frac{1}{z} = \frac{1}{2} - \frac{\sqrt{3}}{2} \, i[/latex]
- [latex]\frac{z}{w} = \frac{1}{2} - \frac{\sqrt{3}}{2} \, i[/latex]
- [latex]\frac{w}{z} = \frac{1}{2} + \frac{\sqrt{3}}{2} \, i[/latex]
- For [latex]z = -\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} \, i[/latex] and [latex]w = -\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} \, i[/latex]
- [latex]z + w = -\sqrt{2}[/latex]
- [latex]zw = 1[/latex]
- [latex]z^2 =-i[/latex]
- \frac{1}{z} = -\frac{\sqrt{2}}{2} – \frac{\sqrt{2}}{2} \, i
- [latex]\frac{z}{w} = -i[/latex]
- [latex]\frac{w}{z} = i[/latex]
- [latex]x = \dfrac{2 \pm i\sqrt{14}}{3}[/latex]
- [latex]t = 5, \; \pm \dfrac{i \sqrt{3}}{3}[/latex]
- [latex]y = \pm 2, \; \pm i[/latex]
- [latex]w = \dfrac{1 \pm i \sqrt{7}}{2}[/latex]
- [latex]y = \pm \dfrac{3i \sqrt{2}}{2}[/latex]
- [latex]x= 0, \; \dfrac{1 \pm i\sqrt{2}}{3}[/latex]
- [latex]x = \dfrac{\sqrt{5} \pm i\sqrt{3}}{2}[/latex]
- [latex]y = \pm i, \; \pm \dfrac{i\sqrt{2}}{2}[/latex]
- [latex]z = \pm 2, \; \pm 2i[/latex]
Section 0.6 Answers
- [latex]\left(-\infty, \dfrac{3}{4}\right][/latex]
- [latex]\left(-\infty, \dfrac{7}{6} \right)[/latex]
- [latex]\left( -\infty, \dfrac{3}{13}\right][/latex]
- [latex]\left(-\dfrac{4}{3}, \infty\right)[/latex]
- No solution
- [latex](-\infty, \infty)[/latex]
- [latex](4, \infty)[/latex]
- [latex]\left[ \dfrac{7}{2 - \sqrt[3]{18}}, \infty\right)[/latex]
- [latex][0, \infty)[/latex]
- [latex]\left[ \dfrac{1}{2}, \dfrac{7}{10}\right][/latex]
- [latex]\left(-\dfrac{23}{6}, \dfrac{19}{2} \right][/latex]
- [latex]\left(-\dfrac{13}{10}, -\dfrac{7}{10} \right][/latex]
- [latex](-4,1][/latex]
- [latex]\{1 \} = [1,1][/latex]
- [latex]\left[-6, \dfrac{18}{19} \right)[/latex]
- [latex](-\infty, -1] \cup [0, \infty)[/latex]
- [latex](-\infty, -7) \cup [4, \infty)[/latex]
- [latex](-\infty, \infty)[/latex]
- \left[\dfrac{1}{3}, 3\right]
- [latex]\left(-\infty, -\dfrac{12}{7} \right) \cup \left(\dfrac{8}{7}, \infty\right)[/latex]
- [latex](-3,2)[/latex]
- [latex](-\infty,1] \cup [3,\infty)[/latex]
- No solution
- [latex](-\infty, \infty)[/latex]
- [latex](-\infty, -6-\sqrt{5}) \cup (6-\sqrt{5}, \infty)[/latex]
- [latex]\left[ -\dfrac{3}{4}, \dfrac{3}{4}\right][/latex]
- No solution
- [latex](-3,2] \cup [6,11)[/latex]
- [latex][3, 4) \cup (5, 6][/latex]
- [latex]\left(\dfrac{2 \sqrt{3} - 3}{2}, \dfrac{2 \sqrt{3} - 1}{2} \right) \cup \left(\dfrac{2 \sqrt{3} +1}{2}, \dfrac{2 \sqrt{3} +3}{2} \right)[/latex]
- That is, [latex]w = \dfrac{\sqrt{3} + 2}{\sqrt{3} - 2}[/latex] or [latex]w = \dfrac{\sqrt{3} - 2}{\sqrt{3} + 2}[/latex] ↵

